Matrix complement refers to the matrix formed by replacing each element with its corresponding minor or cofactor, which is essential for calculating the inverse of a square matrix. Understanding matrix complements allows you to solve systems of linear equations, compute determinants, and perform advanced linear algebra operations crucial in engineering and computer science. Explore the rest of the article to master how matrix complements simplify complex matrix computations.
Table of Comparison
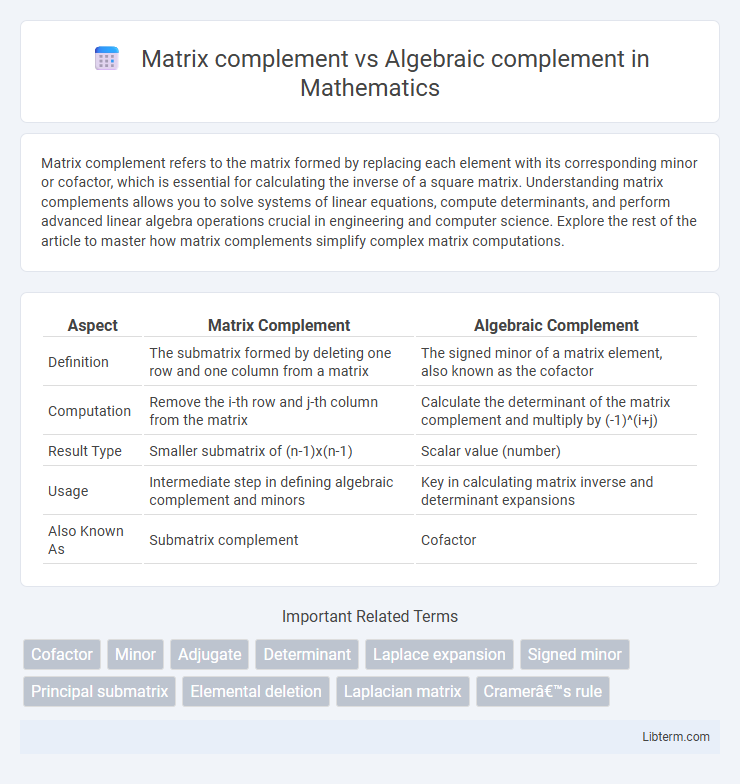
| Aspect | Matrix Complement | Algebraic Complement |
|---|---|---|
| Definition | The submatrix formed by deleting one row and one column from a matrix | The signed minor of a matrix element, also known as the cofactor |
| Computation | Remove the i-th row and j-th column from the matrix | Calculate the determinant of the matrix complement and multiply by (-1)^(i+j) |
| Result Type | Smaller submatrix of (n-1)x(n-1) | Scalar value (number) |
| Usage | Intermediate step in defining algebraic complement and minors | Key in calculating matrix inverse and determinant expansions |
| Also Known As | Submatrix complement | Cofactor |
Introduction to Matrix Complement and Algebraic Complement
Matrix complement refers to the process of creating a submatrix by deleting a specific row and column from a given matrix, often called the minor associated with that element. Algebraic complement, or cofactor, extends this by applying a sign factor \((-1)^{i+j}\) to the minor, where \(i\) and \(j\) are the row and column indices, respectively, crucial for determinant expansion. Understanding both concepts is fundamental in matrix theory, particularly when calculating determinants, inverses, and solving linear systems.
Defining Matrix Complement: Key Concepts
Matrix complement refers to the submatrix formed by removing the specified row and column from the original matrix, commonly used to calculate the determinant and inverse. Algebraic complement, or cofactor, incorporates the matrix complement with a sign factor based on the position (-1)^(i+j), crucial for determinant expansion along rows or columns. Understanding the difference is essential in computations involving minors, cofactors, and adjugate matrices in linear algebra.
Algebraic Complement: Meaning and Importance
The algebraic complement, also known as the cofactor, is a crucial concept in matrix theory used to calculate determinants and inverses of square matrices. It is defined as (-1)^(i+j) times the determinant of the submatrix obtained by removing the i-th row and j-th column, playing a key role in Laplace expansion. Understanding algebraic complements enables efficient computation of matrix inverses and solutions to systems of linear equations, highlighting its importance in linear algebra and applied mathematics.
Mathematical Formulation of Matrix Complement
The matrix complement, often called the complement matrix, is formed by replacing each element with its corresponding cofactor, which involves the determinant of the submatrix obtained by removing the element's row and column, combined with a sign factor (-1)^{i+j}. This contrasts with the algebraic complement, synonymous with the cofactor itself, emphasizing the determinant calculation and sign without constructing a full matrix. Mathematically, the matrix complement C of an nxn matrix A is defined as C_{ij} = (-1)^{i+j} \det(M_{ij}), where M_{ij} is the minor of element a_{ij}.
How Algebraic Complement is Calculated
The algebraic complement, also known as the cofactor, of an element in a matrix is calculated by first determining the minor, which is the determinant of the submatrix formed by deleting the element's row and column. This minor is then multiplied by (-1) raised to the power of the sum of the element's row and column indices, ensuring the correct sign. The resulting value is the algebraic complement used in various matrix operations such as finding the adjugate or inverse of a matrix.
Differences Between Matrix Complement and Algebraic Complement
Matrix complement refers to the submatrix obtained by removing a specific row and column from a given matrix, whereas algebraic complement, also known as cofactor, is the matrix complement multiplied by (-1)^(i+j), where i and j denote the row and column indices. The algebraic complement is used in determinant expansion and inverse matrix calculations, incorporating a sign factor that the matrix complement lacks. Unlike the pure submatrix structure of the matrix complement, the algebraic complement carries both the minor determinant value and the alternating sign necessary for cofactor matrices.
Applications of Matrix Complement in Linear Algebra
Matrix complement, often referred to as the cofactor matrix, plays a critical role in calculating the inverse of a square matrix by providing the adjugate matrix necessary for the formula \( A^{-1} = \frac{1}{\det(A)} \text{adj}(A) \). This concept is fundamental in solving systems of linear equations through Cramer's rule, where determinants of minors and their complements determine variable values. The algebraic complement, used interchangeably with cofactors, simplifies eigenvalue computations and facilitates matrix decompositions critical for numerical linear algebra applications.
Uses of Algebraic Complement in Determinant Calculation
Algebraic complements, also known as cofactors, play a crucial role in determinant calculation by enabling the expansion of a matrix's determinant along a row or column. Each algebraic complement is the signed minor of the matrix element, facilitating the recursive breakdown of large matrices into smaller submatrices for easier determinant evaluation. This method is fundamental in linear algebra for solving systems of equations, finding matrix inverses, and analyzing matrix properties.
Common Mistakes in Interpreting Complements
Matrix complement often confuses with algebraic complement, but these concepts differ significantly in linear algebra--matrix complement refers to the submatrix formed by deleting specific rows and columns, while algebraic complement (cofactor) includes a sign factor based on the position of the element. Common mistakes arise when ignoring the sign when calculating cofactors, leading to incorrect determinants or inverse matrices. Another frequent error is applying the matrix complement in contexts that require algebraic complements, resulting in wrong values during matrix expansions or inversions.
Summary: Matrix Complement vs Algebraic Complement
Matrix complement refers to the submatrix formed by removing a specific row and column from a larger matrix, used in the calculation of minors. Algebraic complement, or cofactor, builds on this by assigning a sign based on the position of the element, calculated as (-1)^(i+j) times the matrix complement's determinant. Understanding the distinction is crucial for computing determinants and inverses in linear algebra.
Matrix complement Infographic
 libterm.com
libterm.com