A branched cover is a mathematical concept describing a continuous surjective map between topological spaces that is locally homeomorphic except over a discrete subset known as branch points. Understanding branched covers is essential in fields like complex analysis, algebraic geometry, and topology because they reveal intricate structures of surfaces and spaces. Explore the article to uncover the fascinating properties and applications of branched covers.
Table of Comparison
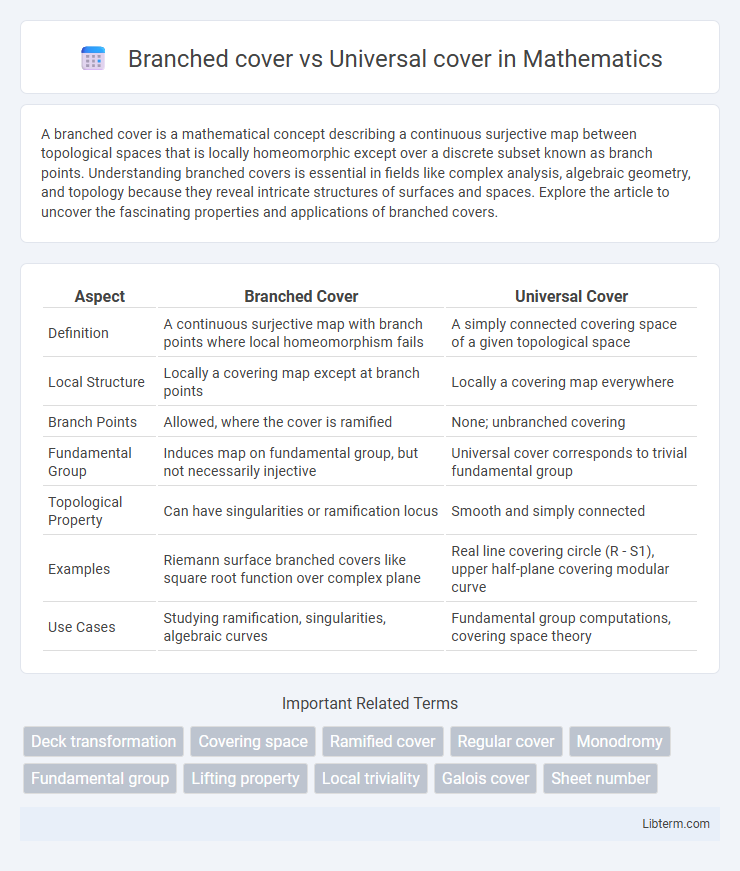
| Aspect | Branched Cover | Universal Cover |
|---|---|---|
| Definition | A continuous surjective map with branch points where local homeomorphism fails | A simply connected covering space of a given topological space |
| Local Structure | Locally a covering map except at branch points | Locally a covering map everywhere |
| Branch Points | Allowed, where the cover is ramified | None; unbranched covering |
| Fundamental Group | Induces map on fundamental group, but not necessarily injective | Universal cover corresponds to trivial fundamental group |
| Topological Property | Can have singularities or ramification locus | Smooth and simply connected |
| Examples | Riemann surface branched covers like square root function over complex plane | Real line covering circle (R - S1), upper half-plane covering modular curve |
| Use Cases | Studying ramification, singularities, algebraic curves | Fundamental group computations, covering space theory |
Introduction to Covering Spaces
Covering spaces are continuous surjective maps where each point in the base space has a neighborhood evenly covered by the cover. Branched covers generalize this concept by allowing certain singularities or branch points where local homeomorphism fails. Universal covers are special covering spaces that are simply connected and cover the entire topological space, serving as foundational tools for studying fundamental groups and lifting properties.
Definition of Branched Covers
A branched cover is a continuous surjective map between topological spaces, typically between surfaces, that is locally modeled on the complex power map \( z \mapsto z^n \), allowing for defined branch points where the map fails to be a local homeomorphism. Unlike universal covers, branched covers accommodate ramification points with specific branching orders, making them crucial in complex analysis and algebraic geometry to study ramified coverings. The local structure near a branch point is characterized by a branching index, which quantifies the degree of ramification and dictates how sheets of the cover come together.
Definition of Universal Covers
Universal covers are simply connected covering spaces that map onto a given topological space, serving as the most extensive and fundamental type of covering. Unlike branched covers, which allow branching points where the cover fails to be locally homeomorphic, universal covers maintain a locally homeomorphic relationship everywhere. These covers are essential in algebraic topology for studying the fundamental group and lifting properties of maps.
Key Differences Between Branched and Universal Covers
Branched covers include branch points where the covering map fails to be locally homeomorphic, often resulting in singularities, whereas universal covers are simply connected spaces that cover the base space without branch points. Universal covers are unique up to isomorphism and serve as the maximal covering space, while branched covers can have multiple distinct forms depending on branching configurations. The fundamental group acts trivially on universal covers but can have more complex actions on branched covers due to the presence of branching.
Examples of Branched Covers in Topology
Branched covers in topology often arise in complex analysis, such as the map \( f(z) = z^n \) from the complex plane to itself, which branches at \( z=0 \). Another key example is the Riemann surface of the square root function, acting as a two-sheeted branched cover of the complex plane with a branch point at the origin. Unlike universal covers, branched covers allow for controlled singularities at branch points, leading to rich structures in algebraic topology and complex geometry.
Examples of Universal Covers in Topology
The universal cover of a topological space is a simply connected covering space that maps onto the original space, such as the real line \(\mathbb{R}\) covering the circle \(S^1\) or the complex plane \(\mathbb{C}\) covering the punctured complex plane \(\mathbb{C} \setminus \{0\}\). Branched covers differ by allowing branch points where the local homeomorphism condition fails, exemplified by the Riemann surface of the square root function acting as a branched cover over \(\mathbb{C}\). Universal covers are fundamental in studying fundamental groups and are used extensively in classifying surfaces and analyzing fiber bundles.
Applications of Branched Covers
Branched covers play a crucial role in complex analysis and algebraic geometry by enabling the study of ramified maps and singularities, particularly in constructing Riemann surfaces and analyzing algebraic curves. They are extensively applied in topology for modeling multi-valued functions and resolving branch points, which aids in understanding monodromy and fundamental group actions. In contrast to universal covers, branched covers provide a more flexible framework for examining local behavior around critical points and facilitate applications in string theory and branched complex surfaces.
Applications of Universal Covers
Universal covers provide a powerful tool in algebraic topology by simplifying complex spaces into simply connected ones, enabling the study of fundamental groups and covering space theory. They are essential in classifying covering spaces, analyzing fiber bundles, and resolving problems in differential geometry, such as lifting geometric structures and studying Riemann surfaces. Compared to branched covers, universal covers avoid singularities, making them ideal for homotopy theory, complex analysis, and geometric group theory applications.
Relationships and Interactions Between Branched and Universal Covers
The universal cover of a topological space is a simply connected, unbranched covering space, serving as a canonical lifting space for all other covers, whereas branched covers introduce singularities by allowing branching points where local homeomorphism fails. Branched covers can often be viewed as quotients of the universal cover by a subgroup of the fundamental group acting with fixed points, reflecting how branching corresponds to fixed points under group actions on the universal cover. Understanding this relationship is crucial for studying the interplay between algebraic properties of the fundamental group and the geometric structure of covers, particularly in complex analysis and algebraic geometry contexts.
Summary and Future Directions
Branched covers generalize universal covers by allowing specified branch points where the covering map fails to be locally homeomorphic, enabling the study of spaces with singularities or branching behavior. Universal covers are simply connected spaces that cover a given space without branching, playing a crucial role in classifying fundamental groups and topological properties. Future research will likely explore higher-dimensional branched covers, applications in complex geometry and topology, and their interplay with modern algebraic and geometric structures.
Branched cover Infographic
 libterm.com
libterm.com