Borel sets form the foundation of modern measure theory and are generated through open sets by applying countable unions, countable intersections, and complements. These sets play a crucial role in defining measurable spaces, enabling rigorous integration and probability theory. Dive deeper into the properties and applications of Borel sets in the rest of this article.
Table of Comparison
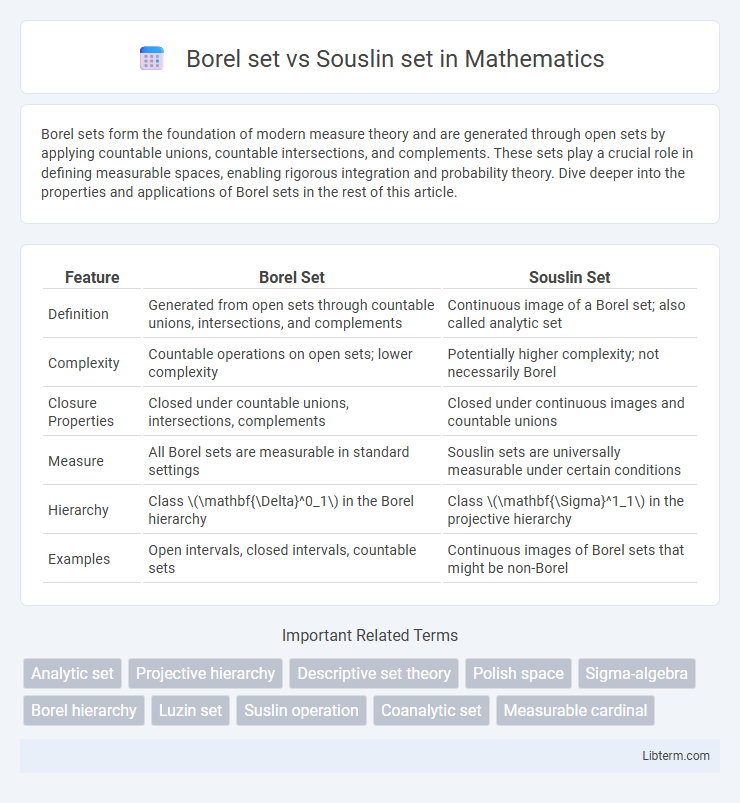
| Feature | Borel Set | Souslin Set |
|---|---|---|
| Definition | Generated from open sets through countable unions, intersections, and complements | Continuous image of a Borel set; also called analytic set |
| Complexity | Countable operations on open sets; lower complexity | Potentially higher complexity; not necessarily Borel |
| Closure Properties | Closed under countable unions, intersections, complements | Closed under continuous images and countable unions |
| Measure | All Borel sets are measurable in standard settings | Souslin sets are universally measurable under certain conditions |
| Hierarchy | Class \(\mathbf{\Delta}^0_1\) in the Borel hierarchy | Class \(\mathbf{\Sigma}^1_1\) in the projective hierarchy |
| Examples | Open intervals, closed intervals, countable sets | Continuous images of Borel sets that might be non-Borel |
Introduction to Borel and Souslin Sets
Borel sets form the smallest s-algebra generated by open sets in a topological space, crucial for measure theory and descriptive set theory. Souslin sets, also known as analytic sets, extend Borel sets as continuous images of Polish spaces, exhibiting more complex structure beyond Borel hierarchy. Both Borel and Souslin sets play key roles in classification problems and provide foundational frameworks in modern analysis.
Defining Borel Sets: Basics and Examples
Borel sets form the smallest s-algebra containing all open sets in a given topological space, making them fundamental in measure theory and real analysis. They are generated through countable operations of union, intersection, and complement applied to open sets, producing a hierarchy known as the Borel hierarchy. Classic examples include open intervals, closed intervals, and countable unions of such intervals in the real line, which illustrate the practical construction of Borel sets.
Understanding Souslin Sets: The Analytic Perspective
Souslin sets, also known as analytic sets, extend beyond Borel sets by encompassing continuous images of Borel sets, thereby capturing more complex structures in descriptive set theory. While Borel sets are generated through countable operations on open or closed sets, Souslin sets are defined using projections of Borel sets in product spaces, highlighting their role in the analytic hierarchy. Understanding the analytic perspective of Souslin sets is crucial for grasping their significance in measure theory and real analysis, especially in contexts where classical Borel measurability fails to capture intricate set properties.
Construction Methods: Borel vs Souslin Sets
Borel sets are constructed through countable operations of union, intersection, and complement starting from open sets, forming the smallest s-algebra containing all open sets. Souslin sets, or analytic sets, arise as continuous images of Borel sets, often defined via projections of Borel sets in product spaces, which can lead to more complex structures not necessarily Borel. The key construction difference lies in Borel sets being generated through explicit operations on open sets, while Souslin sets involve projection and continuous mappings, extending beyond the Borel hierarchy.
Hierarchy and Classification: Where Borel and Souslin Sets Fit
Borel sets form a fundamental class within the projective hierarchy, generated from open sets through countable unions, intersections, and complements, placing them at the lowest level of complexity in descriptive set theory. Souslin sets, also known as analytic sets, arise as continuous images of Borel sets, extending beyond Borel while remaining definable within the broader projective hierarchy. The distinction highlights the classification: all Borel sets are Souslin, but not all Souslin sets are Borel, marking a critical boundary between the Borel hierarchy and the more complex analytic sets.
Key Properties: Separability, Measurability, and Polish Spaces
Borel sets, generated from open sets through countable unions and intersections, are universally measurable and form a sigma-algebra within Polish spaces, ensuring separability and completeness. Souslin sets, also known as analytic sets, extend Borel sets by being continuous images of Borel sets from Polish spaces, preserving measurability but not necessarily being Borel or separable. Both sets play crucial roles in descriptive set theory, with Souslin sets bridging the gap between Borel complexity and measurable structures in separable complete metric spaces.
Relationships: How Souslin Sets Extend Borel Sets
Souslin sets, also known as analytic sets, extend Borel sets by including all continuous images of Borel sets, thereby encompassing a broader class in descriptive set theory. While every Borel set is Souslin, the converse is not true, as Souslin sets can represent more complex structures beyond the countable operations defining Borel sets. This extension allows Souslin sets to capture intricate measurable phenomena not accessible within the Borel hierarchy, which is crucial in advanced measure theory and real analysis.
Applications in Descriptive Set Theory
Borel sets serve as the foundational class of definable sets in descriptive set theory, essential for analyzing measurable and topological properties within Polish spaces. Souslin sets, also known as analytic sets, extend beyond Borel sets by representing continuous images of Borel sets, enabling the study of more complex definability and hierarchy in projective sets. Applications in descriptive set theory leverage Souslin sets to investigate regularity properties like measurability and the perfect set property, crucial for classifying definable sets and functions in real analysis and effective descriptive set theory.
Notable Theorems Involving Borel and Souslin Sets
The Souslin theorem establishes that every Borel set in a Polish space is also a Souslin set, while conversely, every Souslin set is analytic but not necessarily Borel. The Luzin separation theorem states that disjoint analytic sets can be separated by Borel sets, highlighting the interplay between these classes. Furthermore, the Suslin operation (A-operation) constructs Souslin sets from families of Borel sets, demonstrating their complexity within descriptive set theory.
Summary: Practical Differences and Theoretical Significance
Borel sets, generated from open sets through countable unions and intersections, form the foundation of classical measure theory, ensuring well-defined measurability and topological properties. Souslin sets, also called analytic sets, extend beyond Borel sets by including continuous images of Borel sets, playing a critical role in descriptive set theory and enabling analysis of more complex, non-Borel measurable sets. The practical difference lies in the broader expressive power of Souslin sets for modeling intricate structures, while Borel sets provide a more tractable framework for standard measurable spaces.
Borel set Infographic
 libterm.com
libterm.com