A filtered limit is a concept in category theory that generalizes limits by considering diagrams indexed over filtered categories, ensuring the existence of compatible cones in directed systems. This notion plays a crucial role in areas like algebra, topology, and computer science by enabling the construction of objects that capture the essence of infinite processes or structures. Explore the rest of the article to understand how filtered limits impact various mathematical frameworks and your applications.
Table of Comparison
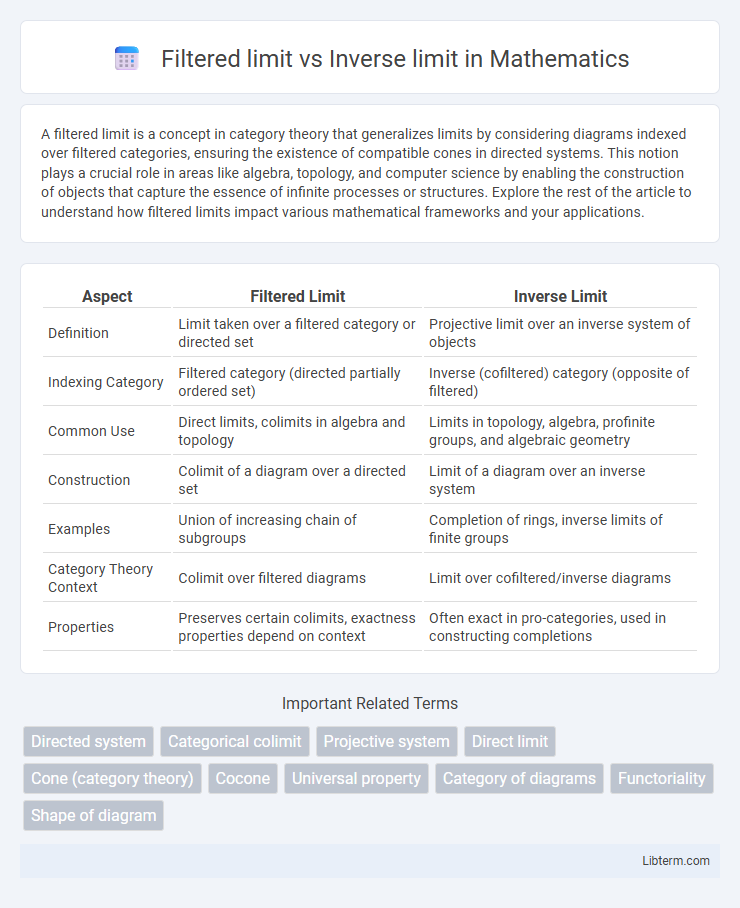
| Aspect | Filtered Limit | Inverse Limit |
|---|---|---|
| Definition | Limit taken over a filtered category or directed set | Projective limit over an inverse system of objects |
| Indexing Category | Filtered category (directed partially ordered set) | Inverse (cofiltered) category (opposite of filtered) |
| Common Use | Direct limits, colimits in algebra and topology | Limits in topology, algebra, profinite groups, and algebraic geometry |
| Construction | Colimit of a diagram over a directed set | Limit of a diagram over an inverse system |
| Examples | Union of increasing chain of subgroups | Completion of rings, inverse limits of finite groups |
| Category Theory Context | Colimit over filtered diagrams | Limit over cofiltered/inverse diagrams |
| Properties | Preserves certain colimits, exactness properties depend on context | Often exact in pro-categories, used in constructing completions |
Introduction to Filtered Limits and Inverse Limits
Filtered limits generalize inverse limits by indexing over filtered categories, enabling the construction of objects as limits of diagrams with directed structures, often used in category theory and algebra. Inverse limits specifically involve diagrams indexed by inverse systems, typically directed sets with a partial order, facilitating the assembly of complex objects from simpler pieces via projections. Both concepts are essential in topology, algebra, and logic for understanding the convergence and coherence of structured data across varying indices.
Definitions: What Are Filtered Limits?
Filtered limits, also known as filtered colimits, are limits taken over a filtered category, where every finite diagram has a cone, ensuring the directedness of the index category. These limits generalize direct limits by allowing the indexing by a category with coherently compatible morphisms, enabling constructions like colimits of directed systems of objects in categories such as sets, groups, or modules. In contrast, inverse limits are limits over inverse (or cofiltered) categories, capturing projective systems and enabling the definition of objects as limits of their finite approximations.
Understanding Inverse Limits
Inverse limits provide a powerful framework in category theory and algebra to construct objects from an inverse system of spaces or algebraic structures connected by bonding maps. Filtered limits refer to limits taken over filtered categories, where any finite subset of objects has an upper bound, ensuring consistency and convergence of directed systems. Understanding inverse limits hinges on grasping how these limits represent the universal object receiving compatible morphisms from all objects in the system, enabling reconstruction of complex structures from simpler, interrelated components.
Key Differences Between Filtered and Inverse Limits
Filtered limits generalize inverse limits by focusing on diagrams indexed over filtered categories, ensuring the existence of cocones over finite subsets, while inverse limits specifically consider diagrams indexed by directed posets emphasizing projective systems. Filtered limits capture colimit-like constructions in categories with filtered diagrams, guaranteeing universal properties related to cones, whereas inverse limits characterize limits over inverse systems, often used in topological and algebraic contexts for capturing projective consistency conditions. The key difference lies in their indexing categories and universality: filtered limits apply to filtered categories facilitating more general co-cones, whereas inverse limits rely on directed posets enforcing an order structure essential for defining projections.
Structural Properties of Filtered Limits
Filtered limits preserve finite limits and commute with finite products in categories such as Set, ensuring structural stability when dealing with diagrams indexed by filtered categories. They are exact in categories like the category of modules, meaning they preserve finite limits and finite colimits, which contrasts with inverse limits that may fail to preserve certain colimits and exactness properties. The structural properties of filtered limits facilitate their use in algebraic contexts for constructing colimits with well-behaved morphisms, supporting coherence and preservation of algebraic structures.
Structural Properties of Inverse Limits
Inverse limits in category theory exhibit strong structural coherence by preserving completeness and compactness properties under appropriate conditions, unlike filtered limits which primarily guarantee the preservation of filtered colimits. The structural properties of inverse limits, especially in topological and algebraic contexts, ensure that complex objects can be reconstructed from simpler approximations with consistent morphisms, maintaining continuity and limit stability. This framework allows inverse limits to effectively capture projective systems' intricate internal symmetries and convergence behaviors, a feature indispensable in many advanced mathematical constructions such as profinite groups and complete local rings.
Examples: Filtered Limit in Category Theory
Filtered limits in category theory often appear in the context of directed systems, such as the direct limit of modules indexed by a filtered poset, exemplified by the construction of colimits in the category of modules. For example, the filtered limit of a diagram of sets indexed by a filtered category corresponds to the direct limit, capturing the notion of coherently combining objects along directed systems. Inverse limits, contrastingly, arise from diagrams indexed by cofiltered categories, such as the inverse limit of projective systems of topological spaces or groups, reflecting limits over systems where morphisms reverse direction.
Examples: Inverse Limit in Category Theory
Inverse limits in category theory assemble objects and morphisms from a directed system into a universal object, exemplified by the inverse limit of a sequence of groups with bonding homomorphisms. Filtered limits generalize inverse limits by allowing indexing over filtered categories rather than just directed posets, capturing more complex diagrams such as those encountered in sheaf theory. An example is the inverse limit of inverse systems of topological spaces, where the limit space inherits the projective topology making it a universal cone over the diagram.
Applications of Filtered and Inverse Limits
Filtered limits are extensively applied in algebraic geometry and homological algebra to construct and analyze objects like sheaves and modules through directed systems, enabling the study of properties preserved under direct limits. Inverse limits primarily facilitate the reconstruction of complex topological or algebraic structures from simpler approximations, crucial in areas such as profinite groups, p-adic number theory, and completion techniques in commutative algebra. The interplay between filtered and inverse limits allows mathematicians to navigate between direct system constructions and inverse system decompositions, enhancing tools for understanding continuity, convergence, and exactness in advanced mathematical frameworks.
Conclusion: Choosing Between Filtered and Inverse Limits
Filtered limits provide a flexible framework to study objects via their directed systems, making them ideal for constructing colimits in categories like sets, groups, or topological spaces. Inverse limits, or projective limits, specialize in capturing the intersection of compatible data across a cofiltered system, often used in algebraic geometry and topology for completeness and compactness properties. Selecting between filtered and inverse limits depends on whether one needs to aggregate data (filtered colimits) or consolidate constraints (inverse limits) within a categorical or algebraic context.
Filtered limit Infographic
 libterm.com
libterm.com