A metrizable space is a topological space that can be endowed with a metric, allowing the topology to be derived from the distance function. This concept plays a critical role in analysis and topology, connecting abstract spaces with more intuitive geometric structures. Explore the rest of the article to understand how metrizable spaces impact continuity, convergence, and compactness in mathematics.
Table of Comparison
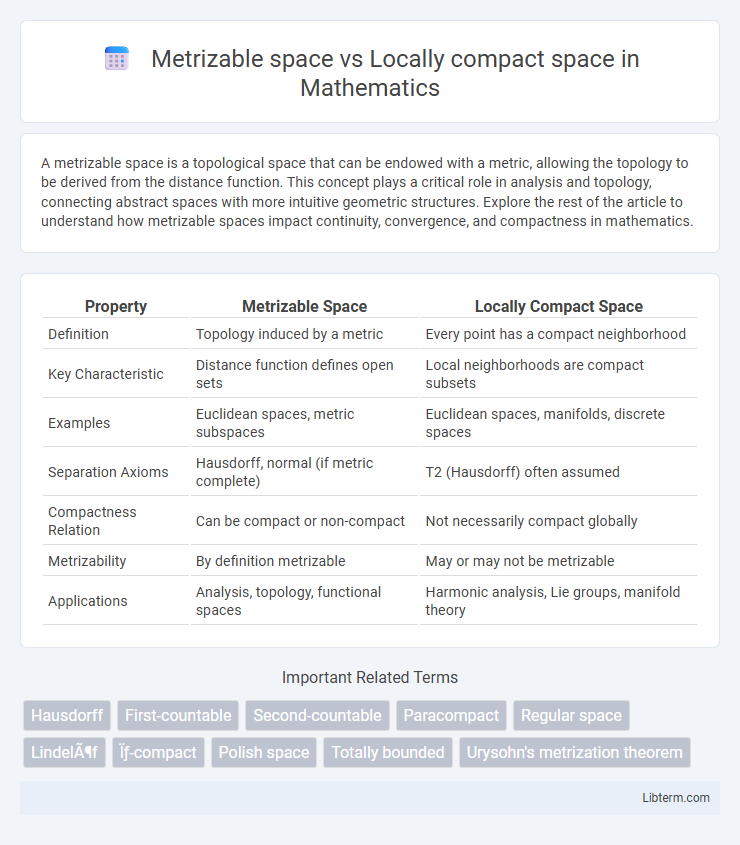
| Property | Metrizable Space | Locally Compact Space |
|---|---|---|
| Definition | Topology induced by a metric | Every point has a compact neighborhood |
| Key Characteristic | Distance function defines open sets | Local neighborhoods are compact subsets |
| Examples | Euclidean spaces, metric subspaces | Euclidean spaces, manifolds, discrete spaces |
| Separation Axioms | Hausdorff, normal (if metric complete) | T2 (Hausdorff) often assumed |
| Compactness Relation | Can be compact or non-compact | Not necessarily compact globally |
| Metrizability | By definition metrizable | May or may not be metrizable |
| Applications | Analysis, topology, functional spaces | Harmonic analysis, Lie groups, manifold theory |
Introduction to Metrizable and Locally Compact Spaces
Metrizable spaces are topological spaces that possess a metric inducing their topology, allowing the use of distance-based tools for analysis and convergence. Locally compact spaces are those in which every point has a compact neighborhood, facilitating the application of compactness properties in local contexts. Understanding the distinction between metrizability and local compactness is essential for studying continuity, convergence, and compactification in topology.
Definition of Metrizable Spaces
Metrizable spaces are topological spaces that can be endowed with a metric inducing their topology, meaning there exists a distance function satisfying positivity, symmetry, and the triangle inequality which defines open sets matching the original topology. Locally compact spaces, by contrast, have the property that every point has a neighborhood whose closure is compact, but they do not necessarily admit a metric. The key distinction is that metrizable spaces guarantee a compatible metric structure, facilitating concrete distance measurements, whereas local compactness pertains to compactness properties in neighborhoods without implying metrizability.
Definition of Locally Compact Spaces
Locally compact spaces are topological spaces in which every point has a neighborhood whose closure is compact, ensuring local compactness around each element. Metrizable spaces are topological spaces that can be endowed with a metric inducing the given topology. Unlike metrizable spaces, locally compact spaces emphasize the existence of compact neighborhoods rather than a metric structure.
Key Properties of Metrizable Spaces
Metrizable spaces are topological spaces that possess a metric inducing their topology, characterized by properties such as being Hausdorff, first-countable, and paracompact. They exhibit crucial features like separability, completeness (when the metric is complete), and the Urysohn metrization theorem applicability, ensuring that every regular second-countable space is metrizable. In contrast, locally compact spaces have local bases of compact neighborhoods but may not be metrizable unless additional conditions, such as second countability, are satisfied.
Key Properties of Locally Compact Spaces
Locally compact spaces are characterized by every point having a compact neighborhood, which guarantees important properties such as the existence of local bases consisting of compact sets and the ability to apply the Riesz representation theorem in analysis. Unlike metrizable spaces, which are defined by the presence of a metric inducing the topology, locally compact spaces emphasize local compactness that facilitates techniques in measure theory and harmonic analysis. This local compactness often ensures that the space can be embedded into a compact Hausdorff space, enabling the use of powerful compactness arguments not always available in general metrizable spaces.
Differences Between Metrizable and Locally Compact Spaces
Metrizable spaces are topological spaces that can be endowed with a metric inducing their topology, enabling the use of distance-based concepts such as convergence and continuity. Locally compact spaces possess a neighborhood base consisting of compact sets, emphasizing compactness properties rather than a metric structure. The main difference lies in metrizability focusing on the existence of a metric defining the topology, while local compactness centers on the presence of compact neighborhoods, and these properties do not imply each other in general.
Relationships and Intersections: When Spaces Overlap
Metrizable spaces are topological spaces that can be endowed with a metric inducing their topology, while locally compact spaces have each point possessing a compact neighborhood, often facilitating analysis and measure theory. Spaces that are both metrizable and locally compact exhibit advantageous properties such as the existence of a compatible metric that respects the local compactness, enabling the application of powerful tools like the Riesz representation theorem. The intersection of these properties is prevalent in many spaces encountered in analysis, including Euclidean spaces and manifolds, where local compactness aligns with metrizability to provide a rich structural framework for convergence, continuity, and compactification techniques.
Examples of Metrizable Spaces
Metrizable spaces include classic examples like Euclidean spaces \(\mathbb{R}^n\) with the standard metric, ensuring properties such as completeness and separability. Other examples are discrete spaces, where the metric assigns distances of 0 or 1, and the Sorgenfrey line, which is metrizable but exhibits unique topological features. Understanding these examples highlights the distinction between metrizable spaces and locally compact spaces, where local compactness requires every point to have a compact neighborhood, a condition not guaranteed by metrizability alone.
Examples of Locally Compact Spaces
Locally compact spaces include important examples such as Euclidean spaces \(\mathbb{R}^n\), where every point has a compact neighborhood, and discrete spaces where every singleton set is compact. Many metrizable spaces are locally compact, but not all, such as the Sorgenfrey line, which is metrizable yet fails local compactness. Understanding these examples helps characterize the nuances between metrizable and locally compact spaces in topology.
Applications and Significance in Topology
Metrizable spaces, characterized by the existence of a metric inducing the topology, are crucial for applying analytic techniques and ensuring properties like paracompactness and separability in topology. Locally compact spaces, where every point has a compact neighborhood, play a significant role in harmonic analysis, measure theory, and the study of group actions on topological spaces. The interplay between metrizable and locally compact spaces facilitates the construction of one-point compactifications and supports foundational results in manifold theory and functional analysis.
Metrizable space Infographic
 libterm.com
libterm.com