Borel sets form the foundation of measure theory by encompassing all sets generated from open intervals through countable unions, intersections, and complements. Understanding Borel sets is essential for grasping key concepts in topology, probability, and real analysis. Dive deeper into the article to explore how these sets shape mathematical frameworks and your comprehension of measurable spaces.
Table of Comparison
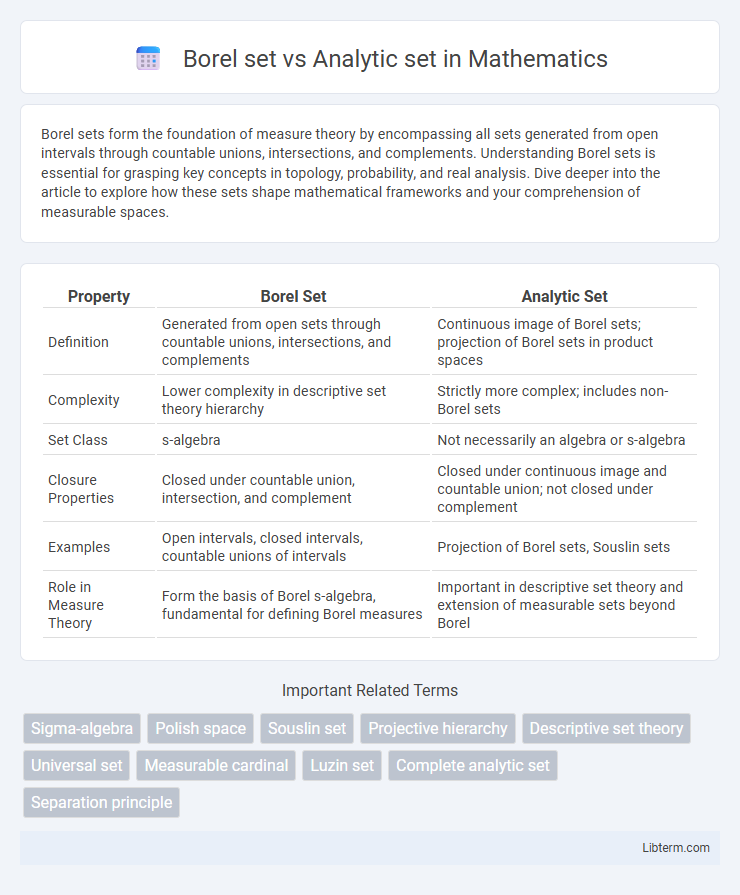
| Property | Borel Set | Analytic Set |
|---|---|---|
| Definition | Generated from open sets through countable unions, intersections, and complements | Continuous image of Borel sets; projection of Borel sets in product spaces |
| Complexity | Lower complexity in descriptive set theory hierarchy | Strictly more complex; includes non-Borel sets |
| Set Class | s-algebra | Not necessarily an algebra or s-algebra |
| Closure Properties | Closed under countable union, intersection, and complement | Closed under continuous image and countable union; not closed under complement |
| Examples | Open intervals, closed intervals, countable unions of intervals | Projection of Borel sets, Souslin sets |
| Role in Measure Theory | Form the basis of Borel s-algebra, fundamental for defining Borel measures | Important in descriptive set theory and extension of measurable sets beyond Borel |
Introduction to Borel and Analytic Sets
Borel sets are defined as the smallest s-algebra generated by open sets in a topological space, serving as the foundation for measurable spaces in real analysis and probability theory. Analytic sets, also known as Suslin sets, extend Borel sets by including continuous images of Borel sets, exhibiting more complex structures and capturing a broader class of sets not necessarily Borel. Understanding the distinction between Borel and analytic sets is crucial in descriptive set theory, particularly for the classification of sets in Polish spaces and the study of measurable and non-measurable phenomena.
Defining Borel Sets: Formal Foundations
Borel sets are generated from open sets through countable unions, intersections, and complements within a given topological space, forming the smallest s-algebra containing all open sets. Defined formally, the Borel s-algebra arises from transfinite iterations indexed by countable ordinals, creating a hierarchy of complexity known as the Borel hierarchy. This foundation underpins measurable functions and probability theory, distinguishing Borel sets from analytic sets, which are projections of Borel sets in product spaces and can exhibit higher descriptive complexity.
Analytic Sets: Concept and Characterization
Analytic sets, also known as Suslin sets, are a class of definable sets arising in descriptive set theory that strictly generalize Borel sets within Polish spaces. These sets can be characterized as continuous images of Borel sets or projections of Borel subsets from a product space, making them closed under continuous mappings and countable unions. Analytic sets play a crucial role in measure theory and effective descriptive set theory due to their definability and structural properties, despite not always being Borel measurable.
Hierarchical Structure: Borel vs. Analytic Sets
Borel sets form the smallest s-algebra generated by open sets, creating a well-defined hierarchical structure based on countable operations such as unions, intersections, and complements. Analytic sets, also called S11 sets, extend beyond Borel sets and include projections of Borel sets, placing them strictly higher in the projective hierarchy but still retaining strong descriptive set-theoretic properties. This hierarchical distinction reflects that every Borel set is analytic, while not all analytic sets are Borel, highlighting a fundamental separation in complexity and definability within descriptive set theory.
Examples of Borel Sets in Practice
Borel sets include all open and closed intervals in the real numbers, such as [0,1], (2,3), and their countable unions and intersections, making them foundational in probability theory and real analysis. For instance, intervals used to define measurable events in a probability space are Borel sets, and unions of countably many such intervals represent increasingly complex events. Analytic sets extend beyond Borel sets, often constructed as continuous images of Borel sets, encompassing more intricate structures that arise in descriptive set theory.
Examples and Properties of Analytic Sets
Analytic sets, also known as Suslin sets, extend beyond Borel sets by including continuous images of Borel sets, showcasing more complex structures not always captured by Borel hierarchies. For example, while every Borel set is analytic, there exist analytic sets that are not Borel, such as certain projection sets derived from Borel subsets of product spaces. Key properties of analytic sets include closure under continuous images and countable unions, and their characterization as projections of Borel sets from higher-dimensional spaces, highlighting their significance in descriptive set theory and measurable dynamics.
Key Differences: Borel Sets vs. Analytic Sets
Borel sets are generated from open sets through countable unions, intersections, and complements within a given topological space, forming the smallest s-algebra containing all open sets. Analytic sets, also known as Suslin sets, extend beyond Borel sets and are defined as continuous images of Borel sets from Polish spaces, often exhibiting more complex structures that cannot be captured by Borel operations alone. While every Borel set is analytic, there exist analytic sets that are not Borel, highlighting a strict inclusion and a nuanced hierarchy in descriptive set theory.
Relationships and Interconnections
Borel sets are the smallest s-algebra containing all open sets in a given topological space, serving as the foundation for measure theory and descriptive set theory. Analytic sets, also known as Suslin sets, are projections of Borel sets in a product space, making them strictly broader and encompassing complex structures not necessarily Borel. The relationship between Borel and analytic sets is crucial in understanding the hierarchy of definable sets, where every Borel set is analytic, but the converse fails, highlighting distinct levels of measurability and definability in mathematical analysis.
Applications in Descriptive Set Theory
Borel sets, generated from open sets through countable unions and intersections, serve as the foundational class of measurable sets in Descriptive Set Theory, crucial for analyzing definability and complexity in Polish spaces. Analytic sets, which are continuous images of Borel sets, extend beyond Borel hierarchy and enable handling of more complex sets that are not necessarily Borel, playing a key role in classification problems and projective hierarchy studies. Applications in Descriptive Set Theory leverage the properties of Borel sets for effective measurability and the broader descriptive power of analytic sets to address issues in determinacy, classification of equivalence relations, and definability of sets in Polish spaces.
Conclusion: Significance in Modern Mathematics
Borel sets form the foundation of descriptive set theory, representing the simplest definable sets in standard topologies through countable operations on open sets. Analytic sets, more complex and obtained as continuous images of Borel sets, capture a wider range of measurable phenomena essential in fields like functional analysis and probability theory. The distinction highlights the depth of set classification, impacting the study of definability, measurability, and the structure of mathematical objects in modern analysis and logic.
Borel set Infographic
 libterm.com
libterm.com