A contact manifold is a special type of odd-dimensional manifold equipped with a contact structure, which is a fully non-integrable hyperplane distribution. This structure plays a crucial role in differential geometry and dynamical systems by providing a geometric framework that generalizes the phase space in classical mechanics. Explore the rest of the article to discover how contact manifolds influence mathematical physics and topology, and why they matter in your studies or research.
Table of Comparison
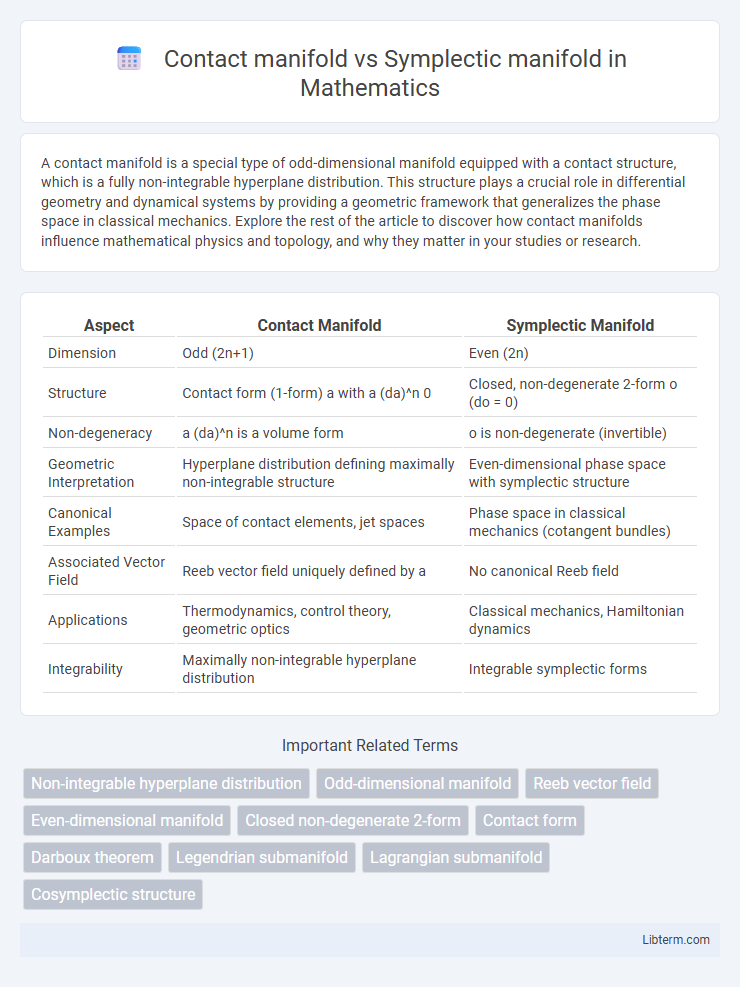
| Aspect | Contact Manifold | Symplectic Manifold |
|---|---|---|
| Dimension | Odd (2n+1) | Even (2n) |
| Structure | Contact form (1-form) a with a (da)^n 0 | Closed, non-degenerate 2-form o (do = 0) |
| Non-degeneracy | a (da)^n is a volume form | o is non-degenerate (invertible) |
| Geometric Interpretation | Hyperplane distribution defining maximally non-integrable structure | Even-dimensional phase space with symplectic structure |
| Canonical Examples | Space of contact elements, jet spaces | Phase space in classical mechanics (cotangent bundles) |
| Associated Vector Field | Reeb vector field uniquely defined by a | No canonical Reeb field |
| Applications | Thermodynamics, control theory, geometric optics | Classical mechanics, Hamiltonian dynamics |
| Integrability | Maximally non-integrable hyperplane distribution | Integrable symplectic forms |
Introduction to Contact and Symplectic Manifolds
Contact manifolds are odd-dimensional spaces equipped with a maximally non-integrable hyperplane distribution defined by a contact form, creating a geometric structure that generalizes phase spaces with constraints. Symplectic manifolds, in contrast, are even-dimensional smooth manifolds endowed with a closed, nondegenerate 2-form called the symplectic form, serving as the foundational framework of Hamiltonian mechanics. The study of contact and symplectic manifolds reveals deep relationships between geometry, topology, and physics, particularly in the formalism of classical and quantum mechanics.
Fundamental Definitions and Concepts
A contact manifold is an odd-dimensional smooth manifold equipped with a contact structure, defined by a maximally non-integrable hyperplane distribution given locally by the kernel of a contact 1-form, a, satisfying a (da)n 0 for 2n+1 dimensions. In contrast, a symplectic manifold is an even-dimensional smooth manifold endowed with a closed, non-degenerate 2-form o, meaning do = 0 and on provides a volume form on the manifold. The fundamental difference lies in the contact manifold's hyperplane field encoding a geometric structure that is locally maximally non-integrable, while the symplectic manifold carries a globally defined, closed, non-degenerate form essential for Hamiltonian mechanics.
Geometric Structures: Comparing Contact and Symplectic Manifolds
Contact manifolds are odd-dimensional geometric structures equipped with a maximally non-integrable hyperplane distribution defined by a contact form, whereas symplectic manifolds are even-dimensional and carry a closed, non-degenerate 2-form called the symplectic form. The contact structure defines a unique Reeb vector field, essential in studying dynamics and geometric flows, while symplectic geometry underpins Hamiltonian mechanics through the symplectic form's role in preserving volume and defining Poisson brackets. Both structures encode rich geometric and dynamical information but differ fundamentally in dimensionality and integrability conditions, which influence their applications in topology and mathematical physics.
Dimensional Differences: Odd vs Even Manifolds
Contact manifolds are characterized by their odd dimensions, specifically 2n+1, where n is a nonnegative integer, reflecting their role in geometric structures with a hyperplane distribution defined by a contact form. Symplectic manifolds, on the other hand, are even-dimensional, typically of dimension 2n, equipped with a closed non-degenerate 2-form that provides a framework for Hamiltonian dynamics and classical mechanics. The dimensional difference fundamentally distinguishes these manifolds: contact manifolds serve as odd-dimensional analogues related to the boundary behavior of symplectic manifolds, which themselves describe even-dimensional phase spaces.
Local vs Global Properties
Contact manifolds exhibit a codimension-one hyperplane distribution with a non-integrable condition, leading to local Darboux charts that resemble the standard contact structure, but their global topology can vary significantly due to phenomena like overtwistedness. Symplectic manifolds possess a closed, non-degenerate 2-form, ensuring local canonical forms via Darboux's theorem, while global properties involve intricate constraints such as symplectic capacities and rigidity. The contrast lies in contact manifolds' flexibility in global topology versus symplectic manifolds' stronger global invariants and restrictions despite similar local normal forms.
Canonical Examples in Mathematics and Physics
Contact manifolds, characterized by a maximally non-integrable hyperplane distribution, naturally appear in the phase space of thermodynamics and geometric optics, represented by the contact form on \(\mathbb{R}^{2n+1}\). Symplectic manifolds, equipped with a closed, non-degenerate 2-form, serve as the mathematical foundation for classical mechanics and Hamiltonian systems, with canonical examples including \((\mathbb{R}^{2n}, \omega = \sum dx_i \wedge dp_i)\) and cotangent bundles \(T^*Q\). The correspondence between these manifolds is seen through symplectization, linking contact structures to symplectic cones and bridging contact geometry's topological invariants with symplectic geometry's Hamiltonian dynamics.
Differential Forms: Contact vs Symplectic
Symplectic manifolds are characterized by a closed non-degenerate 2-form o, which provides a rich structure used in Hamiltonian mechanics and ensures even-dimensionality. Contact manifolds are defined by a contact form a, a 1-form whose maximal non-integrability condition a (da)^n 0 uniquely determines an odd-dimensional manifold structure. The distinction lies in the differential forms: symplectic geometry relies on a closed 2-form preserving volume, while contact geometry depends on a 1-form with its exterior derivative defining a hyperplane distribution without integrability.
Transformation Groups and Their Actions
Transformation groups acting on contact manifolds preserve the contact structure defined by a maximally non-integrable hyperplane distribution, inducing contactomorphisms that maintain the contact form up to a conformal factor. In contrast, symplectic manifolds admit symplectomorphisms arising from transformation groups preserving a closed non-degenerate 2-form, ensuring volume and orientation conservation. The interplay between these transformation groups highlights fundamental differences in geometric rigidity: contact group actions reflect flexibility through conformal rescalings, whereas symplectic actions enforce strict invariance of the symplectic form, influencing dynamical properties and classification results.
Applications in Geometry and Topology
Contact manifolds, characterized by a maximally non-integrable hyperplane distribution, are pivotal in studying odd-dimensional geometric structures, especially in fields like CR geometry and the topology of 3-manifolds. Symplectic manifolds, equipped with a closed, non-degenerate 2-form, serve as the foundational setting for Hamiltonian dynamics and play a crucial role in the study of smooth even-dimensional topology, including Floer homology and mirror symmetry. Applications in geometry and topology leverage contact structures to analyze fillability and tightness conditions, while symplectic manifolds facilitate the understanding of invariants such as Gromov-Witten and symplectic capacities.
Summary: Key Distinctions and Relationships
Contact manifolds are odd-dimensional spaces equipped with a maximally non-integrable hyperplane distribution defined by a contact form, while symplectic manifolds are even-dimensional and possess a closed, non-degenerate 2-form called the symplectic form. The key distinction lies in their dimensionality and structural properties: contact manifolds model the geometric framework for phase spaces with constraints, whereas symplectic manifolds provide the foundation for classical Hamiltonian mechanics without constraints. These structures are related through symplectization, where a contact manifold can be embedded into a symplectic manifold, reflecting the intimate link between constrained and unconstrained dynamical systems.
Contact manifold Infographic
 libterm.com
libterm.com