The cross product is a fundamental operation in vector mathematics, resulting in a vector perpendicular to the plane formed by two input vectors. This operation is widely used in physics, engineering, and computer graphics to determine torque, rotational forces, and normal vectors. Explore the rest of the article to uncover the detailed applications and calculation methods of the cross product.
Table of Comparison
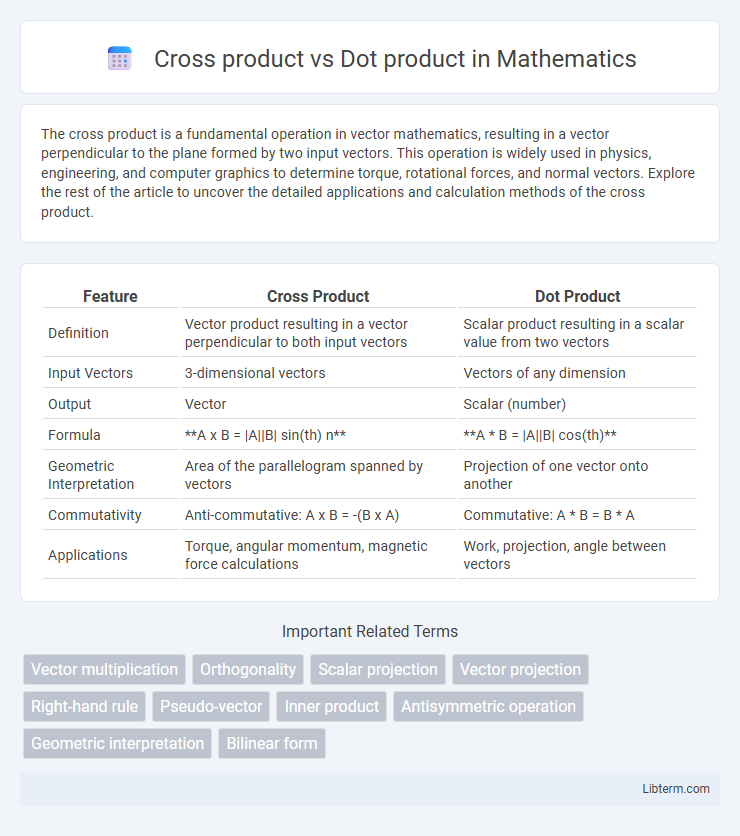
| Feature | Cross Product | Dot Product |
|---|---|---|
| Definition | Vector product resulting in a vector perpendicular to both input vectors | Scalar product resulting in a scalar value from two vectors |
| Input Vectors | 3-dimensional vectors | Vectors of any dimension |
| Output | Vector | Scalar (number) |
| Formula | A x B = |A||B| sin(th) n | A * B = |A||B| cos(th) |
| Geometric Interpretation | Area of the parallelogram spanned by vectors | Projection of one vector onto another |
| Commutativity | Anti-commutative: A x B = -(B x A) | Commutative: A * B = B * A |
| Applications | Torque, angular momentum, magnetic force calculations | Work, projection, angle between vectors |
Introduction to Cross Product and Dot Product
The cross product is a vector operation that produces a vector perpendicular to the plane formed by two input vectors, commonly used in physics and engineering to calculate torque and rotational force. The dot product, also known as the scalar product, yields a scalar value representing the magnitude of projection of one vector onto another, essential in measuring angles and work done. Both products are fundamental in vector algebra but serve different geometric and physical interpretations, with the cross product emphasizing direction and the dot product emphasizing magnitude correlation.
Definitions and Mathematical Formulations
The cross product is a vector operation defined for two three-dimensional vectors, resulting in a vector perpendicular to both original vectors, mathematically expressed as A x B = |A||B| sin(th) n, where th is the angle between vectors A and B, and n is the unit vector orthogonal to the plane containing A and B. The dot product, on the other hand, is a scalar operation defined as A * B = |A||B| cos(th), representing the magnitude of one vector projected onto another. Both products are foundational in vector calculus and physics, with the cross product used to find torque or rotational effects and the dot product used to measure work or projection.
Geometric Interpretation
The cross product of two vectors results in a vector perpendicular to the plane containing the original vectors, with magnitude equal to the area of the parallelogram they span, emphasizing direction and orientation in three-dimensional space. In contrast, the dot product produces a scalar representing the projection of one vector onto another, quantifying their directional alignment through the cosine of the angle between them. Geometrically, the dot product measures similarity in direction, while the cross product captures the spatial relationship and magnitude of the vectors' orthogonal interaction.
Key Differences Between Cross Product and Dot Product
The cross product produces a vector perpendicular to two given vectors, representing their area and orientation in 3D space, while the dot product yields a scalar indicating the cosine of the angle between the vectors, reflecting their directional similarity. Cross product magnitude equals the product of the vectors' magnitudes and the sine of the angle between them, whereas the dot product equals the product of the magnitudes and the cosine of the angle. The cross product is applicable only in three-dimensional space, contrasting with the dot product's use across any dimensional vector spaces.
Applications in Physics and Engineering
The cross product is essential in physics and engineering for calculating torque, angular momentum, and magnetic force, where vector direction and magnitude perpendicular to two vectors are crucial. The dot product is widely used to determine work done by a force, projection of vectors, and in signal processing for measuring similarity between signals. Both products enable precise analysis of vector relationships critical to mechanical systems, electromagnetism, and structural engineering.
Properties and Rules
The cross product produces a vector perpendicular to the two input vectors with magnitude equal to the area of the parallelogram they span, following the right-hand rule, and is anti-commutative (A x B = -B x A). The dot product results in a scalar equal to the product of the magnitudes of the two vectors and the cosine of the angle between them, exhibiting commutativity (A * B = B * A) and distributivity over vector addition. Both operations satisfy linearity, but the cross product is only defined in three-dimensional space, while the dot product applies in any dimension.
Calculation Examples
The cross product of vectors A = (2, 3, 4) and B = (5, 6, 7) is calculated as A x B = (3*7 - 4*6, 4*5 - 2*7, 2*6 - 3*5) = (-3, 6, -3), yielding a vector orthogonal to both A and B. The dot product of the same vectors is A * B = 2*5 + 3*6 + 4*7 = 56, resulting in a scalar representing the magnitude projection of one vector onto another. These operations highlight the differences: the cross product produces a vector related to area and direction, while the dot product produces a scalar related to magnitude and angle.
Cross Product in 3D Space
The cross product in 3D space is a vector operation that produces a vector perpendicular to the plane formed by two input vectors, with a magnitude equal to the area of the parallelogram they span. This operation is fundamental in physics and engineering for computing torque, angular momentum, and determining the normal vector to surfaces. Unlike the dot product, which results in a scalar representing the magnitude of projection, the cross product yields a vector with both direction and magnitude critical for spatial analyses.
Dot Product in Vector Projection
The dot product calculates the scalar projection of one vector onto another, essential for determining vector projections in physics and engineering. By multiplying the magnitudes of two vectors and the cosine of the angle between them, the dot product quantifies how much one vector extends in the direction of another. This property makes the dot product fundamental for vector projection, contrasting with the cross product that produces a vector orthogonal to the initial vectors.
Choosing the Right Product for Your Problem
Choosing between the cross product and dot product depends on the nature of your problem and the desired outcome. Use the dot product when you need to determine the angle between two vectors or project one vector onto another, as it provides a scalar representing similarity or alignment. Opt for the cross product when you require a vector perpendicular to two given vectors, useful in calculating torque, rotational forces, or finding normal vectors to surfaces.
Cross product Infographic
 libterm.com
libterm.com