Cobordism spectrum plays a crucial role in algebraic topology by providing a framework for classifying manifolds through cobordism classes, linking geometric and homotopical properties. This tool helps in understanding complex relationships between manifolds and stable homotopy theory, thereby offering deep insights into topological invariants. Explore the rest of the article to uncover how cobordism spectrum shapes modern mathematical research and your grasp of topology.
Table of Comparison
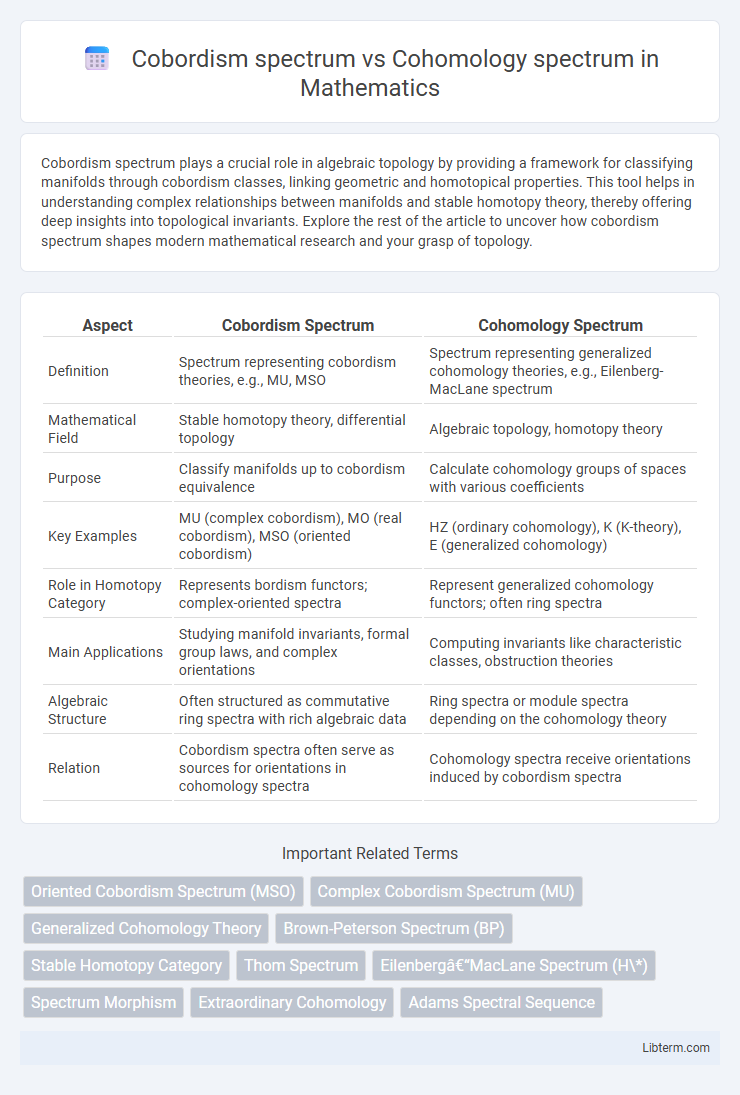
| Aspect | Cobordism Spectrum | Cohomology Spectrum |
|---|---|---|
| Definition | Spectrum representing cobordism theories, e.g., MU, MSO | Spectrum representing generalized cohomology theories, e.g., Eilenberg-MacLane spectrum |
| Mathematical Field | Stable homotopy theory, differential topology | Algebraic topology, homotopy theory |
| Purpose | Classify manifolds up to cobordism equivalence | Calculate cohomology groups of spaces with various coefficients |
| Key Examples | MU (complex cobordism), MO (real cobordism), MSO (oriented cobordism) | HZ (ordinary cohomology), K (K-theory), E (generalized cohomology) |
| Role in Homotopy Category | Represents bordism functors; complex-oriented spectra | Represent generalized cohomology functors; often ring spectra |
| Main Applications | Studying manifold invariants, formal group laws, and complex orientations | Computing invariants like characteristic classes, obstruction theories |
| Algebraic Structure | Often structured as commutative ring spectra with rich algebraic data | Ring spectra or module spectra depending on the cohomology theory |
| Relation | Cobordism spectra often serve as sources for orientations in cohomology spectra | Cohomology spectra receive orientations induced by cobordism spectra |
Introduction to Cobordism and Cohomology Spectra
Cobordism spectrum serves as a foundational tool in algebraic topology, representing structured manifolds up to cobordism equivalence and enabling the classification of manifold invariants via homotopy-theoretic methods. Cohomology spectra generalize cohomology theories by encoding cohomological information into spectra, facilitating stable homotopy-theoretic computations and connecting classical cohomology with generalized cohomology theories. Together, these spectra bridge geometric topology and homotopy theory, allowing for deep insights into manifold structures and cohomological properties through a unifying spectral framework.
Foundational Concepts: Spectra in Stable Homotopy Theory
In stable homotopy theory, the Cobordism spectrum captures geometric information about manifolds up to cobordism, serving as a fundamental object encoding bordism classes and characteristic classes. The Cohomology spectrum, on the other hand, generalizes classical cohomology theories by representing cohomology groups as homotopy classes of maps into a spectrum, enabling powerful computational and structural tools. Both spectra arise as foundational constructs, where the former reflects manifold-based equivalence relations and the latter encodes algebraic invariants via stable homotopy classes.
Defining Cobordism Spectrum: Origins and Structure
The Cobordism spectrum originates from the study of manifolds and their equivalence under cobordism, providing a foundational object in stable homotopy theory that encodes geometric information about manifold classes. Its structure is defined through the Thom spectra associated with vector bundles, capturing genera and characteristic classes via homotopical methods. This spectrum serves as a bridge between differential topology and algebraic topology, enabling the computation of cobordism rings and linking geometric invariants with cohomological operations.
Understanding Cohomology Spectrum: Types and Examples
Cohomology spectra generalize cohomology theories by representing them as structured sequences of spaces or spectra that encode algebraic invariants topologically. Prominent examples include the Eilenberg-MacLane spectrum, which realizes ordinary cohomology with abelian group coefficients, and complex K-theory spectrum representing topological K-theory. Understanding various types of cohomology spectra involves studying their homotopy groups and ring structures, crucial for applications in stable homotopy theory and the classification of topological spaces.
Comparing Cobordism and Cohomology Spectra
Cobordism spectra represent generalized homology theories that classify manifolds up to cobordism, encoding geometric information through stable homotopy types, while cohomology spectra correspond to generalized cohomology theories capturing algebraic invariants of spaces. The complex cobordism spectrum MU provides a universal example closely linked to formal group laws, unlike ordinary cohomology spectra such as singular cohomology represented by the Eilenberg-MacLane spectrum HZ. Comparing these spectra reveals deep connections between geometric topology and algebraic structures, with cobordism spectra often enabling computations in stable homotopy theory that cohomology spectra alone cannot achieve.
Algebraic and Geometric Interpretations
Cobordism spectra represent classes of manifolds under boundary relations, encoding geometric information about manifold structures and embeddings, while cohomology spectra arise from generalized cohomology theories capturing algebraic invariants of topological spaces through stable homotopy types. Algebraically, the cobordism spectrum corresponds to complex-oriented ring spectra linked to formal group laws, facilitating computations in stable homotopy theory, whereas cohomology spectra define multiplicative cohomology operations reflecting the algebraic structure of cochains. Geometrically, cobordism spectra classify manifolds up to cobordism equivalence, connecting geometry with homotopy-theoretic invariants, and cohomology spectra interpret properties of spaces via sheaf cohomology and characteristic classes.
Key Theorems Connecting Cobordism and Cohomology
The Pontryagin-Thom theorem establishes a fundamental equivalence between cobordism classes and homotopy classes of maps into Thom spectra, linking cobordism theories with stable homotopy theory. The Atiyah-Hirzebruch spectral sequence facilitates the computation of cobordism groups by relating them to singular cohomology with coefficients in complex cobordism or oriented cobordism spectra. Quillen's theorem identifies complex cobordism as a universal complex-oriented cohomology theory, connecting the formal group laws in complex cobordism spectra to the structure of cohomology theories.
Applications in Topology and Homotopy Theory
Cobordism spectra, such as MU and MO, play a central role in classifying manifolds up to cobordism and detecting geometric structures in stable homotopy theory, providing a foundation for understanding manifold invariants and formal group laws. Cohomology spectra, including Eilenberg-MacLane spectra and complex K-theory spectra, serve as algebraic tools for generalized cohomology theories, enabling computations of homotopy groups and the analysis of spectral sequences in stable homotopy categories. Applications in topology and homotopy theory leverage the interplay between cobordism and cohomology spectra to study vector bundles, characteristic classes, and the structure of stable homotopy groups of spheres with profound implications for classification problems and dualities.
Computational Methods and Invariants
Cobordism spectra provide a structured approach to compute stable homotopy groups by encoding geometric relationships between manifolds, while cohomology spectra facilitate algebraic computations through generalized cohomology theories. Computational methods for cobordism often rely on spectral sequences such as the Adams-Novikov spectral sequence to extract invariants like formal group laws and characteristic classes. Cohomology spectra enable efficient calculation of invariants including Steenrod operations and Ext groups, offering algebraic tools that complement the geometric intuition derived from cobordism theories.
Future Directions and Open Problems
Cobordism spectra, such as the Thom spectrum MU, play a fundamental role in stable homotopy theory and provide deep connections to complex-oriented cohomology theories. Future directions involve refining the computational techniques for stable homotopy groups derived from cobordism spectra and exploring their relationships with motivic homotopy theory and equivariant stable homotopy categories. Open problems include understanding the full structure of cooperations in generalized cohomology theories and developing explicit characterizations of the map between cobordism spectra and cohomology spectra that capture higher chromatic height phenomena.
Cobordism spectrum Infographic
 libterm.com
libterm.com