A graph visually represents data points connected by edges, making complex relationships easier to understand and analyze. Understanding how to interpret different types of graphs can significantly enhance your ability to draw insights from information. Explore the rest of the article to learn how to effectively use graphs in various contexts.
Table of Comparison
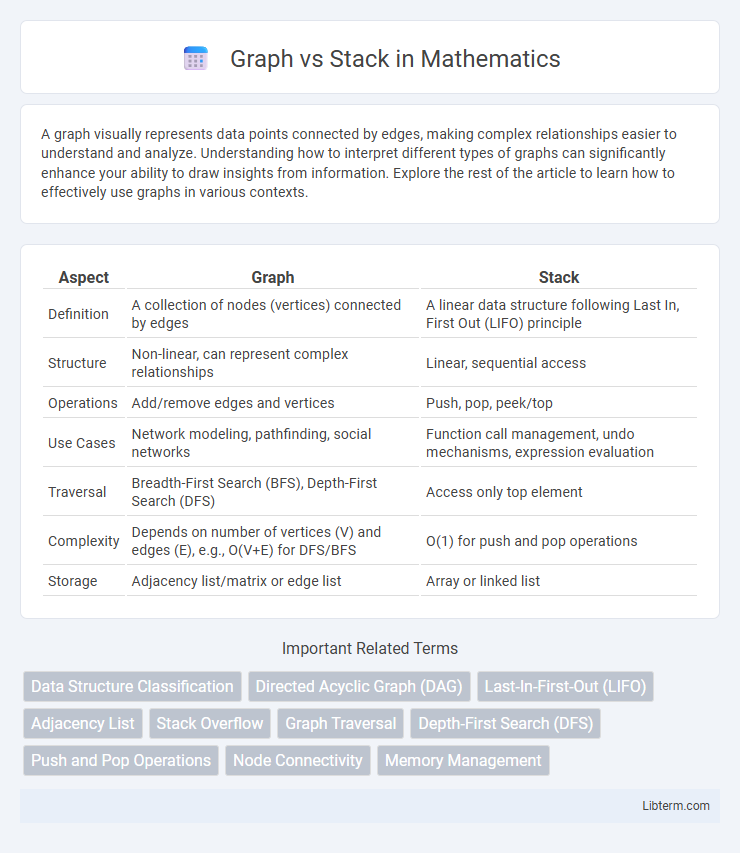
| Aspect | Graph | Stack |
|---|---|---|
| Definition | A collection of nodes (vertices) connected by edges | A linear data structure following Last In, First Out (LIFO) principle |
| Structure | Non-linear, can represent complex relationships | Linear, sequential access |
| Operations | Add/remove edges and vertices | Push, pop, peek/top |
| Use Cases | Network modeling, pathfinding, social networks | Function call management, undo mechanisms, expression evaluation |
| Traversal | Breadth-First Search (BFS), Depth-First Search (DFS) | Access only top element |
| Complexity | Depends on number of vertices (V) and edges (E), e.g., O(V+E) for DFS/BFS | O(1) for push and pop operations |
| Storage | Adjacency list/matrix or edge list | Array or linked list |
Introduction to Graphs and Stacks
Graphs represent complex relationships through nodes (vertices) connected by edges, enabling modeling of networks, social connections, and dependencies. Stacks operate as linear data structures following Last-In-First-Out (LIFO) principle, allowing controlled access to elements via push and pop operations. Understanding graph traversal algorithms contrasts with stack-based operations like recursion management, highlighting distinct applications in computer science.
Core Concepts: Defining Graphs
Graphs are mathematical structures consisting of vertices (nodes) connected by edges, representing relationships between entities, and can be either directed or undirected. Core concepts include understanding adjacency, where edges define connections between pairs of nodes, and distinguishing between weighted and unweighted graphs based on whether edges carry values. Unlike stacks that operate on a Last In, First Out (LIFO) principle for data management, graphs model complex networks without a linear order.
Core Concepts: Understanding Stacks
Stacks are linear data structures that follow the Last In, First Out (LIFO) principle, where elements are added (pushed) and removed (popped) from the top. They support core operations such as push, pop, peek (top element), and isEmpty, enabling efficient management of data in scenarios like function call management and expression evaluation. Unlike graphs, which represent complex relationships as nodes and edges, stacks emphasize sequential data processing with constant time complexity for primary operations.
Key Differences Between Graphs and Stacks
Graphs represent complex structures with nodes (vertices) connected by edges, enabling modeling of relationships and networks, while stacks are linear data structures organized by the Last-In-First-Out (LIFO) principle for managing order-sensitive operations. Graphs support various traversal algorithms like Depth-First Search and Breadth-First Search to explore connections, whereas stacks facilitate function call management and expression evaluation through push and pop operations. The core distinction lies in graphs' ability to represent non-linear connections versus stacks' strict sequential element access.
Data Structure Applications: Graphs vs Stacks
Graphs excel in modeling complex relationships and networks such as social connections, web page linking, and transportation systems, enabling efficient pathfinding and connectivity analysis. Stacks provide a straightforward, Last-In-First-Out (LIFO) structure ideal for function call management, expression evaluation, and backtracking algorithms. Choosing between graphs and stacks depends on whether the application requires intricate relationship representation or simple, reversible processing sequences.
Memory Usage in Graphs and Stacks
Graphs typically require more memory than stacks due to storing nodes and edges, with adjacency matrices consuming O(V^2) space and adjacency lists using O(V + E), where V is vertices and E is edges. Stacks use linear memory proportional to the number of elements, O(n), since they only store values in a simple LIFO structure without extra pointers or references. Memory efficiency in graphs depends on representation choice, while stacks maintain minimal overhead, making them more memory-friendly for sequential data processing.
Performance Analysis: Graphs vs Stacks
Graphs and stacks differ significantly in performance depending on their application and operations performed. Graphs, with complex relationships and adjacency lists or matrices, often require more time for traversal algorithms like BFS or DFS, resulting in O(V+E) time complexity, where V is vertices and E is edges. Stacks, implemented as arrays or linked lists, provide faster, constant-time O(1) push and pop operations, excelling in scenarios requiring last-in-first-out (LIFO) data management and simpler linear data traversal.
Common Algorithms for Graphs and Stacks
Graphs commonly utilize algorithms such as Depth-First Search (DFS), Breadth-First Search (BFS), Dijkstra's shortest path, and Kruskal's minimum spanning tree, which efficiently explore nodes and edges to solve complex network problems. Stacks predominantly employ algorithms for expression evaluation, depth tracking in DFS, backtracking, and undo mechanisms due to their Last-In-First-Out (LIFO) structure. Both structures are foundational in computer science, with graph algorithms focusing on node relationships and traversal, while stack algorithms emphasize order management and recursive process handling.
Real-World Use Cases: Graphs and Stacks
Graphs excel in modeling complex relationships such as social networks, recommendation systems, and transportation routes, where nodes represent entities and edges depict connections or flows. Stacks are ideal for managing function calls, undo mechanisms, and expression evaluations in programming, leveraging their LIFO (Last In, First Out) structure for efficient data handling. Real-world applications rely on graphs for network analysis and pathfinding algorithms, while stacks underpin algorithm design and system runtime processes.
Choosing the Right Data Structure: Graph or Stack
Choosing the right data structure depends on the problem's nature: use a graph for representing complex relationships, networks, or paths with nodes and edges, enabling traversal algorithms like BFS or DFS. Opt for a stack when managing linear, last-in-first-out (LIFO) operations such as expression evaluation, backtracking, or function call management. Understanding the task's structural requirements and access patterns is crucial to selecting between a graph and a stack for optimal performance and clarity.
Graph Infographic
 libterm.com
libterm.com