Isomorphism describes a structure-preserving relationship between two mathematical objects, where one can be transformed into the other without losing essential properties. This concept applies across various fields, including algebra, graph theory, and computer science, helping to identify equivalences and symmetries. Explore the rest of the article to deepen your understanding of isomorphism and its practical applications.
Table of Comparison
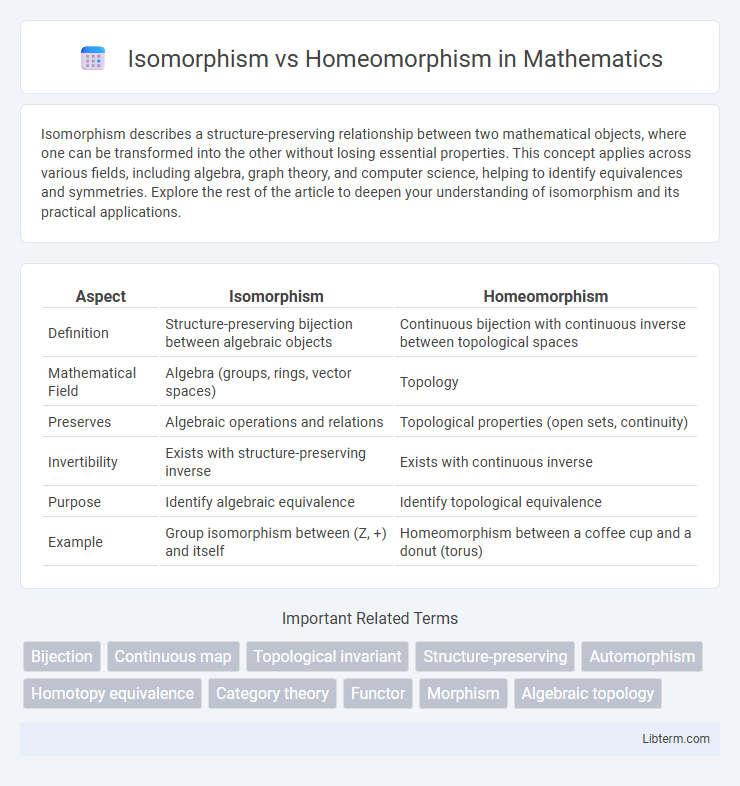
| Aspect | Isomorphism | Homeomorphism |
|---|---|---|
| Definition | Structure-preserving bijection between algebraic objects | Continuous bijection with continuous inverse between topological spaces |
| Mathematical Field | Algebra (groups, rings, vector spaces) | Topology |
| Preserves | Algebraic operations and relations | Topological properties (open sets, continuity) |
| Invertibility | Exists with structure-preserving inverse | Exists with continuous inverse |
| Purpose | Identify algebraic equivalence | Identify topological equivalence |
| Example | Group isomorphism between (Z, +) and itself | Homeomorphism between a coffee cup and a donut (torus) |
Introduction to Isomorphism and Homeomorphism
Isomorphism and homeomorphism are fundamental concepts in mathematics that describe structure-preserving mappings between objects. Isomorphism typically arises in algebra to denote a bijective map between algebraic structures, such as groups or rings, preserving operations and relations. Homeomorphism appears in topology, referring to a continuous, bijective function with a continuous inverse between topological spaces, indicating that the spaces are topologically equivalent.
Defining Isomorphism in Mathematics
Isomorphism in mathematics is a bijective mapping between two algebraic structures that preserves the operations and relations defining those structures, ensuring they are structurally identical. Unlike homeomorphisms, which relate topological spaces via continuous functions with continuous inverses, isomorphisms apply broadly to groups, rings, vector spaces, and other algebraic systems. This structural preservation allows mathematicians to classify objects up to isomorphism, recognizing them as essentially the same in abstract algebra.
Understanding Homeomorphism in Topology
Homeomorphism in topology refers to a continuous, bijective function between two topological spaces with a continuous inverse, indicating that the spaces are topologically equivalent. This concept preserves properties such as connectedness and compactness, allowing for the classification of spaces by their intrinsic shape rather than their geometric form. Unlike isomorphism in algebra, which concerns structure-preserving maps between algebraic objects, homeomorphism centers on the deformation of spaces without tearing or gluing.
Key Differences Between Isomorphism and Homeomorphism
Isomorphism refers to a structure-preserving bijection between algebraic objects such as groups, rings, or graphs, ensuring that operations and relations are maintained exactly. Homeomorphism is a continuous bijection with a continuous inverse between topological spaces, preserving topological properties like connectedness and compactness rather than algebraic structure. The key difference lies in isomorphisms preserving algebraic operations and homeomorphisms focusing on topological equivalence.
Core Properties of Isomorphic Structures
Isomorphism focuses on the preservation of algebraic structures such as groups, rings, or vector spaces, ensuring a bijective map that respects operations like addition and multiplication. Core properties of isomorphic structures include the exact preservation of identity elements, inverses, and the operation results, indicating structural equivalence rather than mere similarity. Unlike homeomorphisms, which emphasize topological properties such as continuity and open sets, isomorphisms maintain the algebraic integrity and operational framework within mathematical objects.
Essential Characteristics of Homeomorphic Spaces
Homeomorphic spaces are characterized by a continuous, bijective mapping with a continuous inverse, preserving topological properties such as connectedness, compactness, and the number of holes. Unlike isomorphisms in algebra that preserve structure like operations and relations, homeomorphisms focus on the shape and spatial properties without distortion or tearing. Essential traits of homeomorphic spaces include topological equivalence and invariance under continuous deformations, ensuring that properties like genus and boundary features remain unchanged.
Examples Illustrating Isomorphism
Isomorphism in mathematics exemplifies structural equivalence between algebraic objects, such as groups, rings, or vector spaces, where a bijective map preserves operations. For instance, the group of integers modulo n under addition, \(\mathbb{Z}/n\mathbb{Z}\), is isomorphic to the cyclic group of order n, \(\mathbb{Z}_n\), demonstrating isomorphic group structure despite different representations. Another example includes the vector space isomorphism between \(\mathbb{R}^n\) and the space of n-tuples of real numbers, illustrating that they share identical linear structure and dimension.
Real-World Applications of Homeomorphism
Homeomorphism plays a critical role in real-world applications by providing a framework to understand continuous deformations in topology, such as in material sciences where it models the malleability of objects without tearing or gluing. This concept is essential in computer graphics and animation for shape morphing and surface modeling, ensuring that transformations preserve topological properties. In robotics and medical imaging, homeomorphism aids in path planning and the reconstruction of anatomical structures by guaranteeing continuous and reversible mappings.
Choosing Between Isomorphism and Homeomorphism
Choosing between isomorphism and homeomorphism depends on the structures to be compared: isomorphism applies to algebraic structures such as groups, rings, or vector spaces by preserving operations, while homeomorphism pertains to topological spaces by preserving continuous deformation properties. When the goal is to analyze structural equivalence in algebra, isomorphism provides a precise correspondence between elements and operations, enabling algebraic manipulation and classification. For problems involving geometric or topological properties like connectivity or compactness, homeomorphism offers a framework to understand spaces up to continuous transformation without tearing or gluing.
Summary: Isomorphism vs Homeomorphism
Isomorphism and homeomorphism are both concepts that describe equivalence between mathematical structures, but they apply in different contexts: isomorphism relates to algebraic structures preserving operations, while homeomorphism pertains to topological spaces preserving continuity and open sets. An isomorphism demonstrates a bijective map maintaining algebraic operations like addition or multiplication, making two structures structurally identical in algebra. A homeomorphism is a continuous bijection with a continuous inverse, showing two topological spaces are topologically indistinguishable.
Isomorphism Infographic
 libterm.com
libterm.com