A continuous operator is a fundamental concept in functional analysis that ensures stability and predictability when mapping elements between normed vector spaces. It preserves limits, meaning small changes in input produce small changes in output, which is essential for solving differential equations and optimization problems. Discover how continuous operators function and their crucial applications in advanced mathematics throughout this article.
Table of Comparison
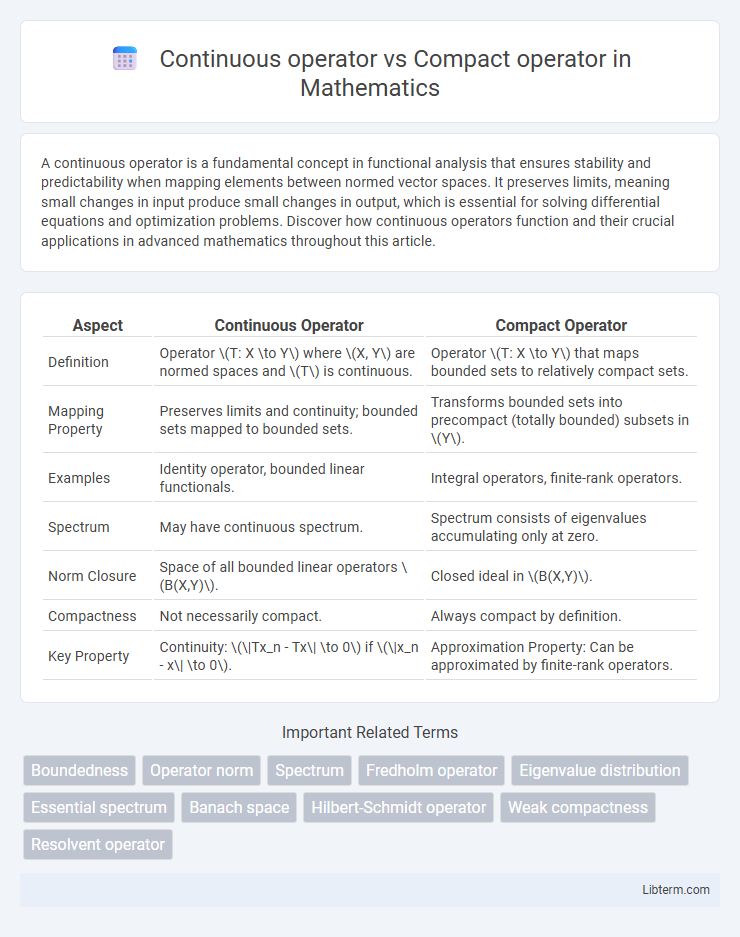
| Aspect | Continuous Operator | Compact Operator |
|---|---|---|
| Definition | Operator \(T: X \to Y\) where \(X, Y\) are normed spaces and \(T\) is continuous. | Operator \(T: X \to Y\) that maps bounded sets to relatively compact sets. |
| Mapping Property | Preserves limits and continuity; bounded sets mapped to bounded sets. | Transforms bounded sets into precompact (totally bounded) subsets in \(Y\). |
| Examples | Identity operator, bounded linear functionals. | Integral operators, finite-rank operators. |
| Spectrum | May have continuous spectrum. | Spectrum consists of eigenvalues accumulating only at zero. |
| Norm Closure | Space of all bounded linear operators \(B(X,Y)\). | Closed ideal in \(B(X,Y)\). |
| Compactness | Not necessarily compact. | Always compact by definition. |
| Key Property | Continuity: \(\|Tx_n - Tx\| \to 0\) if \(\|x_n - x\| \to 0\). | Approximation Property: Can be approximated by finite-rank operators. |
Introduction to Operators in Functional Analysis
Continuous operators in functional analysis are mappings between normed vector spaces that preserve limits, ensuring boundedness and stability of functional sequences. Compact operators form a subclass characterized by their ability to map bounded sets into relatively compact ones, leading to sequence images having convergent subsequences. Understanding the distinction between continuous and compact operators is fundamental for spectral theory and applications in solving integral and differential equations.
Defining Continuous Operators
Continuous operators in functional analysis are mappings between topological vector spaces that preserve the convergence of sequences, ensuring that the image of a convergent sequence converges to the image of the limit. These operators are defined by the property that for every open set in the codomain, the preimage under the operator is open in the domain, guaranteeing continuity in the topological sense. Understanding continuous operators is fundamental, as they form the broader class from which compact operators--those that map bounded sets to relatively compact sets--are a specialized subset.
Understanding Compact Operators
Compact operators on Banach or Hilbert spaces map bounded sets to relatively compact (precompact) sets, meaning their image has compact closure, which plays a crucial role in spectral theory and functional analysis. Unlike general continuous operators that only guarantee boundedness, compact operators often admit approximations by finite-rank operators, enabling powerful decomposition techniques such as the Riesz-Schauder theory. Understanding compact operators involves analyzing their ability to "compress" infinite-dimensional behavior into manageable finite-dimensional approximations, making them indispensable in solving integral equations and studying operator spectra.
Core Differences Between Continuous and Compact Operators
Continuous operators map bounded sets to bounded sets, preserving the structure of the space without necessarily compressing dimensions. Compact operators, a subset of continuous operators, map bounded sets to relatively compact sets, meaning their images have compact closure, often allowing approximation by finite-rank operators. The core difference lies in compact operators exhibiting stronger properties like having discrete spectra with possible accumulation only at zero, whereas general continuous operators do not guarantee such spectral characteristics.
Key Properties of Continuous Operators
Continuous operators on normed spaces preserve limits and ensure boundedness, meaning they map bounded sets to bounded sets. Key properties include linearity, continuity at every point, and the equivalence between continuity and boundedness for linear operators. Unlike compact operators, which map bounded sets to relatively compact sets, continuous operators may not reduce dimensionality or exhibit approximation properties.
Important Features of Compact Operators
Compact operators on Banach spaces transform bounded sets into relatively compact sets, ensuring sequences have convergent subsequences within their image. They can be approximated by finite-rank operators, which provides crucial insights into spectral theory, as their spectrum consists of at most countably many eigenvalues accumulating only at zero. Unlike general continuous operators, compact operators exhibit essential properties such as the Fredholm alternative and have a discrete spectrum outside zero, making them fundamental in functional analysis.
Examples Illustrating Each Operator Type
The identity operator on an infinite-dimensional Hilbert space provides a classic example of a continuous operator that is not compact, as it maps bounded sets to bounded sets but does not map the unit ball into a relatively compact set. In contrast, the Hilbert-Schmidt integral operators with square-integrable kernels serve as prototypical compact operators, transforming infinite-dimensional spaces while approximating finite-rank operators arbitrarily closely. Operators given by infinite diagonal matrices with entries tending to zero also exemplify compact operators, illustrating how spectral properties reflect compactness through eigenvalue decay.
Applications in Mathematical Analysis
Continuous operators play a critical role in functional analysis by ensuring stability and boundedness of transformations between normed spaces, facilitating the study of differential equations and optimization problems. Compact operators are essential in spectral theory and integral equations, as their properties allow the application of the Fredholm alternative and the analysis of eigenvalue distributions in infinite-dimensional spaces. Both operator types enable crucial advancements in solving partial differential equations and contribute significantly to operator theory and functional analysis frameworks.
Role in Solving Differential and Integral Equations
Continuous operators facilitate the stability and existence of solutions in differential and integral equations by ensuring boundedness and continuity across function spaces. Compact operators, characterized by their ability to map bounded sets to relatively compact sets, play a crucial role in applying the Fredholm theory, leading to the existence of eigenvalues and eigenfunctions that simplify solving integral equations. The compactness property often enables the use of spectral methods and iterative schemes, making compact operators essential in decomposing complex problems into solvable components.
Summary: Choosing Between Continuous and Compact Operators
Continuous operators guarantee bounded linear transformations between normed spaces, ensuring stability and general applicability in functional analysis. Compact operators, a subset of continuous operators, exhibit stronger properties by mapping bounded sets to relatively compact sets, which facilitates the analysis of spectral theory and integral equations. When choosing between continuous and compact operators, prioritize compact operators for problems requiring spectral decomposition and approximations, while continuous operators suit broader applications without compactness constraints.
Continuous operator Infographic
 libterm.com
libterm.com