Rank plays a crucial role in search engine optimization by determining the visibility and position of a webpage in search results. High ranking improves your site's chances of attracting relevant traffic and increases credibility among users. Explore the full article to discover effective strategies for boosting your website's rank.
Table of Comparison
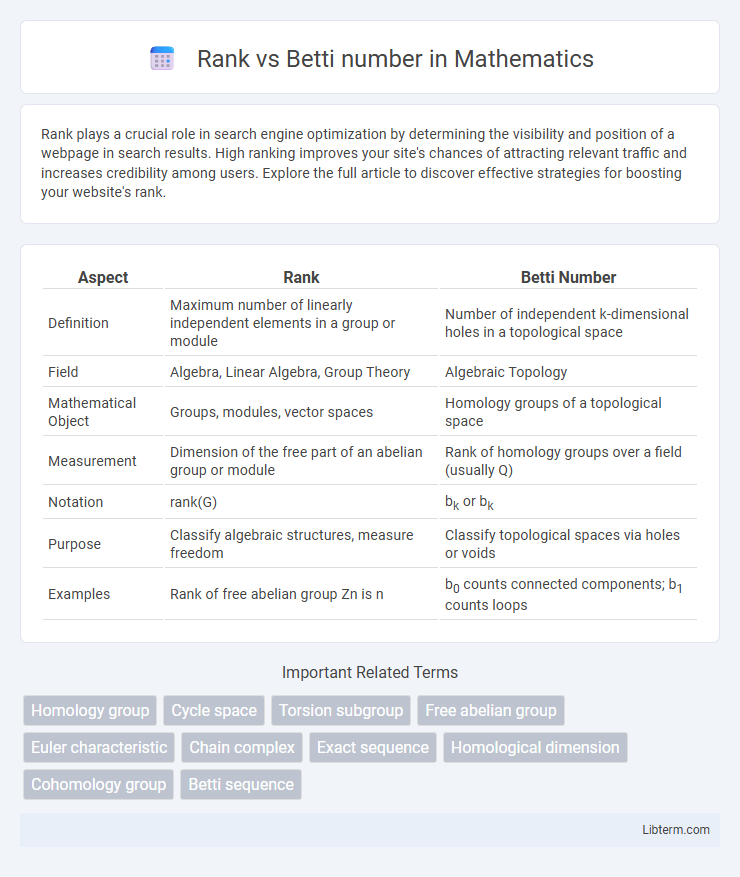
| Aspect | Rank | Betti Number |
|---|---|---|
| Definition | Maximum number of linearly independent elements in a group or module | Number of independent k-dimensional holes in a topological space |
| Field | Algebra, Linear Algebra, Group Theory | Algebraic Topology |
| Mathematical Object | Groups, modules, vector spaces | Homology groups of a topological space |
| Measurement | Dimension of the free part of an abelian group or module | Rank of homology groups over a field (usually Q) |
| Notation | rank(G) | bk or bk |
| Purpose | Classify algebraic structures, measure freedom | Classify topological spaces via holes or voids |
| Examples | Rank of free abelian group Zn is n | b0 counts connected components; b1 counts loops |
Introduction to Rank and Betti Number
Rank refers to the maximum number of linearly independent vectors in a vector space or matrix, serving as a fundamental measure of dimensionality and structural complexity. Betti numbers quantify topological features of a space, counting independent cycles at each dimension to describe the shape's connectivity and holes. Together, rank and Betti numbers provide critical insights into algebraic topology and linear algebra by linking algebraic properties with topological invariants.
Defining Rank in Algebra and Topology
Rank in algebra refers to the maximal number of linearly independent vectors in a vector space or the dimension of the image of a linear transformation, serving as a measure of its linear independence. In topology, rank often appears as the rank of homology groups, representing the number of independent cycles or holes in a given dimension. Betti numbers quantify these ranks by counting the independent topological features such as connected components, loops, and voids, providing a bridge between algebraic rank and topological invariants.
Understanding Betti Numbers in Topology
Betti numbers are fundamental invariants in algebraic topology that quantify the number of independent cycles or holes in various dimensions of a topological space, reflecting its intrinsic geometric structure. Unlike rank, which generally denotes the maximal number of linearly independent elements in algebraic structures such as groups or matrices, Betti numbers specifically measure the ranks of homology groups, thereby capturing topological features like connected components (Betti number 0), tunnels (Betti number 1), and voids (Betti number 2). Understanding Betti numbers enables the classification of spaces through their homological characteristics and facilitates computations in topological data analysis, manifold theory, and complex geometry.
Historical Development of Rank and Betti Number
Rank and Betti numbers originated from distinct mathematical disciplines, with rank initially arising in linear algebra to indicate the dimension of the image of a matrix or linear transformation. Betti numbers, introduced by Enrico Betti in the 19th century, emerged from algebraic topology to quantify the number of independent cycles or holes in topological spaces. The historical development of these concepts highlights their foundational roles in understanding algebraic structures and topological invariants, linking linear algebra with topology through homology theory.
Fundamental Differences Between Rank and Betti Number
Rank measures the maximum number of linearly independent vectors in a vector space or modules, reflecting the dimension of free components, whereas Betti numbers quantify the number of k-dimensional holes in a topological space, capturing its homological features. Rank is an algebraic invariant primarily used in linear algebra and module theory, while Betti numbers arise in algebraic topology to describe the connectivity and shape of spaces. Fundamental differences lie in their interpretations: rank relates to algebraic structure complexity, whereas Betti numbers reveal topological characteristics and the presence of cycles or voids.
Rank in Homology and Algebraic Structures
Rank in homology reflects the number of independent cycles in a topological space, serving as a fundamental measure of its structure by quantifying the free part of homology groups. Unlike Betti numbers, which specifically count the dimensions of homology groups over a field, rank extends to modules over rings, capturing torsion-free components in algebraic structures. This distinction emphasizes the rank's role in analyzing homological invariants beyond vector spaces, providing deeper insights into algebraic and topological properties.
Applications of Betti Numbers in Topological Data Analysis
Betti numbers quantify the number of independent k-dimensional holes in a topological space, serving as key invariants in algebraic topology. In topological data analysis (TDA), Betti numbers enable the characterization of complex data shapes by capturing connected components, loops, and voids within high-dimensional datasets. Their applications include identifying clusters, detecting cyclic structures in sensor networks, and analyzing the shape of data manifolds for pattern recognition and machine learning tasks.
Relationships and Interactions: Rank vs Betti Number
Rank and Betti numbers both measure topological features in algebraic topology but focus on different aspects; rank typically refers to the dimension of a homology group's free part, while Betti numbers quantify the number of independent cycles or holes in various dimensions. The first Betti number equals the rank of the first homology group, linking them directly in analyzing topological spaces. Interactions between rank and Betti numbers reveal structural properties of spaces, such as connectivity and the presence of handles or voids, essential for understanding topological invariants.
Real-World Examples Illustrating Rank and Betti Number
Rank and Betti numbers provide critical insights into the structure of complex systems such as social networks and biological data. In social network analysis, the rank of adjacency matrices measures the maximum number of independent connections, reflecting network robustness, while Betti numbers, derived from persistent homology, quantify topological features like connected components and loops, revealing community structures. Similarly, in neuroscience, Betti numbers help identify cycles in brain connectivity patterns, indicating functional pathways, whereas matrix rank evaluates signal redundancy and dimensionality reduction in neural data processing.
Summary: Choosing Between Rank and Betti Number
Rank quantifies the dimension of a vector space or module, providing a measure of linear independence and structural size in algebraic contexts. Betti numbers represent topological invariants that count the maximum number of cuts or holes in varying dimensions, capturing the shape's intrinsic connectivity. Choosing between rank and Betti number depends on whether the focus is algebraic structures or topological features, with rank emphasizing algebraic dimension and Betti numbers highlighting topological complexity.
Rank Infographic
 libterm.com
libterm.com