A finite group is a mathematical structure consisting of a set equipped with an operation that combines any two elements to form a third, adhering to closure, associativity, identity, and invertibility properties, with the set containing a limited number of elements. These groups are fundamental in abstract algebra and have applications across symmetry analysis, cryptography, and particle physics. Explore the rest of the article to deepen your understanding of finite groups and their significance.
Table of Comparison
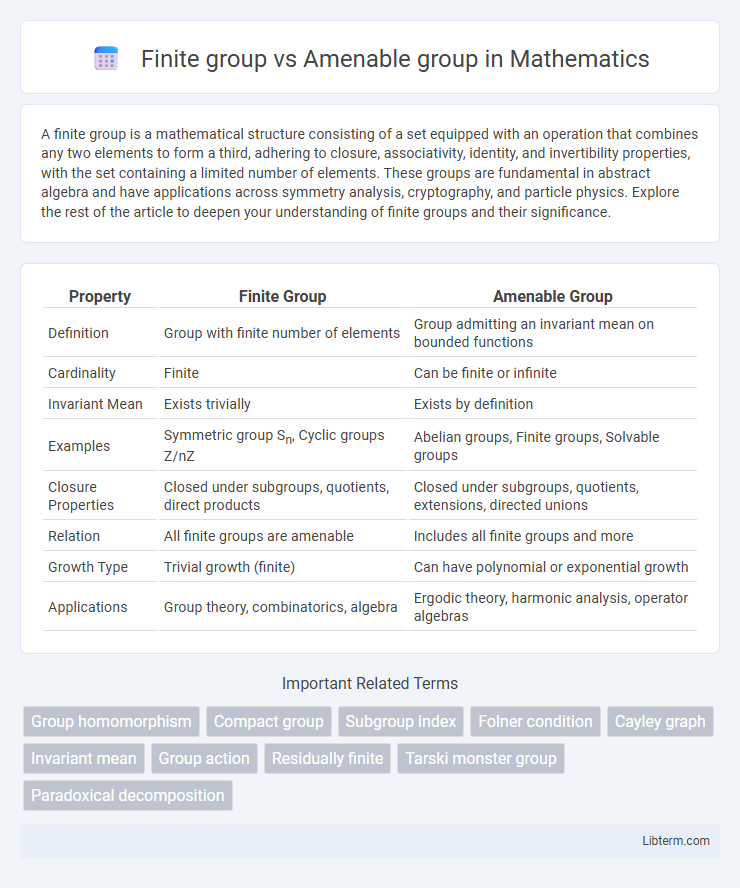
| Property | Finite Group | Amenable Group |
|---|---|---|
| Definition | Group with finite number of elements | Group admitting an invariant mean on bounded functions |
| Cardinality | Finite | Can be finite or infinite |
| Invariant Mean | Exists trivially | Exists by definition |
| Examples | Symmetric group Sn, Cyclic groups Z/nZ | Abelian groups, Finite groups, Solvable groups |
| Closure Properties | Closed under subgroups, quotients, direct products | Closed under subgroups, quotients, extensions, directed unions |
| Relation | All finite groups are amenable | Includes all finite groups and more |
| Growth Type | Trivial growth (finite) | Can have polynomial or exponential growth |
| Applications | Group theory, combinatorics, algebra | Ergodic theory, harmonic analysis, operator algebras |
Introduction to Finite and Amenable Groups
Finite groups are algebraic structures consisting of a limited number of elements with a group operation satisfying closure, associativity, identity, and invertibility; these groups are fundamental in symmetry analysis and combinatorial contexts. Amenable groups extend the concept by allowing infinite elements but possess an invariant mean, enabling the application of averaging techniques in harmonic analysis and ergodic theory. The key distinction lies in finiteness versus amenability, where amenable groups generalize finite and abelian groups through properties like Folner conditions and paradoxical decompositions avoidance.
Key Definitions: Finite Groups Explained
Finite groups are algebraic structures consisting of a set with a finite number of elements equipped with a binary operation satisfying group axioms: closure, associativity, identity, and invertibility. Amenable groups, by contrast, encompass a broader class including finite groups and infinite groups possessing an invariant mean, reflecting a specialized property related to averaging and measure theory. Understanding finite groups is fundamental as they serve as essential examples within the larger category of amenable groups, highlighting the foundational role finite order and symmetry play in abstract algebra.
Amenable Groups: Meaning and Origins
Amenable groups are algebraic structures characterized by having an invariant mean, enabling the extension of finite averaging concepts to infinite groups. Originating from John von Neumann's work in the 1920s to address paradoxes in measure theory, amenable groups generalize properties of finite and abelian groups by allowing a finitely additive, translation-invariant probability measure. This concept plays a crucial role in ergodic theory, harmonic analysis, and geometric group theory, distinguishing amenable groups from non-amenable ones via properties like the Folner condition.
Core Properties of Finite Groups
Finite groups possess fundamental core properties such as closure, associativity, identity, and inverses within a limited set, ensuring every element has a finite order. Their structure guarantees that all subgroups and quotient groups are also finite, enabling comprehensive algebraic analysis. Unlike amenable groups, finite groups inherently satisfy invariant mean existence due to their compact and discrete nature.
Essential Properties of Amenable Groups
Amenable groups are characterized by the existence of an invariant mean, which ensures a finitely additive probability measure invariant under group action. Unlike finite groups, which trivially possess amenability due to their limited cardinality, amenable groups include infinite examples such as abelian groups and solvable groups. Essential properties of amenable groups include closure under taking subgroups, quotients, extensions, and direct limits, reflecting their flexibility and significance in group theory and harmonic analysis.
Overlaps and Differences: Finite vs Amenable
Finite groups are inherently amenable due to their existence of a finitely additive probability measure invariant under group action, while amenable groups extend beyond finite cases to include infinite groups like abelian and solvable groups. The primary overlap lies in the presence of invariant means, but finite groups have strictly limited cardinality, whereas amenable groups feature more complex structures allowing infinite elements. Differences arise in their algebraic properties and applications, with finite groups often analyzed through classical group theory and amenable groups studied in functional analysis and ergodic theory.
Examples of Finite Groups in Mathematics
Finite groups, such as the symmetric group S_n consisting of all permutations of n elements, serve as fundamental examples in group theory and illustrate properties like closure, associativity, and invertibility. Amenable groups include all finite groups, highlighting that every finite group carries an invariant mean due to its limited size and structure. The finiteness ensures that these groups are trivially amenable, contrasting with many infinite groups where amenability depends on more complex criteria.
Typical Examples of Amenable Groups
Typical examples of amenable groups include finite groups, abelian groups, and solvable groups, all characterized by the existence of an invariant mean on bounded functions. Finite groups are trivially amenable since any averaging process is finite and well-defined, whereas infinite amenable groups like the integers under addition exhibit properties such as Folner sequences that approximate invariant means. Non-amenable groups, such as free groups with two or more generators, contrast sharply by lacking these averaging properties.
Why Non-Amenable Groups Matter
Non-amenable groups lack an invariant mean, distinguishing them sharply from finite or amenable groups that allow such averaging properties. This difference profoundly impacts areas like geometric group theory and functional analysis, where non-amenable groups exhibit paradoxical decompositions and fail fixed-point properties. Understanding non-amenable groups is crucial for exploring phenomena in ergodic theory, the theory of von Neumann algebras, and the study of expander graphs, which have applications in computer science and network theory.
Applications and Relevance in Modern Math
Finite groups provide foundational structure in algebra with direct applications in symmetry analysis, cryptography, and coding theory due to their discrete and well-understood nature. Amenable groups, characterized by invariant means, play a crucial role in ergodic theory, operator algebras, and geometric group theory, enabling breakthroughs in understanding group actions and measurable dynamics. The distinction between finite and amenable groups influences the development of harmonic analysis on groups and the study of group von Neumann algebras, impacting fields such as probability, statistical mechanics, and combinatorial group theory.
Finite group Infographic
 libterm.com
libterm.com