A group consists of individuals who share common interests, goals, or characteristics, fostering collaboration and connection. Understanding group dynamics can enhance communication and productivity within your team. Explore the rest of the article to learn how effective group management can benefit your personal and professional life.
Table of Comparison
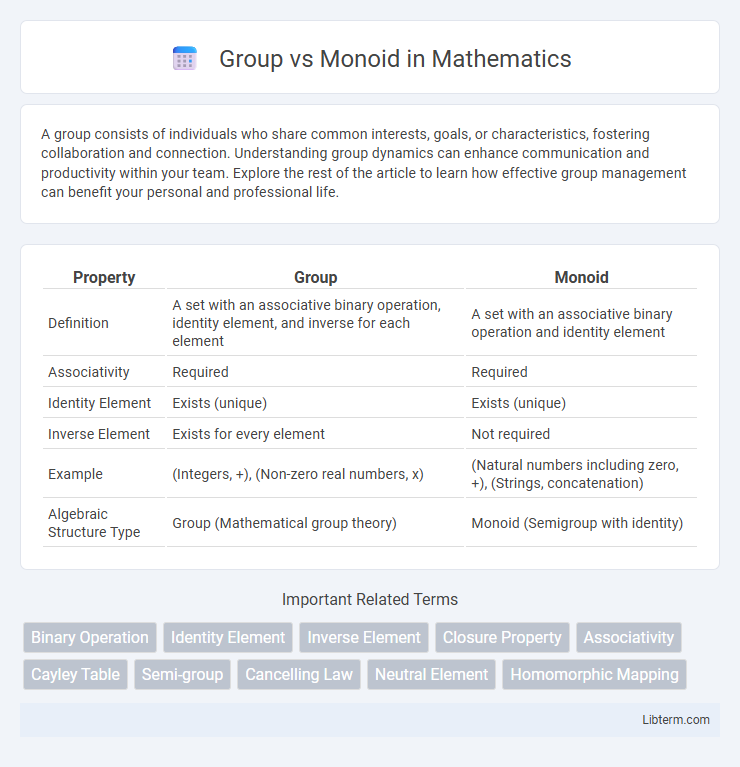
| Property | Group | Monoid |
|---|---|---|
| Definition | A set with an associative binary operation, identity element, and inverse for each element | A set with an associative binary operation and identity element |
| Associativity | Required | Required |
| Identity Element | Exists (unique) | Exists (unique) |
| Inverse Element | Exists for every element | Not required |
| Example | (Integers, +), (Non-zero real numbers, x) | (Natural numbers including zero, +), (Strings, concatenation) |
| Algebraic Structure Type | Group (Mathematical group theory) | Monoid (Semigroup with identity) |
Introduction to Algebraic Structures
A group is an algebraic structure consisting of a set equipped with an associative binary operation, an identity element, and inverses for every element, ensuring closure under the operation. A monoid also features an associative binary operation and an identity element but does not require each element to have an inverse, making groups a special case of monoids. Both structures play a foundational role in abstract algebra, with groups offering symmetrical properties useful in areas such as symmetry analysis and monoids applicable in computer science and formal language theory.
Defining Groups: Essential Properties
Groups are algebraic structures defined by a set equipped with a binary operation that is associative, has an identity element, and where every element has an inverse. In contrast, monoids require only associativity and an identity element, without necessitating inverses for each element. The presence of inverses for all group elements enables more robust algebraic manipulations and symmetry operations compared to monoids.
Understanding Monoids: Key Characteristics
Monoids are algebraic structures consisting of a set equipped with an associative binary operation and an identity element. Every group is a monoid, but monoids do not require the existence of inverse elements for every element. Key characteristics of monoids include closure under the operation, associativity, and the presence of a neutral identity element, distinguishing them from groups which also require invertibility.
Group vs Monoid: Core Differences
Groups and monoids are algebraic structures with a single associative binary operation and an identity element, but groups require every element to have an inverse while monoids do not. This key difference means groups guarantee invertibility, enabling solutions to equations like a * x = e, which monoids may lack. The presence of inverses in groups allows for more robust algebraic properties used in various mathematical and computational contexts.
Identity Element in Groups and Monoids
The identity element in a group is a unique element that, when combined with any group element, leaves it unchanged, fulfilling the identity law in group theory. In monoids, the identity element also exists and serves the same purpose, ensuring closure and associativity within the set under a binary operation. Unlike groups, monoids do not require every element to have an inverse, making the identity element crucial for maintaining the structure's operation without demanding invertibility.
Associativity in Group and Monoid Operations
Groups and monoids both require associativity in their binary operations, meaning the operation must satisfy (a * b) * c = a * (b * c) for all elements a, b, c in the set. This associativity ensures consistent grouping of operations without altering the outcome, which is fundamental in abstract algebra. While monoids guarantee an associative operation along with an identity element, groups extend this by additionally requiring every element to have an inverse, preserving the associative property throughout all operations.
Inverses: Unique to Groups
Groups guarantee the existence of an inverse element for every member, ensuring that each element combined with its inverse yields the identity element. In contrast, monoids do not require inverses, only an associative binary operation and an identity element are needed. This uniqueness of inverses in groups enables solving equations within the structure, a property absent in monoids.
Real-world Examples of Groups and Monoids
Groups appear commonly in cryptography, where the set of integers modulo a prime number under addition forms an abelian group essential for encryption algorithms. Monoids emerge naturally in computer science through string concatenation, where the set of all strings over an alphabet with concatenation as the operation and the empty string as the identity element models a monoid. Rotation symmetries of a square illustrate group structures with invertible elements, while file system paths concatenated to build directory strings exemplify monoids without requiring inverses.
Applications in Mathematics and Computer Science
Groups provide a foundational structure for symmetry analysis in algebra and physics, enabling the study of transformations that preserve certain properties. Monoids generalize groups by relaxing invertibility, making them essential in computer science for modeling computations such as string concatenation and state transitions in automata theory. Both structures play crucial roles in category theory and functional programming, where monoids underpin aggregation operations and groups facilitate reversible processes.
Summary: Choosing Between Group and Monoid
Groups require every element to have an inverse, enabling solutions to equations and symmetrical operations, making them ideal for mathematical structures needing reversibility. Monoids only require an associative binary operation with an identity element, offering simpler models for processes where inversion isn't necessary, such as string concatenation or state transitions. Selecting between group and monoid hinges on whether invertibility of elements is essential for the problem domain or if closure and identity suffice for the computational or algebraic context.
Group Infographic
 libterm.com
libterm.com