A manifold is a mathematical space that locally resembles Euclidean space and allows complex structures to be analyzed with calculus and geometry. Manifolds play a critical role in fields such as physics, computer graphics, and differential geometry. Explore the rest of the article to deepen your understanding of manifolds and their wide-ranging applications.
Table of Comparison
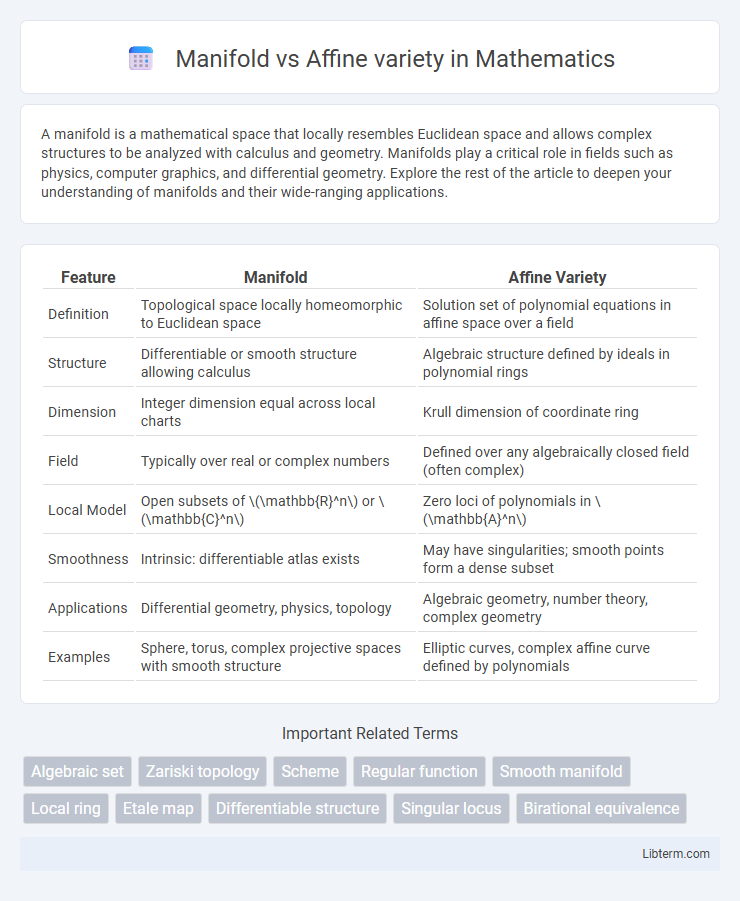
| Feature | Manifold | Affine Variety |
|---|---|---|
| Definition | Topological space locally homeomorphic to Euclidean space | Solution set of polynomial equations in affine space over a field |
| Structure | Differentiable or smooth structure allowing calculus | Algebraic structure defined by ideals in polynomial rings |
| Dimension | Integer dimension equal across local charts | Krull dimension of coordinate ring |
| Field | Typically over real or complex numbers | Defined over any algebraically closed field (often complex) |
| Local Model | Open subsets of \(\mathbb{R}^n\) or \(\mathbb{C}^n\) | Zero loci of polynomials in \(\mathbb{A}^n\) |
| Smoothness | Intrinsic: differentiable atlas exists | May have singularities; smooth points form a dense subset |
| Applications | Differential geometry, physics, topology | Algebraic geometry, number theory, complex geometry |
| Examples | Sphere, torus, complex projective spaces with smooth structure | Elliptic curves, complex affine curve defined by polynomials |
Introduction to Manifolds and Affine Varieties
Manifolds are topological spaces that locally resemble Euclidean space and support calculus, making them fundamental in differential geometry and topology. Affine varieties are algebraic sets defined as the solution loci of systems of polynomial equations over algebraically closed fields, forming the core objects in algebraic geometry. The key distinction lies in manifolds being smooth and continuous structures, while affine varieties are rigid algebraic sets characterized by polynomial relations.
Fundamental Definitions
A manifold is a topological space that locally resembles Euclidean space and supports smooth differentiable structures, enabling calculus on curved surfaces. An affine variety is an algebraic geometric object defined as the zero set of polynomial equations in affine space, characterized by algebraic rather than smooth structures. While manifolds emphasize smoothness and local coordinate charts, affine varieties focus on solutions to polynomial equations and algebraic properties.
Algebraic Structure Overview
Manifolds are smooth topological spaces locally resembling Euclidean space, emphasizing differential structures without inherent algebraic equations. Affine varieties are zero sets of polynomial equations over a field, defined within algebraic geometry and equipped with a coordinate ring that encodes their algebraic structure. The key algebraic distinction lies in manifolds lacking a global ring of functions with polynomial constraints, whereas affine varieties possess a coordinate ring forming a finitely generated algebra over a base field.
Geometric Properties
Manifolds are topological spaces locally resembling Euclidean space, emphasizing smooth structure enabling calculus, while affine varieties are solution sets of polynomial equations studied in algebraic geometry with a strong algebraic and Zariski topology. Geometrically, manifolds have differentiable structures with tangent spaces defined at every point, whereas affine varieties carry algebraic structures allowing singularities and are studied via coordinate rings and algebraic morphisms. The smoothness and local triviality in manifolds contrast with the algebraic constraints and potential singular points inherent in affine varieties, highlighting different approaches to geometry in differential and algebraic contexts.
Local vs Global Descriptions
Manifolds are locally similar to Euclidean space, allowing for smooth coordinate charts that enable calculus and differential topology techniques, while affine varieties rely on polynomial equations providing a global algebraic description. The local structure of a manifold emphasizes differentiability and local homeomorphisms, whereas an affine variety encapsulates global properties through algebraic sets defined over fields. This distinction highlights that manifolds prioritize smooth local patches, whereas affine varieties focus on globally defined algebraic geometry.
Examples of Manifolds and Affine Varieties
The 2-dimensional sphere \( S^2 = \{(x,y,z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1\} \) serves as a classic example of a smooth manifold that is not affine. In contrast, the affine variety defined by the zero set of polynomials such as \( V(f) = \{(x,y) \in \mathbb{C}^2 \mid f(x,y) = y^2 - x^3 - x = 0\} \) exemplifies an algebraic variety with a coordinate ring structure. Complex projective spaces like \( \mathbb{CP}^n \) provide additional examples of manifolds, while affine varieties arise naturally as solution sets to systems of polynomial equations over algebraically closed fields.
Differences in Coordinate Systems
Manifolds use charts and atlases consisting of homeomorphisms to Euclidean spaces for local coordinate systems, emphasizing smooth transitions between neighborhoods. Affine varieties employ coordinate rings derived from polynomial functions, defining coordinates algebraically via the vanishing sets of polynomial ideals. This fundamental distinction reflects the analytic flexibility of manifolds versus the rigid algebraic structure inherent in affine varieties' coordinate systems.
Smoothness and Singularity Considerations
A manifold is a topological space that locally resembles Euclidean space and is inherently smooth, ensuring each point has a neighborhood diffeomorphic to an open subset of \(\mathbb{R}^n\). An affine variety, defined as the zero set of polynomial equations in affine space, may contain singularities where the Jacobian matrix of defining polynomials drops rank, indicating non-smooth points. Smoothness of an affine variety is characterized by the regularity condition that the dimension of the tangent space equals the dimension of the variety at every point, while singularities correspond to points failing this condition, differentiating it from the uniform smoothness of manifolds.
Applications in Mathematics and Science
Manifolds provide the foundational framework for differential geometry, enabling the study of smooth structures and curvature essential in physics, particularly in general relativity and classical mechanics. Affine varieties, fundamental in algebraic geometry, allow for the exploration of polynomial solutions and are crucial in number theory, coding theory, and cryptography. Both structures facilitate modeling complex systems, with manifolds emphasizing smoothness and tangential properties, while affine varieties focus on algebraic equations and their geometric interpretations.
Summary: Key Distinctions and Implications
Manifolds are topological spaces that locally resemble Euclidean space and support smooth structures for differential calculus, while affine varieties are fundamental objects in algebraic geometry defined as the zero sets of polynomial equations over algebraically closed fields. The key distinction lies in manifolds emphasizing smooth structures and local Euclidean properties, whereas affine varieties emphasize algebraic structure and polynomial relations. This difference impacts their applications: manifolds serve in differential geometry and physics, while affine varieties are central to solving polynomial equations and algebraic geometry problems.
Manifold Infographic
 libterm.com
libterm.com