Norm defines a standard or rule that guides behavior and expectations within a group or society, ensuring consistency and predictability. Understanding norms helps You navigate social interactions and align with community values effectively. Explore the rest of the article to discover how norms influence everyday life and decision-making processes.
Table of Comparison
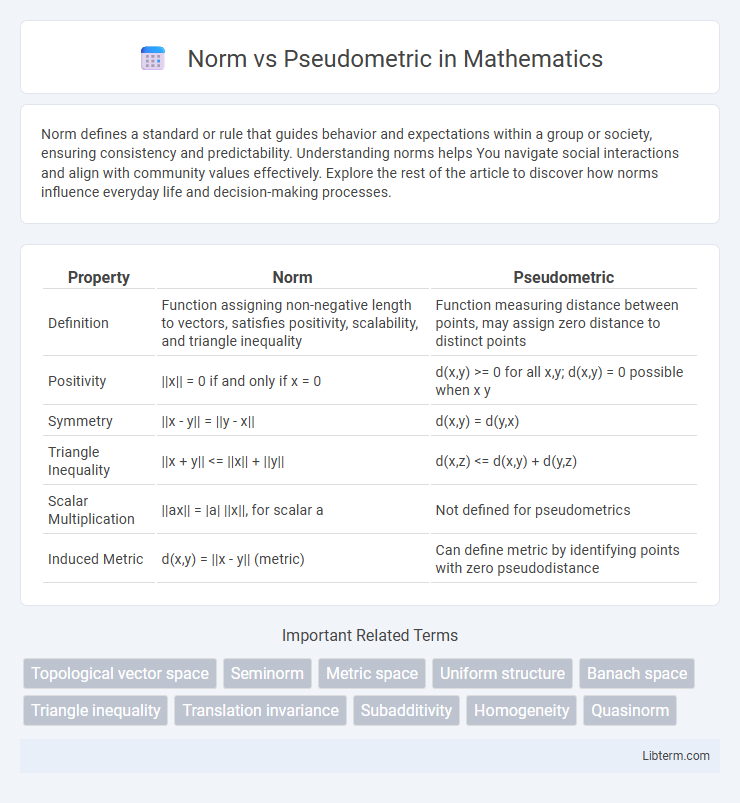
| Property | Norm | Pseudometric |
|---|---|---|
| Definition | Function assigning non-negative length to vectors, satisfies positivity, scalability, and triangle inequality | Function measuring distance between points, may assign zero distance to distinct points |
| Positivity | ||x|| = 0 if and only if x = 0 | d(x,y) >= 0 for all x,y; d(x,y) = 0 possible when x y |
| Symmetry | ||x - y|| = ||y - x|| | d(x,y) = d(y,x) |
| Triangle Inequality | ||x + y|| <= ||x|| + ||y|| | d(x,z) <= d(x,y) + d(y,z) |
| Scalar Multiplication | ||ax|| = |a| ||x||, for scalar a | Not defined for pseudometrics |
| Induced Metric | d(x,y) = ||x - y|| (metric) | Can define metric by identifying points with zero pseudodistance |
Introduction to Norms and Pseudometrics
Norms quantify vector lengths in vector spaces by assigning non-negative scalar values that satisfy positivity, scalability, and the triangle inequality, ensuring a structured measurement of magnitude. Pseudometrics generalize metrics by allowing zero distance between distinct points, defining a relaxed form of distance in spaces where traditional metric properties may not hold. Understanding norms and pseudometrics is fundamental in functional analysis and topology for characterizing space structure and continuity.
Fundamental Definitions: Norms vs Pseudometrics
A norm is a function on a vector space that assigns a non-negative length to each vector, satisfying positivity, scalability, and the triangle inequality, ensuring the norm of a vector is zero only if the vector itself is zero. A pseudometric, defined on a set, measures distance between elements but allows distinct points to have zero distance, relaxing the definiteness property required by metrics. The key difference lies in a norm enforcing a strict zero condition only at the zero vector, while a pseudometric permits zero distance between different points, reflecting their respective roles in vector spaces and general metric spaces.
Key Properties of Norms
Norms satisfy positivity, ensuring the norm of any vector is non-negative and zero if and only if the vector itself is zero, while pseudometrics allow zero distance between distinct points. Norms exhibit absolute scalability, meaning the norm of a scalar multiple of a vector equals the absolute value of the scalar times the norm of the vector, a property not necessarily mirrored by pseudometrics. The triangle inequality holds for both, guaranteeing that the norm or pseudometric distance between two points is bounded by the sum of distances through an intermediate point, but norms integrate this with vector space structure, emphasizing linearity and homogeneity.
Essential Characteristics of Pseudometrics
Pseudometrics differ from norms by allowing distinct points to have zero distance, thus relaxing the identity of indiscernibles property found in metrics. Essential characteristics of pseudometrics include non-negativity, symmetry, and the triangle inequality, while permitting d(x, y) = 0 for x y. This flexibility enables their use in spaces where equivalence classes of points are formed, making them crucial in functional analysis and topology.
Core Differences Between Norms and Pseudometrics
Norms assign a non-negative length to vectors, satisfying positive definiteness, scaling, and the triangle inequality, while pseudometrics measure distance between points but allow zero distance between distinct points, violating positive definiteness. A norm induces a metric by defining distance as the norm of the difference between vectors, but a pseudometric may not arise from a norm due to relaxed restrictions. Core differences include the strict requirement of positive definiteness in norms, ensuring distinct vectors have positive length, unlike pseudometrics where distinct points can have zero distance.
Examples of Norms in Mathematics
Common examples of norms in mathematics include the Euclidean norm, defined as the square root of the sum of the squares of vector components, and the Manhattan norm, calculated as the sum of the absolute values of the components. These norms satisfy the properties of positivity, scalability, and the triangle inequality, distinguishing them from pseudometrics, which may lack strict positivity. Norms are fundamental in functional analysis and vector spaces, providing measures of vector length and distance essential for convergence and stability analysis.
Illustrative Examples of Pseudometrics
A pseudometric generalizes the concept of a norm by relaxing the requirement that the distance between distinct points must be positive, allowing distinct elements to have a zero distance. For example, in the space of continuous functions on [0,1], the pseudometric defined by the integral of the absolute difference weighted on a subset of the domain can measure function similarity while ignoring differences outside that subset. Another illustrative pseudometric is the edit distance between strings, where transformations with zero cost on specific substrings can yield zero pseudodistance between different strings, distinguishing it from a true metric or norm.
Applications in Functional Analysis
Norms provide a framework for measuring vector lengths and distances in normed vector spaces, essential for defining convergence, continuity, and boundedness in functional analysis. Pseudometrics generalize metrics by allowing distinct points to have zero distance, useful in identifying equivalence classes and studying quotient spaces in function spaces. Applications include analyzing operator norms, Banach space theory, and the structure of spaces of equivalence classes arising in distribution theory and Sobolev spaces.
Practical Significance in Modern Mathematics
Norms establish a rigorous framework for measuring vector magnitude, ensuring properties like definiteness and the triangle inequality that enable robust geometric interpretations in functional analysis and optimization. Pseudometrics relax the definiteness condition, allowing zero distances between distinct points, which proves crucial in topology and computer science for modeling indistinguishable states or fuzzy equivalences. The practical significance lies in using norms to guarantee convergence and stability in numerical algorithms, while pseudometrics facilitate flexible distance measures in abstract spaces where exact equality is either impossible or unnecessary.
Summary: Choosing Between Norms and Pseudometrics
Norms provide a structured way to measure vector magnitude with properties like positivity, scalability, and the triangle inequality, ensuring meaningful distance interpretations in vector spaces. Pseudometrics relax the requirement of distinctness, allowing zero distance between different points, which is useful in applications involving equivalence classes or fuzzy similarity measures. Selecting between norms and pseudometrics depends on the need for strict identity distinctions versus flexibility in measuring generalized distances.
Norm Infographic
 libterm.com
libterm.com