Pointwise convergence occurs when a sequence of functions converges at each individual point within a domain, meaning for every point, the sequence approaches a specific value as it progresses. This type of convergence is crucial in understanding the behavior of function sequences and their limits in mathematical analysis. Explore the rest of the article to learn how pointwise convergence contrasts with uniform convergence and its implications in various applications.
Table of Comparison
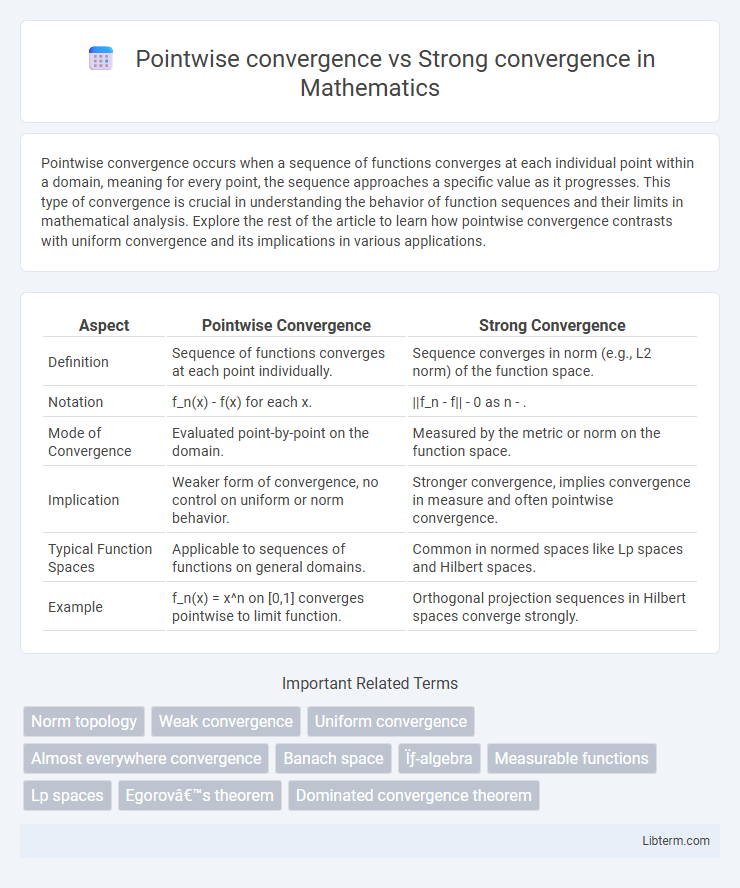
| Aspect | Pointwise Convergence | Strong Convergence |
|---|---|---|
| Definition | Sequence of functions converges at each point individually. | Sequence converges in norm (e.g., L2 norm) of the function space. |
| Notation | f_n(x) - f(x) for each x. | ||f_n - f|| - 0 as n - . |
| Mode of Convergence | Evaluated point-by-point on the domain. | Measured by the metric or norm on the function space. |
| Implication | Weaker form of convergence, no control on uniform or norm behavior. | Stronger convergence, implies convergence in measure and often pointwise convergence. |
| Typical Function Spaces | Applicable to sequences of functions on general domains. | Common in normed spaces like Lp spaces and Hilbert spaces. |
| Example | f_n(x) = x^n on [0,1] converges pointwise to limit function. | Orthogonal projection sequences in Hilbert spaces converge strongly. |
Introduction to Sequence Convergence in Analysis
Pointwise convergence occurs when a sequence of functions converges to a limit function at each individual point within the domain, allowing variations in the rate of convergence across different points. Strong convergence, often synonymous with convergence in norm within function spaces like \( L^p \), demands that the sequence converges with respect to a chosen norm, ensuring uniform control over the entire domain. Understanding these modes of convergence is fundamental in analysis, as they influence continuity, integration, and the stability of functional limits in various mathematical contexts.
Definition of Pointwise Convergence
Pointwise convergence of a sequence of functions occurs when, for every fixed point in the domain, the sequence of function values converges to the value of the limiting function. Formally, a sequence \((f_n)\) converges pointwise to \(f\) if for every \(x\), \(\lim_{n \to \infty} f_n(x) = f(x)\). This type of convergence contrasts with strong convergence, which requires convergence in a norm or metric sense across the entire function space.
Definition of Strong (Norm) Convergence
Strong convergence, also known as norm convergence, occurs when a sequence of functions \( \{f_n\} \) converges to a function \( f \) in the norm of a given function space, typically meaning \( \|f_n - f\| \to 0 \) as \( n \to \infty \). This type of convergence ensures that the functions \( f_n \) get arbitrarily close to \( f \) in terms of the overall size or magnitude measured by the norm, not just at individual points. Strong convergence implies pointwise convergence almost everywhere, but pointwise convergence does not guarantee strong convergence.
Key Differences Between Pointwise and Strong Convergence
Pointwise convergence refers to a sequence of functions converging to a limit function at each individual point in the domain, whereas strong convergence involves convergence in norm within a function space, such as L2 or Hilbert spaces. The key difference lies in the mode of convergence: pointwise convergence is concerned with function values converging almost everywhere, while strong convergence requires the entire sequence to converge in the norm topology, implying uniform control over the entire domain. Strong convergence guarantees more robust approximation properties and stability compared to pointwise convergence, which can fail to preserve integrability or continuity.
Examples Illustrating Pointwise Convergence
Pointwise convergence occurs when a sequence of functions \( f_n(x) \) converges to a function \( f(x) \) for each fixed \( x \) in the domain, such as the sequence \( f_n(x) = x^n \) on the interval \([0,1)\), which converges pointwise to the function \( f(x) \) that is zero on \([0,1)\) and one at \( x=1 \). Another classic example is the sequence of functions defined as \( f_n(x) = \frac{x}{n} \), which converges pointwise to the zero function on any domain. These examples demonstrate pointwise convergence by showing how convergence is evaluated separately for each point, unlike strong convergence which requires convergence in a normed space and implies uniform or \(L^p\)-norm convergence.
Examples Demonstrating Strong Convergence
Strong convergence in Hilbert spaces means a sequence of vectors converges with respect to the norm, ensuring the norm of their difference tends to zero, unlike pointwise convergence which only guarantees convergence at each coordinate. An example is the sequence \( x_n = \frac{1}{n}e_1 \) in \( \ell^2 \), where \( e_1 \) is the first standard basis vector; this sequence strongly converges to the zero vector since \( \|x_n - 0\| = \frac{1}{n} \to 0 \). Another example is the partial sums of Fourier series in \( L^2 \) spaces, which strongly converge to the function when the series is square integrable, highlighting strong convergence in function spaces beyond mere pointwise limits.
Implications in Functional Analysis
Pointwise convergence of a sequence of functions guarantees convergence at each individual point, while strong convergence (norm convergence) ensures convergence in the normed space, reflecting uniform control over the entire domain. In functional analysis, strong convergence implies pointwise convergence, but pointwise convergence does not necessarily imply strong convergence, impacting stability and continuity of operators. This distinction is crucial for spectral theory, operator approximation, and understanding compactness in Banach and Hilbert spaces.
When Does Pointwise Convergence Imply Strong Convergence?
Pointwise convergence implies strong convergence primarily in finite-dimensional normed spaces where norms are equivalent and limit preservation is uniform. In infinite-dimensional spaces, pointwise convergence of a sequence of functions or operators generally does not guarantee strong convergence due to potential lack of norm control. Strong convergence requires that the norm of the difference tends to zero, a condition stronger than mere pointwise convergence of values at each point.
Applications in Real-World Mathematical Contexts
Pointwise convergence is essential in analyzing function sequences in numerical methods, where evaluating limits at individual points ensures algorithm stability and accuracy. Strong convergence, crucial in functional analysis and optimization, guarantees norm convergence in Hilbert or Banach spaces, enabling reliable solutions in signal processing and machine learning. Applications in partial differential equations often leverage strong convergence for proving stability of solutions, while pointwise convergence aids in constructing approximations in computational methods.
Conclusion: Choosing the Right Type of Convergence
Pointwise convergence suits scenarios where function values at each individual point must converge, often used in analysis of sequences of functions with variable limits. Strong convergence, characterized by convergence in norm, provides a more robust framework ensuring overall stability and is essential in functional analysis and applications requiring quantitative error control. Selecting between pointwise and strong convergence depends on the desired precision and the context, with strong convergence preferred for guaranteeing uniform error bounds and pointwise convergence sufficient for localized behavior study.
Pointwise convergence Infographic
 libterm.com
libterm.com