Singular Value Decomposition (SVD) is a powerful matrix factorization technique widely used in data science, machine learning, and signal processing. It decomposes a matrix into three components, revealing intrinsic patterns and reducing dimensionality while preserving important information. Explore the rest of the article to understand how SVD can enhance your data analysis and modeling projects.
Table of Comparison
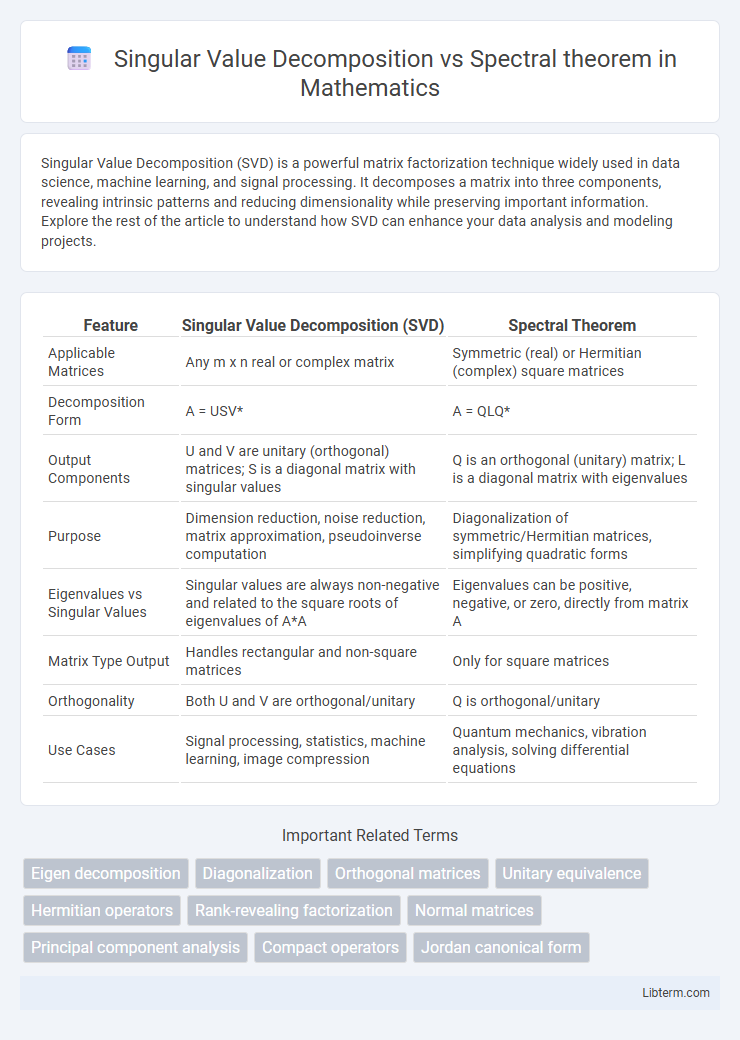
| Feature | Singular Value Decomposition (SVD) | Spectral Theorem |
|---|---|---|
| Applicable Matrices | Any m x n real or complex matrix | Symmetric (real) or Hermitian (complex) square matrices |
| Decomposition Form | A = USV* | A = QLQ* |
| Output Components | U and V are unitary (orthogonal) matrices; S is a diagonal matrix with singular values | Q is an orthogonal (unitary) matrix; L is a diagonal matrix with eigenvalues |
| Purpose | Dimension reduction, noise reduction, matrix approximation, pseudoinverse computation | Diagonalization of symmetric/Hermitian matrices, simplifying quadratic forms |
| Eigenvalues vs Singular Values | Singular values are always non-negative and related to the square roots of eigenvalues of A*A | Eigenvalues can be positive, negative, or zero, directly from matrix A |
| Matrix Type Output | Handles rectangular and non-square matrices | Only for square matrices |
| Orthogonality | Both U and V are orthogonal/unitary | Q is orthogonal/unitary |
| Use Cases | Signal processing, statistics, machine learning, image compression | Quantum mechanics, vibration analysis, solving differential equations |
Introduction to Singular Value Decomposition and Spectral Theorem
Singular Value Decomposition (SVD) factors any mxn matrix into USV*, where U and V are orthogonal matrices and S is a diagonal matrix with non-negative singular values, enabling dimensionality reduction and noise filtering. The Spectral Theorem states that every normal matrix can be diagonalized by a unitary matrix, providing eigenvalues and eigenvectors that reveal intrinsic properties of linear transformations. While SVD applies to all matrices, the Spectral Theorem specifically addresses normal operators, establishing foundational tools for matrix analysis and applications in data science, engineering, and quantum mechanics.
Mathematical Foundations and Definitions
Singular Value Decomposition (SVD) factorizes any m-by-n matrix A into USV*, where U and V are orthogonal matrices and S is a diagonal matrix with non-negative singular values, providing a robust tool for analyzing linear transformations beyond square matrices. The Spectral Theorem applies specifically to normal matrices, guaranteeing diagonalization via unitary matrices and enabling eigenvalue decomposition with orthonormal eigenvectors, thus revealing intrinsic matrix properties. While SVD generalizes matrix factorization to all matrices including rectangular ones, the Spectral Theorem is fundamental for understanding symmetric, Hermitian, and normal matrices through eigenvalues and eigenvectors.
Applicability to Different Types of Matrices
Singular Value Decomposition (SVD) applies to any m-by-n matrix, including non-square and non-symmetric matrices, providing a robust factorization into unitary matrices and a diagonal matrix of singular values. In contrast, the Spectral Theorem specifically applies to normal matrices, including symmetric (real) or Hermitian (complex) square matrices, enabling diagonalization via an orthonormal eigenbasis. SVD's broader applicability makes it essential for diverse matrix types in data compression, noise reduction, and system analysis, while the Spectral Theorem is crucial for understanding the eigenstructure of normal operators in functional analysis and quantum mechanics.
Geometric Interpretation
Singular Value Decomposition (SVD) geometrically represents any matrix as a combination of rotations and scalings, decomposing it into orthogonal matrices and a diagonal matrix of singular values that describe axis stretching. The Spectral Theorem applies specifically to normal matrices, illustrating geometric transformation through eigenvectors that form an orthonormal basis, with eigenvalues representing scale factors along these directions. While SVD captures both rotation and scaling in arbitrary matrices, the Spectral Theorem reveals intrinsic geometric properties by diagonalizing symmetric or normal matrices via an orthonormal eigenbasis.
Eigenvalues and Singular Values: Key Differences
Singular Value Decomposition (SVD) decomposes any mxn matrix into orthogonal matrices and a diagonal matrix containing singular values, which are the square roots of eigenvalues of the matrix multiplied by its transpose. The Spectral Theorem applies specifically to normal matrices, ensuring diagonalization via eigenvalues and eigenvectors with eigenvalues representing the matrix's intrinsic properties. Singular values are always non-negative and provide insight into matrix rank and stability, while eigenvalues can be complex and indicate matrix behavior in terms of directions and invariant subspaces.
Computational Methods and Complexity
Singular Value Decomposition (SVD) and the Spectral Theorem both decompose matrices but differ in computational approaches and complexity. SVD employs iterative algorithms like Lanczos or power methods to handle any rectangular matrix, typically requiring O(mn^2) operations for an m-by-n matrix, making it computationally intensive for large-scale problems. The Spectral Theorem applies specifically to normal matrices and uses eigenvalue decomposition with complexity O(n^3) for an n-by-n matrix, which can be optimized further for sparse or structured matrices.
Applications in Data Science and Machine Learning
Singular Value Decomposition (SVD) is extensively used in data science for dimensionality reduction, noise reduction, and feature extraction in large datasets, particularly in recommender systems and image compression. The Spectral Theorem provides the foundation for Principal Component Analysis (PCA) by enabling the diagonalization of covariance matrices, facilitating the identification of principal components. Both techniques underpin key machine learning algorithms, enhancing model interpretability, efficiency, and performance in tasks such as clustering, classification, and data visualization.
Advantages and Limitations of Each Approach
Singular Value Decomposition (SVD) provides a robust factorization for any m-by-n matrix, enabling optimal low-rank approximations and applications in noise reduction, data compression, and principal component analysis. The Spectral Theorem applies specifically to normal matrices, ensuring diagonalization via eigenvalues and eigenvectors, which simplifies problems in quantum mechanics and differential equations but limits its scope to symmetric or Hermitian matrices. SVD's advantage lies in its universality across all real and complex matrices, while the Spectral Theorem offers more interpretability and computational efficiency when applicable, yet it cannot handle non-normal matrices.
Connections and Relationships Between SVD and Spectral Theorem
Singular Value Decomposition (SVD) generalizes the Spectral Theorem by decomposing any matrix into orthogonal matrices and a diagonal matrix of singular values, while the Spectral Theorem applies specifically to normal matrices with eigenvalue decomposition. Both methods rely on orthogonal diagonalization tied to eigenvalues or singular values, revealing intrinsic geometric and algebraic structures of matrices. SVD extends the spectral decomposition framework to non-square or non-normal matrices, emphasizing the connection through symmetric matrices like \( A^TA \) or \( AA^T \) whose eigenvalue decompositions underpin singular values.
Conclusion: Choosing the Right Tool
Singular Value Decomposition (SVD) excels in handling any real or complex matrix, delivering optimal low-rank approximations and robust data compression for machine learning and signal processing applications. The Spectral Theorem applies specifically to normal matrices, providing orthonormal eigenvector decompositions crucial for quantum mechanics and vibration analysis. Selecting between SVD and the Spectral Theorem depends on matrix properties and application needs: use SVD for general, non-square matrices and data reduction, while the Spectral Theorem suits symmetric or normal matrices requiring eigendecomposition.
Singular Value Decomposition Infographic
 libterm.com
libterm.com