Epimorphism is a concept in mathematics, particularly in category theory and abstract algebra, describing morphisms that are surjective or "onto" in nature, ensuring every element in the target is mapped from the source. It plays a critical role in understanding structures and transformations within different mathematical systems by preserving essential properties during mapping. Explore the full article to uncover how epimorphisms influence mathematical theory and applications.
Table of Comparison
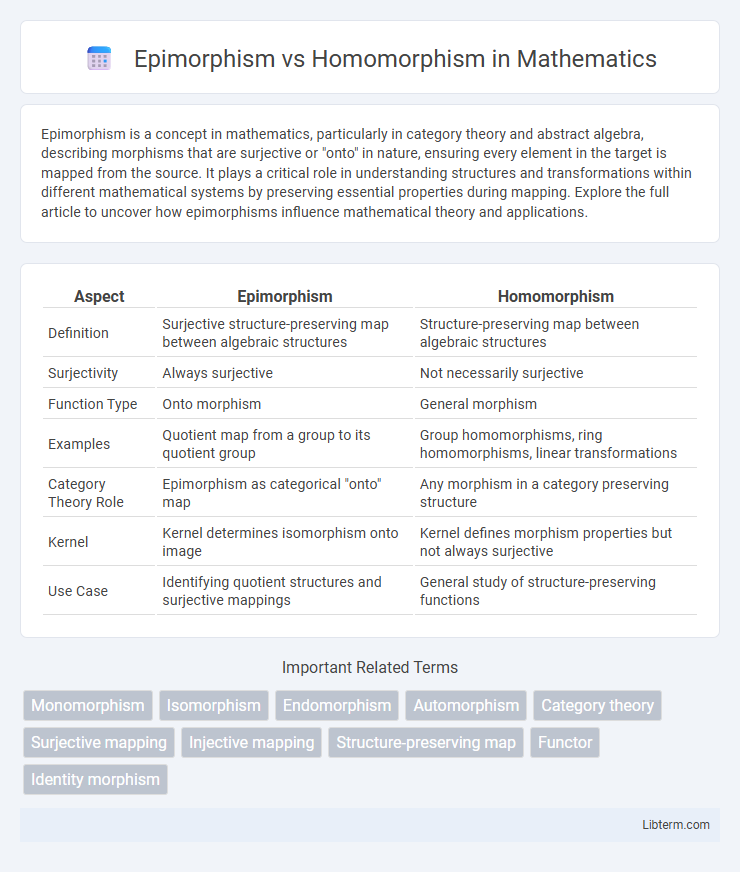
| Aspect | Epimorphism | Homomorphism |
|---|---|---|
| Definition | Surjective structure-preserving map between algebraic structures | Structure-preserving map between algebraic structures |
| Surjectivity | Always surjective | Not necessarily surjective |
| Function Type | Onto morphism | General morphism |
| Examples | Quotient map from a group to its quotient group | Group homomorphisms, ring homomorphisms, linear transformations |
| Category Theory Role | Epimorphism as categorical "onto" map | Any morphism in a category preserving structure |
| Kernel | Kernel determines isomorphism onto image | Kernel defines morphism properties but not always surjective |
| Use Case | Identifying quotient structures and surjective mappings | General study of structure-preserving functions |
Introduction to Morphisms in Algebra
Epimorphisms and homomorphisms are fundamental concepts in abstract algebra, describing structure-preserving maps between algebraic objects such as groups, rings, and vector spaces. A homomorphism is a function that respects the operations of the algebraic structures, ensuring compatibility between their algebraic operations. Epimorphisms are special types of homomorphisms that are surjective, meaning they map onto the entire target structure, playing a key role in quotient structures and algebraic classification.
Understanding Homomorphism
Homomorphism is a fundamental concept in algebra and category theory, describing a structure-preserving map between two algebraic structures such as groups, rings, or vector spaces. It ensures that operations performed within one structure correspond directly to operations in another, preserving the algebraic properties and relations. Understanding homomorphisms is essential for analyzing how different mathematical objects relate and transform while maintaining their inherent structure.
Defining Epimorphism
Epimorphism is a morphism in category theory that is right-cancellable, meaning if two morphisms composed after it are equal, the two morphisms must themselves be equal. This property distinguishes epimorphisms from homomorphisms, where the latter generally preserve algebraic structures such as groups or rings but do not necessarily have the right-cancellability condition. Epimorphisms often serve as categorical analogues to surjective functions, playing a crucial role in defining quotient structures and factorization systems within algebraic and categorical contexts.
Key Differences: Epimorphism vs. Homomorphism
Epimorphism and homomorphism are fundamental concepts in algebra that describe structure-preserving maps between algebraic objects. Homomorphisms are general mappings that maintain operation consistency without requiring surjectivity, while epimorphisms are homomorphisms that are surjective, ensuring every element in the target structure has a preimage. The key difference lies in surjectivity: all epimorphisms are homomorphisms, but not all homomorphisms qualify as epimorphisms.
Examples of Homomorphisms
Homomorphisms are structure-preserving maps between algebraic structures like groups, rings, or vector spaces that respect the operations defining those structures. Classic examples include the group homomorphism from the integers under addition (Z, +) to the integers modulo n (Z/nZ, +), mapping an integer to its remainder mod n, and the ring homomorphism from the polynomial ring R[x] to R given by evaluation at a fixed point. These examples illustrate how homomorphisms maintain algebraic properties and enable the study of complex structures through simpler images.
Illustrative Examples of Epimorphisms
Epimorphisms in algebra are surjective homomorphisms that map one algebraic structure onto another, ensuring every element in the target has a preimage in the source. For example, the canonical projection from the group of integers \(\mathbb{Z}\) onto the cyclic group \(\mathbb{Z}/n\mathbb{Z}\) is an epimorphism, as every element modulo \(n\) is covered. This contrasts with homomorphisms that may not be surjective, such as the inclusion map from a subgroup \(H \subset G\), which is a homomorphism but not necessarily an epimorphism.
Properties of Homomorphism and Epimorphism
Homomorphisms preserve algebraic structure by mapping elements between algebraic objects while maintaining operation consistency, ensuring image closure under these operations. Epimorphisms are surjective homomorphisms, guaranteeing that every element in the codomain has a preimage, thus making the morphism onto. Both types exhibit composition stability and kernel properties, where homomorphisms often have kernels defining congruence relations, and epimorphisms further imply exact sequences in category theory contexts.
Role of Morphisms in Category Theory
Morphisms in category theory serve as the fundamental structure-preserving maps between objects, with epimorphisms representing surjective-like arrows that ensure right-cancellability and homomorphisms embodying general structure-preserving functions without surjectivity requirements. Epimorphisms play a crucial role in defining quotient objects and factorization systems, often indicating surjective mappings in concrete categories, while homomorphisms provide the baseline for morphisms that respect algebraic operations across various categories. Understanding the distinction between epimorphisms and homomorphisms is essential for analyzing object relationships and categorical constructions such as limits, colimits, and image factorization.
Applications in Abstract Algebra
Epimorphisms and homomorphisms are fundamental in abstract algebra for understanding structure-preserving maps between algebraic objects such as groups, rings, and modules. Epimorphisms, being surjective homomorphisms, are crucial in the study of quotient structures and factorization theorems, enabling the construction of isomorphic images and simplifying complex algebraic systems. Homomorphisms provide the framework for morphisms in category theory, facilitating the analysis of algebraic properties through kernel and image, essential for classifying algebraic structures and proving isomorphism theorems.
Summary and Key Takeaways
Epimorphisms and homomorphisms are fundamental concepts in abstract algebra, where homomorphisms are structure-preserving maps between algebraic objects, and epimorphisms are surjective homomorphisms ensuring onto mappings. The key difference lies in epimorphisms requiring surjectivity, which impacts the ability to factor algebraic structures and influences the kernel and image properties. Understanding the distinction aids in categorizing algebraic morphisms and analyzing their effects on algebraic structures like groups, rings, and modules.
Epimorphism Infographic
 libterm.com
libterm.com