The tensor product combines two vector spaces into a new, higher-dimensional space, enabling complex mappings crucial in fields like quantum computing and multilinear algebra. This operation preserves the structures of original spaces while facilitating interactions between their elements. Explore the rest of the article to understand how tensor products can power your advanced mathematical and physical applications.
Table of Comparison
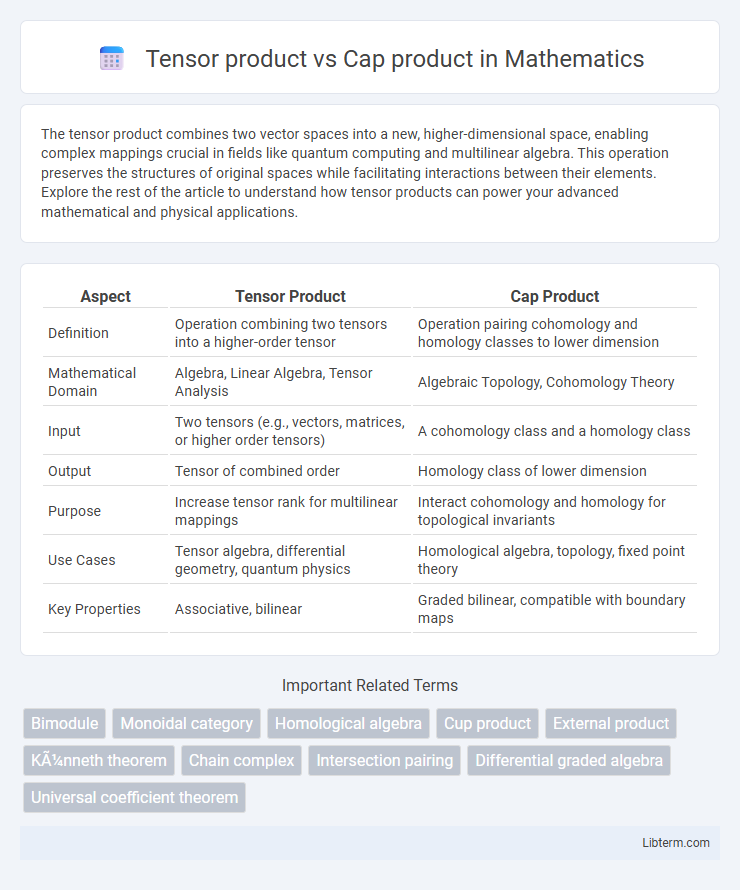
| Aspect | Tensor Product | Cap Product |
|---|---|---|
| Definition | Operation combining two tensors into a higher-order tensor | Operation pairing cohomology and homology classes to lower dimension |
| Mathematical Domain | Algebra, Linear Algebra, Tensor Analysis | Algebraic Topology, Cohomology Theory |
| Input | Two tensors (e.g., vectors, matrices, or higher order tensors) | A cohomology class and a homology class |
| Output | Tensor of combined order | Homology class of lower dimension |
| Purpose | Increase tensor rank for multilinear mappings | Interact cohomology and homology for topological invariants |
| Use Cases | Tensor algebra, differential geometry, quantum physics | Homological algebra, topology, fixed point theory |
| Key Properties | Associative, bilinear | Graded bilinear, compatible with boundary maps |
Introduction to Tensor Product and Cap Product
Tensor product combines two modules or vector spaces to create a new space capturing all bilinear relationships, essential in multilinear algebra and homological algebra. Cap product acts on cohomology and homology groups, linking cohomological operations with geometric intersections in algebraic topology. Understanding these operations facilitates advanced computations in topology, homological algebra, and category theory.
Algebraic Foundations of Tensor Product
The tensor product in algebraic foundations is a bilinear construction that combines modules over a commutative ring, forming a new module capturing multilinear interactions, contrasting the cap product which operates within cohomology and homology theories. Tensor products enable the representation of multilinear maps as linear maps on a combined space, crucial for module theory, category theory, and homological algebra. This algebraic structure facilitates decompositions and exact sequences fundamental to understanding module extensions, while the cap product primarily encodes geometric intersection pairing in topological contexts.
Homological Interpretation of Cap Product
The cap product in algebraic topology is a bilinear operation combining a cohomology class and a homology class, yielding a lower-dimensional homology class that reflects the intersection pairing on a manifold. Its homological interpretation relates to the natural pairing in chain complexes where the cap product acts as a chain-level operation, providing a link between singular cohomology and homology via the evaluation of cochains on chains. In contrast, the tensor product primarily constructs new modules or chain complexes, lacking the direct interpretation of a geometric intersection or evaluation inherent to the cap product's role in Poincare duality.
Mathematical Definitions and Properties
The tensor product of two vector spaces or modules is a bilinear operation that produces a new space encapsulating all bilinear maps from the Cartesian product into another space, characterized by the universal property of bilinearity. The cap product is an algebraic operation in homology and cohomology that combines a cohomology class with a homology class, producing a lower-dimensional homology class, and it respects the grading and module structures over the cohomology ring. While the tensor product focuses on bilinear mappings and constructing new algebraic objects, the cap product provides an interaction between homological and cohomological elements, often used in Poincare duality.
Applications in Algebraic Topology
Tensor products enable the construction of new chain complexes by combining modules, facilitating computations in homology and cohomology theories. Cap products establish an interaction between homology and cohomology classes, providing a powerful tool for Poincare duality and intersection theory on manifolds. These operations play crucial roles in the study of characteristic classes, spectral sequences, and the algebraic structure of topological invariants.
Key Differences: Tensor Product vs Cap Product
The tensor product combines two chain complexes or modules, producing an object that algebraically represents their joint structure, essential in homological algebra for constructing chain complexes on product spaces. The cap product, however, is an operation between a homology class and a cohomology class, yielding a lower-dimensional homology class, pivotal in Poincare duality and intersection theory. While the tensor product focuses on combining algebraic structures, the cap product serves specifically as an action relating homology and cohomology groups.
Examples Illustrating Tensor and Cap Products
Tensor products combine vector spaces or modules by pairing elements from each space to form a new space, commonly illustrated by the space of bilinear forms formed from two vector spaces V and W, where each element can be expressed as a finite sum of tensors v w. Cap products arise in algebraic topology, pairing cohomology and homology classes to produce new homology classes, exemplified by the cap product of a cohomology class in H^k(X; R) with a homology class in H_n(X; R) yielding an element in H_{n-k}(X; R). For instance, in singular homology, using a 1-cochain (a function on edges) and a 2-chain (a formal sum of triangles), the cap product combines these to obtain a 1-chain, demonstrating an intersection-type operation reflecting geometric intuition.
Computational Aspects and Algorithms
Tensor product algorithms focus on efficiently computing multilinear maps and decompositions in high-dimensional vector spaces, often leveraging optimized matrix multiplication techniques to reduce complexity. Cap product computations involve chain-cochain pairings in algebraic topology, requiring specialized algorithms to handle boundary operators and cohomological indexing, with implementations typically optimized for sparse data structures. Advances in computational homology software have integrated both products, utilizing persistent homology frameworks to improve scalability and accuracy in topological data analysis.
Significance in Modern Mathematics
The tensor product serves as a foundational operation in linear algebra and category theory, enabling the construction of complex structures such as multilinear maps and representation of quantum states. The cap product plays a crucial role in algebraic topology by linking cohomology and homology, facilitating computations of intersection pairings and Poincare duality. Together, these products enhance the understanding of algebraic and topological invariants, driving advancements in fields like homological algebra and topological quantum field theory.
Summary and Further Reading
The tensor product combines two algebraic structures into a new, larger structure, often used to study multilinear maps and modules over a ring, while the cap product is a bilinear operation pairing homology and cohomology classes to produce lower-dimensional homology classes, enhancing calculations in algebraic topology. For deeper insights, consult Hatcher's "Algebraic Topology" for cap product applications and Rotman's "An Introduction to Homological Algebra" for tensor product theory. Online lecture notes and articles on homological algebra and algebraic topology provide further examples and proofs to solidify understanding of these products.
Tensor product Infographic
 libterm.com
libterm.com