Nonnegative values play a crucial role in various fields such as mathematics, computer science, and economics, representing quantities that cannot be less than zero. Understanding how to work with nonnegative numbers can improve your problem-solving skills and ensure accurate data interpretation in real-world contexts. Explore the rest of this article to deepen your knowledge on nonnegative concepts and their practical applications.
Table of Comparison
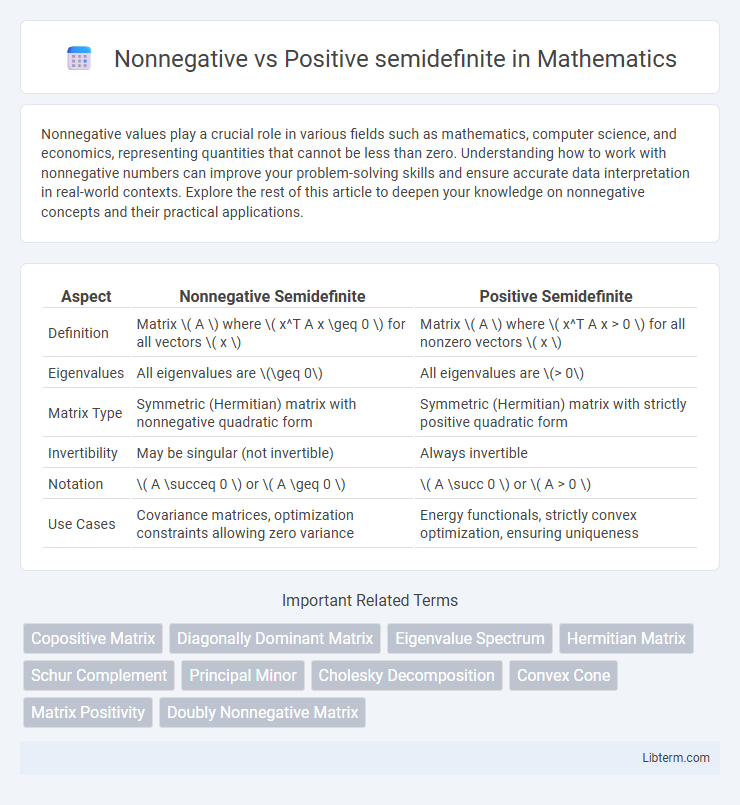
| Aspect | Nonnegative Semidefinite | Positive Semidefinite |
|---|---|---|
| Definition | Matrix \( A \) where \( x^T A x \geq 0 \) for all vectors \( x \) | Matrix \( A \) where \( x^T A x > 0 \) for all nonzero vectors \( x \) |
| Eigenvalues | All eigenvalues are \(\geq 0\) | All eigenvalues are \(> 0\) |
| Matrix Type | Symmetric (Hermitian) matrix with nonnegative quadratic form | Symmetric (Hermitian) matrix with strictly positive quadratic form |
| Invertibility | May be singular (not invertible) | Always invertible |
| Notation | \( A \succeq 0 \) or \( A \geq 0 \) | \( A \succ 0 \) or \( A > 0 \) |
| Use Cases | Covariance matrices, optimization constraints allowing zero variance | Energy functionals, strictly convex optimization, ensuring uniqueness |
Understanding Nonnegative Matrices
Nonnegative matrices consist solely of entries greater than or equal to zero, which ensures that their eigenvalues and principal minors reflect specific stability properties important in systems theory and economics. Positive semidefinite matrices are a subset of symmetric matrices where all eigenvalues are nonnegative, guaranteeing nonnegative quadratic forms and serving as a fundamental concept in optimization and statistics. Understanding nonnegative matrices involves analyzing their spectral radius and irreducibility, which deeply influence convergence behavior and matrix decompositions used in applied mathematics.
Defining Positive Semidefinite Matrices
Positive semidefinite matrices are defined as symmetric matrices whose eigenvalues are all nonnegative, ensuring that for any nonzero vector \(x\), the quadratic form \(x^T A x \geq 0\). Nonnegative semidefinite is often used interchangeably with positive semidefinite, emphasizing the eigenvalue spectrum's nonnegativity rather than strict positivity. This property guarantees that the matrix represents a convex function or a valid covariance matrix in statistics and optimization contexts.
Key Differences Between Nonnegative and Positive Semidefinite
Nonnegative semidefinite matrices have all eigenvalues greater than or equal to zero, ensuring they never produce negative quadratic forms, while positive semidefinite matrices strictly require all eigenvalues to be strictly positive except possibly zero eigenvalues corresponding to singular matrices. Nonnegative semidefinite matrices include positive semidefinite ones but also allow for null eigenvalues that may reduce matrix rank, impacting solutions in optimization and machine learning. In contrast, positive semidefinite matrices guarantee non-negative definiteness with stronger properties that support stability and convergence in numerical methods.
Mathematical Properties of Nonnegative Matrices
Nonnegative matrices possess entries that are zero or positive, influencing their spectral properties with the Perron-Frobenius theorem guaranteeing a real nonnegative eigenvalue equal to the spectral radius. Positive semidefinite matrices, defined by symmetric matrices with all nonnegative eigenvalues, ensure quadratic forms are nonnegative and arise frequently in optimization and covariance analysis. The mathematical distinction lies in nonnegative matrices emphasizing entry-wise constraints, while positive semidefinite matrices focus on eigenvalue positivity and symmetry conditions.
Spectral Characteristics of Positive Semidefinite Matrices
Positive semidefinite matrices exhibit nonnegative eigenvalues, reflecting their spectral properties, whereas nonnegative matrices have all elements greater or equal to zero but may have negative eigenvalues. The spectral characteristics of positive semidefinite matrices ensure all eigenvalues are real and nonnegative, enabling stable quadratic forms and guaranteeing matrix decompositions like Cholesky. This distinction is critical in optimization, statistics, and numerical analysis, where the spectral behavior influences matrix definiteness and associated algorithmic stability.
Applications in Linear Algebra and Data Science
Nonnegative semidefinite matrices, characterized by all nonnegative eigenvalues, are fundamental in covariance matrix estimation and kernel methods for machine learning, ensuring data variance and similarity measures remain valid. Positive semidefinite matrices, with strictly positive eigenvalues, guarantee invertibility and stability in optimization problems, such as quadratic programming and regularization techniques in data science. Both matrix classes underpin principal component analysis (PCA) and support vector machines (SVMs), where the spectral properties directly influence model performance and interpretability.
Visualization of Nonnegative vs Positive Semidefinite
Visualizing nonnegative matrices typically involves examining elements that are all zero or positive, representing constraints in linear programming or probability distributions, while positive semidefinite (PSD) matrices relate to quadratic forms and can be visualized as ellipsoids or convex cones in multidimensional space. Heatmaps or color gradients often illustrate nonnegative matrices by highlighting zero or positive entries, whereas PSD matrices visualization uses eigenvalue decompositions to show positive eigenvalues ensuring convexity. Graphical representation of PSD matrices emphasizes their role in optimization and stability analysis, contrasting with the element-wise nonnegativity focus in simpler matrix visualizations.
Testing for Nonnegativity and Positive Semidefiniteness
Testing for nonnegativity involves verifying that a function or matrix output is never negative for all inputs within a specified domain, often requiring sum-of-squares decompositions or interval evaluations. Positive semidefiniteness testing of matrices uses eigenvalue analysis or Cholesky decomposition to confirm all eigenvalues are nonnegative, ensuring the matrix represents a valid covariance or Gram matrix. Efficient algorithms leverage semidefinite programming to certify these properties, essential in optimization, control theory, and machine learning.
Common Misconceptions and Confusions
Nonnegative semidefinite matrices are often mistakenly assumed to be strictly positive semidefinite, but the key difference lies in their eigenvalues: nonnegative semidefinite matrices allow zero eigenvalues, whereas positive semidefinite matrices require all eigenvalues to be strictly positive. A common confusion arises in optimization problems where nonnegative semidefiniteness is used as a constraint, yet is incorrectly interpreted as positive definiteness, which affects solution feasibility and stability. Clarifying this distinction is crucial in fields like machine learning and control theory, where matrix definiteness impacts algorithm performance and system robustness.
Summary and Practical Implications
Nonnegative semidefinite matrices have all eigenvalues greater than or equal to zero, ensuring nonnegative quadratic forms, while positive semidefinite matrices require all eigenvalues strictly greater than zero, guaranteeing positive quadratic forms except at the zero vector. In practical terms, nonnegative semidefinite matrices are essential in optimization problems and statistical models for ensuring convexity and stability, whereas positive semidefinite matrices provide stronger guarantees for invertibility and uniqueness in solutions. Understanding the distinction influences algorithm design in machine learning and control systems, where matrix properties directly affect performance and convergence criteria.
Nonnegative Infographic
 libterm.com
libterm.com