Soundness refers to the quality of being logically valid and well-founded, ensuring that arguments or systems are free from errors or inconsistencies. In fields like mathematics, logic, and engineering, soundness guarantees reliable outcomes based on accurate premises or components. Explore the article to understand how soundness applies to your specific area of interest and why it is essential for trustworthiness.
Table of Comparison
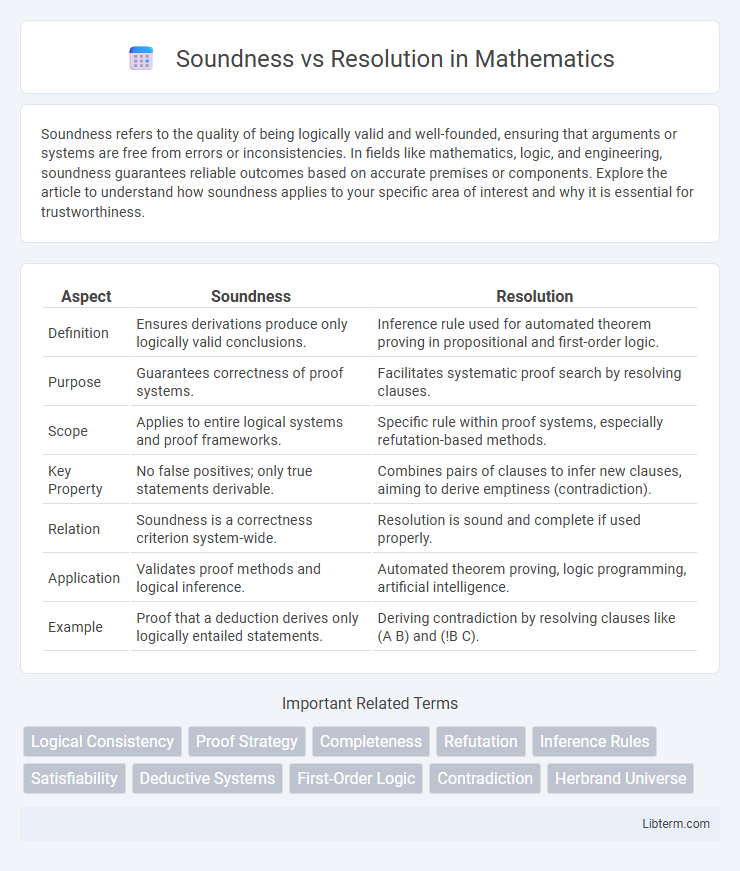
| Aspect | Soundness | Resolution |
|---|---|---|
| Definition | Ensures derivations produce only logically valid conclusions. | Inference rule used for automated theorem proving in propositional and first-order logic. |
| Purpose | Guarantees correctness of proof systems. | Facilitates systematic proof search by resolving clauses. |
| Scope | Applies to entire logical systems and proof frameworks. | Specific rule within proof systems, especially refutation-based methods. |
| Key Property | No false positives; only true statements derivable. | Combines pairs of clauses to infer new clauses, aiming to derive emptiness (contradiction). |
| Relation | Soundness is a correctness criterion system-wide. | Resolution is sound and complete if used properly. |
| Application | Validates proof methods and logical inference. | Automated theorem proving, logic programming, artificial intelligence. |
| Example | Proof that a deduction derives only logically entailed statements. | Deriving contradiction by resolving clauses like (A B) and (!B C). |
Introduction to Soundness and Resolution
Soundness in logic ensures that any conclusion derived from a set of premises is semantically valid, meaning that the inference rules produce only true statements when applied to true premises. Resolution is a rule of inference used in automated theorem proving, particularly in propositional and first-order logic, which systematically applies refutation by contradiction to derive a contradiction from the negation of a goal. Understanding the soundness of resolution guarantees that any proof obtained through resolution is logically valid and corresponds to a true logical consequence of the original premises.
Defining Soundness in Logic
Soundness in logic ensures that any statement derived through a proof system is semantically valid, meaning if the system proves a formula, that formula must be true in all interpretations or models. This property guarantees that no false conclusions can be inferred from true premises within the logical framework. In contrast to resolution, which is a specific proof technique, soundness serves as a fundamental correctness criterion for inference rules applied in logic systems.
Understanding Resolution in Proof Systems
Resolution in proof systems is a rule of inference primarily used in automated theorem proving and propositional logic, enabling the derivation of contradictions through systematic clause combination. This method guarantees soundness by producing only conclusions that logically follow from the given premises, ensuring no false statements are derived. Understanding resolution involves recognizing its role in refutation proofs where it simplifies complex logical formulas into an unsatisfiable set, streamlining the proof verification process.
Key Differences: Soundness vs Resolution
Soundness ensures that every statement derived by a logical system is true in all interpretations where the premises are true, guaranteeing no false conclusions. Resolution is a specific inference rule used in automated theorem proving that systematically combines clauses to derive a contradiction or prove unsatisfiability. The key difference lies in soundness being a property of the entire inference system's reliability, while resolution is a concrete proof technique within that system.
Importance of Soundness in Logical Reasoning
Soundness in logical reasoning guarantees that any derived conclusion is both valid and true within the system, ensuring reliability in proof systems. Unlike resolution, which is a rule of inference mainly used for automated theorem proving, soundness ensures that no false statements can be inferred from true premises. This importance makes soundness a fundamental criterion for assessing the trustworthiness of formal logical arguments and computational logic algorithms.
The Role of Resolution in Automated Theorem Proving
Resolution serves as a fundamental inference rule in automated theorem proving, enabling the systematic derivation of conclusions from given premises. Its soundness guarantees that any formula derived through resolution-based procedures is logically entailed by the original set of clauses. By iteratively applying resolution, automated theorem provers efficiently explore the search space to detect contradictions, thereby confirming the validity of theorems within propositional and first-order logic frameworks.
Common Applications of Soundness and Resolution
Soundness ensures that any derived conclusion in formal systems, such as logic programming and automated theorem proving, is logically valid and trustworthy, which is critical in software verification and database query optimization. Resolution, a rule of inference primarily used in automated reasoning and artificial intelligence, enables efficient proof searches by refuting contradictions, commonly applied in knowledge representation and expert systems. Combining soundness with resolution guarantees that the inference engine produces only correct results while efficiently handling complex logical formulas in applications like model checking and natural language processing.
Limitations of Soundness and Resolution Techniques
Soundness ensures that all derived conclusions are logically valid, but it cannot guarantee completeness, often missing valid inferences in complex knowledge bases. Resolution techniques, while powerful for automated theorem proving, struggle with inefficiency and combinatorial explosion in large or intricate datasets. Both approaches face limitations in handling uncertainty and real-world ambiguity, restricting their effectiveness in practical reasoning applications.
Real-World Examples: Soundness vs Resolution
In legal systems, soundness ensures that every derived conclusion is logically valid based on premises, preventing wrongful convictions through flawed reasoning. Resolution, as a rule of inference in automated theorem proving, efficiently combines clauses to derive contradictions, speeding up proof discovery in complex cases like patent disputes. In fault detection for electrical circuits, soundness guarantees only actual faults trigger alarms, while resolution algorithms help deduce fault locations rapidly from sensor data, improving diagnosis accuracy and response time.
Conclusion: Choosing Between Soundness and Resolution
Choosing between soundness and resolution depends on the specific goals of the reasoning system; soundness ensures that all derived conclusions are logically valid, preventing false positives, while resolution guarantees completeness, enabling the derivation of all logical consequences from a given knowledge base. In applications requiring absolute reliability, such as formal verification, soundness is prioritized to maintain consistency and trustworthiness. Conversely, in automated theorem proving and logic programming, resolution is preferred for its ability to derive all possible conclusions, even if it risks generating some unsupported results.
Soundness Infographic
 libterm.com
libterm.com