The Fourier transform is a mathematical operation that decomposes a function or signal into its constituent frequencies, revealing the frequency spectrum hidden within complex data. This powerful tool is widely used in signal processing, communications, and image analysis to analyze temporal or spatial variations efficiently. Explore the rest of the article to understand how the Fourier transform can enhance your data analysis techniques.
Table of Comparison
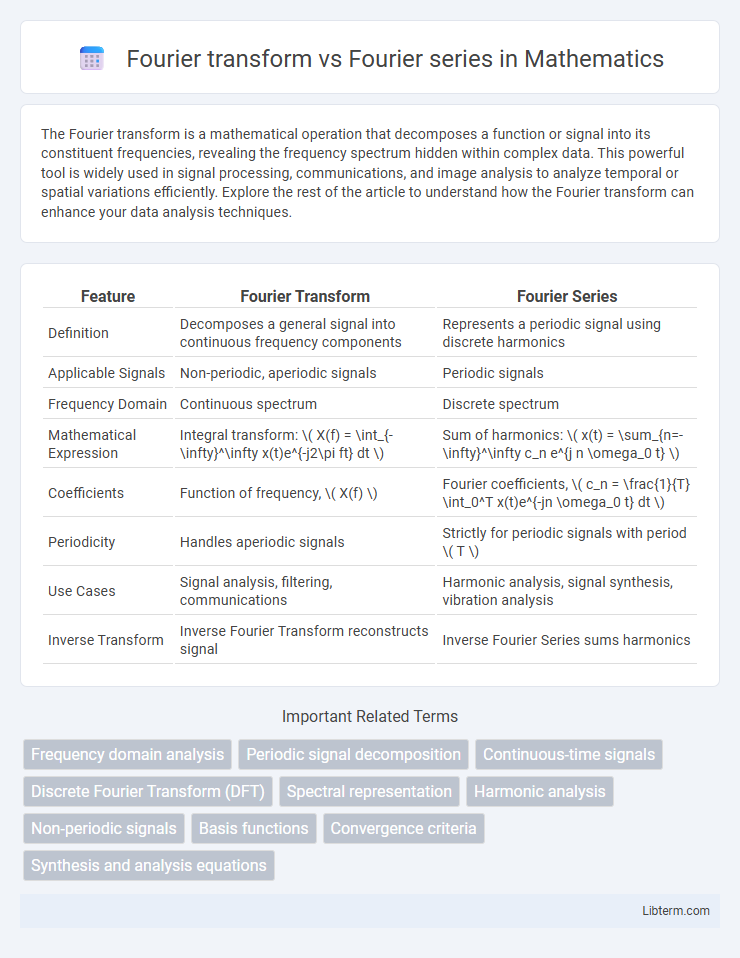
| Feature | Fourier Transform | Fourier Series |
|---|---|---|
| Definition | Decomposes a general signal into continuous frequency components | Represents a periodic signal using discrete harmonics |
| Applicable Signals | Non-periodic, aperiodic signals | Periodic signals |
| Frequency Domain | Continuous spectrum | Discrete spectrum |
| Mathematical Expression | Integral transform: \( X(f) = \int_{-\infty}^\infty x(t)e^{-j2\pi ft} dt \) | Sum of harmonics: \( x(t) = \sum_{n=-\infty}^\infty c_n e^{j n \omega_0 t} \) |
| Coefficients | Function of frequency, \( X(f) \) | Fourier coefficients, \( c_n = \frac{1}{T} \int_0^T x(t)e^{-jn \omega_0 t} dt \) |
| Periodicity | Handles aperiodic signals | Strictly for periodic signals with period \( T \) |
| Use Cases | Signal analysis, filtering, communications | Harmonic analysis, signal synthesis, vibration analysis |
| Inverse Transform | Inverse Fourier Transform reconstructs signal | Inverse Fourier Series sums harmonics |
Introduction to Fourier Transform and Fourier Series
Fourier series decompose periodic functions into sums of sines and cosines, ideal for analyzing signals with repeating patterns. Fourier transform extends this concept to non-periodic signals by converting time-domain data into continuous frequency spectra, enabling comprehensive frequency analysis of any signal. Both tools are fundamental in signal processing, with Fourier series focusing on discrete frequency components and Fourier transform addressing continuous frequency distributions.
Fundamental Concepts and Definitions
The Fourier transform decomposes a continuous-time signal into its constituent frequencies, providing a spectrum of sinusoidal components over a continuous frequency range, while the Fourier series represents a periodic signal as a sum of discrete sinusoidal harmonics at integer multiples of a fundamental frequency. Fourier series rely on the concept of periodicity and the orthogonality of sine and cosine functions over one period, enabling the reconstruction of the signal from its harmonic coefficients. The Fourier transform extends these principles to non-periodic signals by integrating over all time, yielding a continuous frequency spectrum that generalizes the discrete frequency components of the Fourier series.
Mathematical Formulations
Fourier series decomposes a periodic function into an infinite sum of sines and cosines with discrete frequencies expressed as integer multiples of the fundamental frequency, mathematically represented as \( f(t) = \sum_{n=-\infty}^{\infty} c_n e^{i n \omega_0 t} \) where \( c_n \) are Fourier coefficients and \( \omega_0 \) is the fundamental angular frequency. The Fourier transform generalizes this concept for non-periodic functions by representing them as integrals over continuous frequency spectra, written as \( F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt \), allowing analysis in the frequency domain without periodicity constraints. Both formulations rely on orthogonal basis functions in the complex exponential form \( e^{i \omega t} \), but Fourier series applies to discrete frequencies due to periodicity, while Fourier transform integrates over all real frequencies.
Application Domains
Fourier transform excels in analyzing non-periodic signals and continuous spectra, making it essential in fields like signal processing, telecommunications, and quantum physics. Fourier series are primarily used for representing periodic functions, widely applied in electrical engineering, acoustics, and vibration analysis. Both techniques enable frequency domain analysis but differ crucially in their suitability for discrete versus continuous, periodic versus aperiodic signals.
Periodic vs Aperiodic Signals
Fourier series decomposes periodic signals into a sum of sinusoids with discrete frequencies, capturing the signal's fundamental period and its harmonics. Fourier transform generalizes this concept by analyzing aperiodic signals, producing a continuous spectrum that represents all possible frequency components. Periodic signals have spectra with distinct impulses, while aperiodic signals exhibit continuous frequency distributions in their Fourier transform.
Computational Aspects
Fourier transform facilitates analysis of non-periodic signals by converting them into continuous frequency spectra, while Fourier series decomposes periodic signals into discrete sums of harmonics. Computationally, Fourier transform leverages algorithms like the Fast Fourier Transform (FFT) for efficient computation of large datasets, enabling real-time signal processing. Fourier series require evaluation of coefficients through integration or summation over one period, which can be computationally intensive for complex waveforms compared to FFT-based transforms.
Strengths and Limitations
Fourier transform excels in analyzing continuous, non-periodic signals by converting them into frequency spectra, making it ideal for real-world signal processing and image analysis, while its limitation lies in assuming infinite signal duration and potentially producing complex spectra. Fourier series effectively represents periodic signals by decomposing them into discrete harmonics, providing clear frequency components useful in vibration analysis and acoustics, but it is limited to periodic functions and cannot directly handle non-periodic signals. Both methods complement each other, with Fourier series offering a discrete frequency approach and Fourier transform providing a continuous frequency representation.
Real-World Examples
Fourier series decomposes periodic signals like musical notes or electrical AC waveforms into their fundamental frequencies, enabling analysis and synthesis in sound engineering and power distribution. Fourier transform applies to non-periodic signals, crucial for processing real-world data such as seismic vibrations in geophysics or MRI scans in medical imaging. The transform's ability to provide frequency spectrum insight makes it indispensable for telecommunications, radar, and speech recognition technologies.
Key Differences Summarized
Fourier transform converts a time-domain signal into a continuous frequency spectrum, ideal for non-periodic and aperiodic signals, while Fourier series represents a periodic signal as a sum of discrete sinusoidal components. Fourier transform deals with integrals over infinite intervals, providing a continuous frequency representation, whereas Fourier series uses discrete sums over one period of the signal. Key differences include the Fourier transform's application to infinite or non-periodic functions versus the Fourier series' limitation to periodic functions and its discrete frequency spectrum output.
Conclusion and Further Reading
Fourier transform extends the Fourier series by representing non-periodic signals through continuous frequency spectra, enabling analysis of a wider class of signals beyond periodic ones. Fourier series decomposes periodic signals into discrete harmonics, making it suitable for steady-state signal analysis with clear fundamental frequencies. For further reading, explore texts like "The Fourier Transform and Its Applications" by Bracewell and "Signals and Systems" by Oppenheim for in-depth treatment of both tools in practical signal analysis contexts.
Fourier transform Infographic
 libterm.com
libterm.com