Lebesgue measure is a fundamental concept in real analysis and measure theory, providing a way to assign a consistent "size" or "volume" to subsets of n-dimensional space. Unlike simpler measures, it accurately handles complex and irregular sets, playing a crucial role in integration and probability theory. Dive into the rest of the article to deepen your understanding of Lebesgue measure and its applications.
Table of Comparison
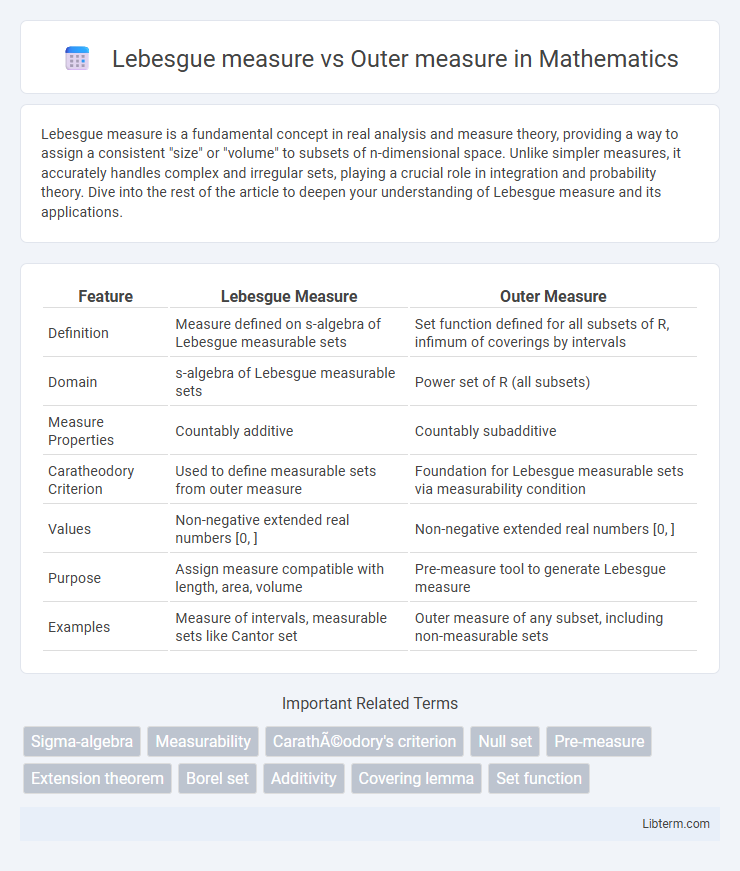
| Feature | Lebesgue Measure | Outer Measure |
|---|---|---|
| Definition | Measure defined on s-algebra of Lebesgue measurable sets | Set function defined for all subsets of R, infimum of coverings by intervals |
| Domain | s-algebra of Lebesgue measurable sets | Power set of R (all subsets) |
| Measure Properties | Countably additive | Countably subadditive |
| Caratheodory Criterion | Used to define measurable sets from outer measure | Foundation for Lebesgue measurable sets via measurability condition |
| Values | Non-negative extended real numbers [0, ] | Non-negative extended real numbers [0, ] |
| Purpose | Assign measure compatible with length, area, volume | Pre-measure tool to generate Lebesgue measure |
| Examples | Measure of intervals, measurable sets like Cantor set | Outer measure of any subset, including non-measurable sets |
Introduction to Measure Theory
Lebesgue measure extends outer measure by assigning a consistent volume to a broader class of sets, crucial in measure theory for integrating complex functions. Outer measure, a preliminary tool, defines a set's size using countable coverings by intervals, enabling the construction of Lebesgue measurable sets. This distinction allows Lebesgue measure to handle sets with intricate structures that outer measure alone cannot adequately quantify.
Defining Outer Measure
Defining outer measure involves assigning a non-negative extended real number to any subset of a given space, typically constructed as the infimum of the sums of volumes of countable collections of intervals covering the set. This approach gives a preliminary tool to quantify "size" without requiring the set to be measurable, unlike Lebesgue measure, which refines outer measure by restricting to measurable sets satisfying Caratheodory's criterion. Outer measure serves as a foundational step for Lebesgue measure, enabling a consistent extension of length, area, and volume concepts beyond simple geometric shapes.
Understanding Lebesgue Measure
Lebesgue measure is a fundamental concept in real analysis that assigns a non-negative size or volume to subsets of Euclidean space, extending the notion of length, area, and volume beyond simple geometric figures. Unlike outer measure, which provides an initial assignment of size by covering sets with intervals and taking the infimum of their total length, Lebesgue measure is defined for a broader class of sets called Lebesgue measurable sets, ensuring countable additivity and compatibility with limit operations. Understanding Lebesgue measure involves grasping its construction via Caratheodory's criterion, which selects measurable sets from those approximated well by intervals in terms of outer measure, thus establishing a rigorous and consistent measure theory framework.
Key Differences Between Outer Measure and Lebesgue Measure
Outer measure assigns a non-negative extended real value to all subsets of a given set, serving as an initial step in measure theory construction, whereas Lebesgue measure is a complete measure defined on the s-algebra of Lebesgue measurable sets that extends the outer measure. Outer measure is countably subadditive but not necessarily additive, while Lebesgue measure is countably additive, ensuring that the measure of disjoint unions equals the sum of their measures. Key differences include the domain of definition, where outer measure applies to all subsets regardless of measurability, and Lebesgue measure requires measurability, guaranteeing stronger structural properties like completeness and translation invariance.
Measurability: Criteria and Implications
Lebesgue measure defines measurability through Caratheodory's criterion, ensuring any set E satisfies m*(A) = m*(A E) + m*(A E^c) for all subsets A, where m* is the outer measure, guaranteeing additivity and completeness. Outer measure, while extending length to arbitrary sets, lacks inherent sigma-additivity and measurability without this criterion, highlighting that only subsets meeting Caratheodory's condition qualify as Lebesgue measurable. This distinction impacts integration theory and measure extension, as Lebesgue measurability ensures consistency and applicability in real analysis and probability.
Construction of the Lebesgue Measure from Outer Measure
The construction of the Lebesgue measure begins with the definition of the Lebesgue outer measure, a set function defined for all subsets of the real line as the infimum of the sums of lengths of open intervals covering the set. Measurable sets are then characterized using Caratheodory's criterion, requiring that for any set A, the outer measure of any other set E equals the sum of the outer measures of E intersected with A and E minus A. This process filters the collection of measurable sets from all subsets, enabling the restriction of the outer measure to the s-algebra of measurable sets, hence defining the complete Lebesgue measure.
Properties of Lebesgue and Outer Measures
Lebesgue measure is a complete measure defined on the s-algebra of Lebesgue measurable sets, ensuring countable additivity and translation invariance, while outer measure is an extended real-valued function defined on all subsets of a given space, satisfying monotonicity and countable subadditivity but lacking countable additivity. Lebesgue measure refines outer measure by restricting to measurable sets where the measure of any set equals the outer measure, guaranteeing measurability and completeness. Outer measure serves as a foundational tool, providing an outer approximation for sets, whereas Lebesgue measure assigns consistent and well-defined sizes to measurable sets under the framework of measure theory.
Examples Illustrating Both Measures
The Lebesgue measure assigns precise sizes to sets like intervals [0,1], ensuring countable additivity and completeness, while outer measure provides an initial, more general way to approximate the size of any subset using coverings by intervals. For example, the Lebesgue measure of the Cantor set is zero despite its uncountable nature, whereas outer measure first uses coverings to define this property before Lebesgue measurability is established. Outer measure may assign a non-zero value to complicated sets by taking the infimum of covering interval lengths, while Lebesgue measure refines this through measurable sets and s-algebras.
Applications in Real Analysis
Lebesgue measure provides a complete and translation-invariant way to assign sizes to subsets of real numbers, enabling integration over complex sets and supporting the development of Lebesgue integral theory in real analysis. Outer measure, defined as the infimum of the sums of lengths of intervals covering a set, serves as a foundational tool to construct Lebesgue measure but lacks countable additivity on all subsets, limiting its direct application in integration. These measures are essential in differentiating measurable sets from non-measurable ones, impacting convergence theorems, measure-theoretic probability, and functional analysis within real analysis.
Summary and Comparative Insights
Lebesgue measure extends outer measure by refining the measurability criterion using Caratheodory's condition, ensuring countable additivity and completeness on measurable sets. Outer measure serves as a preliminary function assigning non-negative values to all subsets but lacks countable additivity and may assign non-measurable sets ambiguous values. The key comparison highlights Lebesgue measure's role in providing a rigorous framework for integration and measurable functions, whereas outer measure functions as a foundational tool in defining measurability and measure extension.
Lebesgue measure Infographic
 libterm.com
libterm.com