Commutative property in mathematics refers to the ability to change the order of numbers in addition or multiplication without affecting the result. This fundamental concept simplifies calculations and ensures consistent outcomes in various algebraic operations. Discover how understanding the commutative property can enhance your problem-solving skills in the rest of the article.
Table of Comparison
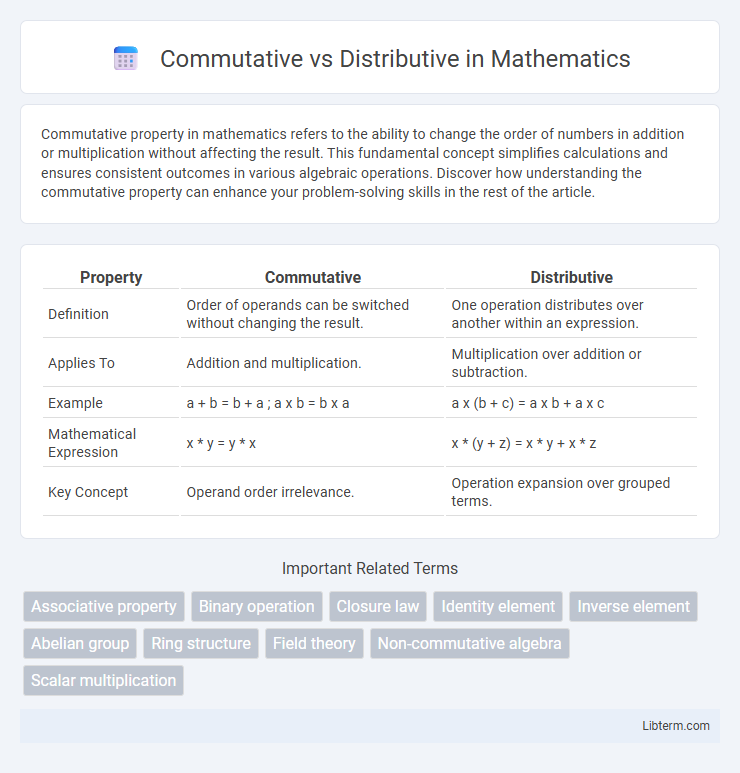
| Property | Commutative | Distributive |
|---|---|---|
| Definition | Order of operands can be switched without changing the result. | One operation distributes over another within an expression. |
| Applies To | Addition and multiplication. | Multiplication over addition or subtraction. |
| Example | a + b = b + a ; a x b = b x a | a x (b + c) = a x b + a x c |
| Mathematical Expression | x * y = y * x | x * (y + z) = x * y + x * z |
| Key Concept | Operand order irrelevance. | Operation expansion over grouped terms. |
Introduction to Commutative and Distributive Properties
The commutative property highlights that changing the order of numbers in addition or multiplication does not affect the result, such as 3 + 5 = 5 + 3 or 4 x 7 = 7 x 4. The distributive property involves multiplying a single term by a sum or difference inside parentheses, demonstrated by a x (b + c) = a x b + a x c. Both properties are fundamental in algebra, enabling simplification and flexibility in solving equations.
Definition of the Commutative Property
The commutative property states that changing the order of numbers in an operation does not affect the result, typically applied to addition and multiplication (e.g., a + b = b + a or a x b = b x a). This property contrasts with the distributive property, which involves multiplying a number by a group of numbers added together, expressed as a(b + c) = ab + ac. Understanding the commutative property is fundamental in algebra and arithmetic for simplifying expressions and solving equations efficiently.
Definition of the Distributive Property
The distributive property defines how multiplication interacts with addition or subtraction within parentheses, stating a(b + c) equals ab + ac. This property allows one to multiply each term inside the parentheses individually before performing the addition or subtraction. It contrasts with the commutative property, which involves the order of numbers in addition or multiplication but does not distribute operations across terms.
Key Differences Between Commutative and Distributive Laws
The commutative law states that the order of numbers does not affect the sum or product, as in a + b = b + a and ab = ba, highlighting its focus on rearranging terms. The distributive law combines both addition and multiplication, showing that a(b + c) = ab + ac, emphasizing the multiplication of a single term across terms inside parentheses. The key difference lies in the commutative law's concern with operand order, while the distributive law addresses the interaction between multiplication and addition within expressions.
Examples of Commutative Property in Mathematics
The commutative property in mathematics states that changing the order of numbers in addition or multiplication does not affect the result, such as 3 + 5 = 5 + 3 or 4 x 7 = 7 x 4. This property applies to addition (a + b = b + a) and multiplication (a x b = b x a) but not to subtraction or division. Examples include 8 + 2 = 2 + 8 and 6 x 9 = 9 x 6, demonstrating the flexibility of number arrangements without altering the outcome.
Examples of Distributive Property in Mathematics
The distributive property in mathematics is illustrated by expressions like a(b + c) = ab + ac, demonstrating how multiplication distributes over addition. For example, 3(4 + 5) equals 3x4 + 3x5, which is 12 + 15, totaling 27. This property is essential for simplifying algebraic expressions and solving equations efficiently.
Real-life Applications of Commutative Property
The commutative property, stating that a + b = b + a or ab = ba, is essential in real-life scenarios such as budgeting, where expenses can be added in any order without affecting the total. In cooking, measurements can be combined interchangeably, reflecting the property's flexibility in preparing recipes. Retail transactions also rely on this concept, allowing prices and quantities to be multiplied or summed regardless of order to calculate totals efficiently.
Real-life Applications of Distributive Property
The distributive property is essential in financial calculations, such as determining total costs when purchasing multiple items with the same price, by breaking down complex expressions into simpler sums. It also plays a pivotal role in algebraic problem-solving, allowing for efficient manipulation of equations in engineering and computer science. Construction and architecture professionals use the distributive property to calculate material requirements by distributing dimensions across quantities for accurate resource estimation.
Common Mistakes and Misconceptions
Common mistakes in understanding the commutative and distributive properties include assuming commutativity applies to subtraction and division, which it does not. Another frequent misconception is confusing the distributive property with simple multiplication, leading to errors when distributing over addition or subtraction inside parentheses. Misapplying these properties can result in incorrect simplification of algebraic expressions and arithmetic calculations.
Summary and Conclusion
The commutative property states that changing the order of numbers in addition or multiplication does not affect the result, as in a + b = b + a or ab = ba. The distributive property connects multiplication and addition by allowing a number to be multiplied by each addend inside parentheses, expressed as a(b + c) = ab + ac. Understanding these properties simplifies algebraic expressions and enhances problem-solving efficiency in mathematics.
Commutative Infographic
 libterm.com
libterm.com