Holder continuity describes a function's behavior where differences in output are bounded by a constant multiplied by a power of the input difference, ensuring smooth and predictable variation. This property is crucial in various fields like partial differential equations, fractal geometry, and numerical analysis for controlling irregularities and ensuring stability. Explore the rest of the article to understand how Holder continuity impacts mathematical modeling and practical applications.
Table of Comparison
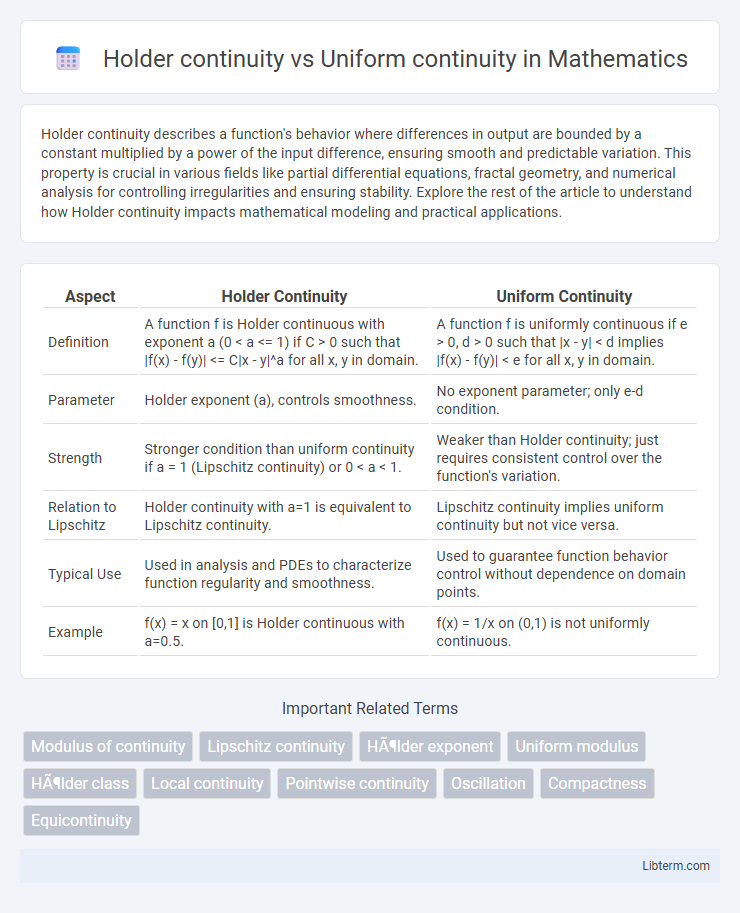
| Aspect | Holder Continuity | Uniform Continuity |
|---|---|---|
| Definition | A function f is Holder continuous with exponent a (0 < a <= 1) if C > 0 such that |f(x) - f(y)| <= C|x - y|^a for all x, y in domain. | A function f is uniformly continuous if e > 0, d > 0 such that |x - y| < d implies |f(x) - f(y)| < e for all x, y in domain. |
| Parameter | Holder exponent (a), controls smoothness. | No exponent parameter; only e-d condition. |
| Strength | Stronger condition than uniform continuity if a = 1 (Lipschitz continuity) or 0 < a < 1. | Weaker than Holder continuity; just requires consistent control over the function's variation. |
| Relation to Lipschitz | Holder continuity with a=1 is equivalent to Lipschitz continuity. | Lipschitz continuity implies uniform continuity but not vice versa. |
| Typical Use | Used in analysis and PDEs to characterize function regularity and smoothness. | Used to guarantee function behavior control without dependence on domain points. |
| Example | f(x) = x on [0,1] is Holder continuous with a=0.5. | f(x) = 1/x on (0,1) is not uniformly continuous. |
Introduction to Continuity in Mathematics
Holder continuity and uniform continuity are key concepts in the study of functions within mathematical analysis, highlighting different degrees of control over function behavior. Holder continuity generalizes uniform continuity by introducing a condition involving a fixed exponent a (0 < a <= 1), with functions satisfying |f(x) - f(y)| <= C|x - y|^a, where C is a constant, ensuring a more stringent smoothness criterion than uniform continuity. Uniform continuity requires that for every e > 0, there exists a d > 0 such that for all x, y in the domain, if |x - y| < d, then |f(x) - f(y)| < e, providing a uniform bound on function variation independent of specific points.
What is Hölder Continuity?
Holder continuity is a condition describing the regularity of functions based on a fixed exponent a (0 < a <= 1), quantifying how a function's values change relative to the distance between points raised to the power a. It generalizes uniform continuity by allowing more precise control of the function's oscillation at smaller scales, often expressed as |f(x) - f(y)| <= C |x - y|^a for some constant C. Functions that satisfy Holder continuity with a = 1 are Lipschitz continuous, indicating a tighter bounded rate of change than uniform continuity alone.
Understanding Uniform Continuity
Uniform continuity ensures that for every e > 0, there is a single d > 0 applicable throughout the entire domain to keep function values within e whenever inputs differ by less than d. This property stronger than ordinary continuity guarantees consistent control over function behavior regardless of location in the domain, making it crucial in analyzing functions on closed intervals. Holder continuity generalizes this by allowing the difference in function values to be bounded by a constant times the input difference raised to a fixed exponent, offering flexibility in measuring smoothness but lacking the uniform d dependency present in uniform continuity.
Mathematical Definitions: Hölder vs Uniform Continuity
Holder continuity defines a function \( f \) as Holder continuous with exponent \( \alpha \in (0,1] \) if there exists a constant \( C > 0 \) such that for all \( x, y \), \( |f(x) - f(y)| \leq C |x - y|^\alpha \); uniform continuity requires for every \( \varepsilon > 0 \), a \( \delta > 0 \) exists where \( |x - y| < \delta \) implies \( |f(x) - f(y)| < \varepsilon \) for all \( x, y \). Holder continuity imposes a stronger, quantitative smoothness condition, controlling how rapidly function values can change relative to distance, while uniform continuity guarantees consistent behavior across the domain without specifying rates. Functions satisfying Holder continuity with \(\alpha=1\) are Lipschitz continuous, a strict subset of uniformly continuous functions, highlighting Holder's parameterized refinement of continuity classes.
Key Similarities Between Hölder and Uniform Continuity
Holder continuity and uniform continuity both describe types of functions where the rate of change is controlled and predictable across the entire domain. Each concept ensures that for any two points in the domain, the difference in function values can be bounded by a function of the distance between these points, promoting stability in function behavior. Both are stronger forms of continuity than simple pointwise continuity, providing guarantees on the function's smoothness and limiting oscillations uniformly over the domain.
Fundamental Differences: Hölder Versus Uniform Continuity
Holder continuity generalizes uniform continuity by allowing a function \( f \) to satisfy the inequality \( |f(x) - f(y)| \leq C|x - y|^\alpha \) for some constant \( C > 0 \) and exponent \( 0 < \alpha \leq 1 \), which quantifies smoothness and local behavior more precisely. Uniform continuity requires the function's oscillation to be controlled uniformly over the domain without involving an exponent, ensuring that for every \( \varepsilon > 0 \), a single \( \delta > 0 \) works for all points to maintain \( |f(x) - f(y)| < \varepsilon \) whenever \( |x - y| < \delta \). Holder continuity is stronger than uniform continuity when \( \alpha = 1 \) corresponds to Lipschitz continuity, and for \( \alpha < 1 \), it captures fractional smoothness that uniform continuity alone cannot describe.
Real-world Examples of Hölder Continuous Functions
Holder continuous functions appear in real-world applications such as modeling turbulent fluid flows, where velocity fields exhibit fractional smoothness characterized by Holder conditions with exponents less than one. Image processing algorithms use Holder continuity to handle textures with varying degrees of roughness, ensuring stable feature detection under noise. In financial mathematics, asset price models incorporate Holder continuous paths to capture irregular market fluctuations more accurately than uniformly continuous models.
Practical Examples of Uniformly Continuous Functions
Uniformly continuous functions maintain a consistent rate of change across their entire domain, ensuring that for every e > 0, there exists a d > 0 independent of the point, which contrasts with Holder continuity where the rate varies with distance raised to a power a (0 < a <= 1). Practical examples of uniformly continuous functions include linear functions like f(x) = 2x, trigonometric functions such as sine and cosine on the real line, and bounded continuous functions on closed intervals like f(x) = x on [0,1]. These examples demonstrate that uniform continuity guarantees control over function oscillation without dependence on localized behavior, making it critical in numerical analysis and approximation theory.
Applications and Significance in Analysis
Holder continuity, characterized by the inequality |f(x)-f(y)| <= C|x-y|^a for 0 < a <= 1, plays a crucial role in partial differential equations and fractal geometry by providing a precise measure of function regularity and smoothness beyond uniform continuity. Uniform continuity ensures that the function's behavior is controlled uniformly over its entire domain, which is fundamental in analysis for extending functions, integration theory, and guaranteeing the convergence of function sequences on compact sets. The stronger constraints of Holder continuity enable finer control in numerical analysis and the study of solution stability, making it indispensable in functional analysis and various applied mathematical models.
Summary: Comparing Hölder and Uniform Continuity
Holder continuity generalizes uniform continuity by introducing an exponent \( \alpha \in (0,1] \) controlling the function's smoothness, allowing for more flexible but less strict constraints. Uniform continuity requires the difference in function values to be bounded by any small \( \epsilon > 0 \) uniformly over the domain, implying Holder continuity with \( \alpha = 1 \). Holder continuity with \( \alpha < 1 \) still guarantees continuity but permits functions with slower rates of change than those uniformly continuous.
Holder continuity Infographic
 libterm.com
libterm.com