Maximizing productivity requires understanding key strategies that align with your personal workflow and goals. Implementing effective time management techniques can significantly enhance your efficiency and reduce stress. Explore the rest of this article to discover practical tips tailored to boost your performance.
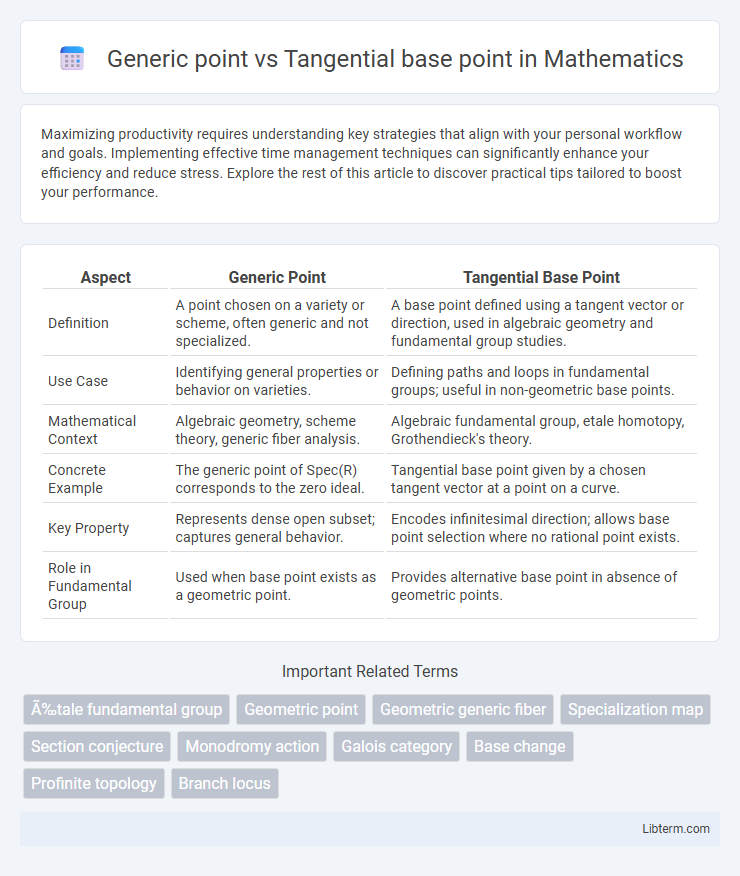
Table of Comparison
| Aspect | Generic Point | Tangential Base Point |
|---|---|---|
| Definition | A point chosen on a variety or scheme, often generic and not specialized. | A base point defined using a tangent vector or direction, used in algebraic geometry and fundamental group studies. |
| Use Case | Identifying general properties or behavior on varieties. | Defining paths and loops in fundamental groups; useful in non-geometric base points. |
| Mathematical Context | Algebraic geometry, scheme theory, generic fiber analysis. | Algebraic fundamental group, etale homotopy, Grothendieck's theory. |
| Concrete Example | The generic point of Spec(R) corresponds to the zero ideal. | Tangential base point given by a chosen tangent vector at a point on a curve. |
| Key Property | Represents dense open subset; captures general behavior. | Encodes infinitesimal direction; allows base point selection where no rational point exists. |
| Role in Fundamental Group | Used when base point exists as a geometric point. | Provides alternative base point in absence of geometric points. |
Introduction to Base Points in Mathematics
Generic points represent the most general elements of a variety, capturing typical properties without specialization, while tangential base points arise in the study of fundamental groups and are associated with tangent directions at singularities or boundary points. Base points serve as fixed reference points in algebraic geometry and topology, facilitating the study of morphisms, fundamental groups, and covering spaces. Understanding the distinction clarifies how geometric and topological structures behave locally versus at more generalized or generic positions.
Understanding the Generic Point
The generic point in algebraic geometry is a fundamental concept representing the "most general" element of a scheme, capturing the generic behavior of the structure without specializing to any closed point. It corresponds to the minimal prime ideal and serves as a universal base point for properties valid on dense open subsets. Understanding the generic point is crucial for studying local-global principles and formulating geometric intuition beyond tangential or specialized base points.
Defining the Tangential Base Point
A tangential base point is a concept in algebraic geometry used to define fiber functors on the etale fundamental group by specifying a tangent direction at a point, rather than the point itself. Unlike a generic point, which corresponds to a dense open subset of a scheme, a tangential base point captures infinitesimal paths approaching a singularity or boundary, enabling the study of local monodromy phenomena. This notion refines classical base points by incorporating differential data, crucial for understanding the fundamental group in the presence of singularities or ramification.
Key Differences Between Generic and Tangential Base Points
Generic base points represent general or "typical" positions within algebraic geometry, often corresponding to dense open subsets, while tangential base points arise from specifying a tangent direction at a given point, capturing infinitesimal data. Key differences include their topological interpretation--generic base points reflect generic position without fixing direction, whereas tangential base points incorporate directional information, enabling finer distinctions in fundamental group computations. The choice between generic and tangential base points significantly impacts the study of etale fundamental groups and monodromy representations by influencing how coverings and paths are analyzed.
Importance of Base Points in Algebraic Geometry
Base points play a crucial role in algebraic geometry by anchoring the study of morphisms and families of algebraic varieties, with generic points representing the most general location in a variety used for defining general properties. Tangential base points offer refined local information by incorporating directions and infinitesimal data, essential for understanding the behavior of varieties near singularities or special loci. The choice between generic and tangential base points impacts the construction of fundamental groups and the analysis of deformation spaces, highlighting their significance in complex geometric and topological investigations.
Applications of Generic Points
Generic points serve as fundamental tools in algebraic geometry for studying the properties of algebraic varieties by representing the most general element in a variety's underlying topological space. In contrast, tangential base points are used in the theory of fundamental groups and covering spaces to analyze paths and loops at infinitesimally small neighborhoods, often in arithmetic geometry contexts. Applications of generic points include simplifying the examination of function fields, facilitating the proof of key theorems on irreducibility, and enabling the extension of geometric properties across dense subsets of algebraic varieties.
Use Cases for Tangential Base Points
Tangential base points are essential in algebraic geometry and number theory for defining fundamental groups and motivic Galois groups when standard geometric points are unavailable or insufficient. Use cases include studying the etale fundamental group of schemes over fields with incomplete or complicated point sets, such as in the theory of motives or the Grothendieck-Teichmuller group. Tangential base points facilitate consistent path and monodromy definitions in these contexts, enabling advanced computations and comparisons between different fiber functors.
Base Points in Fundamental Group Theory
In fundamental group theory, a generic base point is typically any chosen point on a topological space from which loops are based and homotopy classes are considered, while a tangential base point arises from algebraic geometry and incorporates infinitesimal data near a point to define paths in more refined contexts. Tangential base points enable the study of fundamental groups in situations where a conventional point may not be accessible, such as in schemes or algebraic varieties over fields without rational points. The distinction impacts the construction of fundamental groups by allowing tangential base points to encode additional geometric information essential for understanding monodromy and coverings in arithmetic geometry.
Advantages and Limitations of Each Approach
Generic points offer a flexible framework for studying algebraic varieties by representing typical behavior through points defined over algebraically closed fields, enabling broad applicability in geometric contexts. Tangential base points provide a refined tool in fundamental group analysis by incorporating tangent vector data, allowing for enhanced control over path lifting and monodromy computations in etale fundamental groups. The generic point approach may lack precision in capturing local geometric nuances, while tangential base points can be more complex to construct and require additional structure, limiting their direct use in certain global geometric problems.
Summary: Choosing the Right Base Point
Selecting the appropriate base point between generic and tangential types hinges on the algebraic geometry context and specific problem requirements. Generic base points are broadly applicable and often used in moduli problems due to their general position and simplicity, while tangential base points provide finer control in deformation theory and local monodromy analyses by capturing tangent direction data. The choice directly impacts computational tractability and the granularity of geometric or topological invariants obtained.
Generic point Infographic
 libterm.com
libterm.com