Symmetry groups describe the set of all transformations that preserve the structure of a geometric object, playing a crucial role in mathematics and physics. Understanding these groups helps you analyze patterns, solve equations, and explore spatial relationships. Dive into the rest of the article to discover how symmetry groups influence various scientific fields.
Table of Comparison
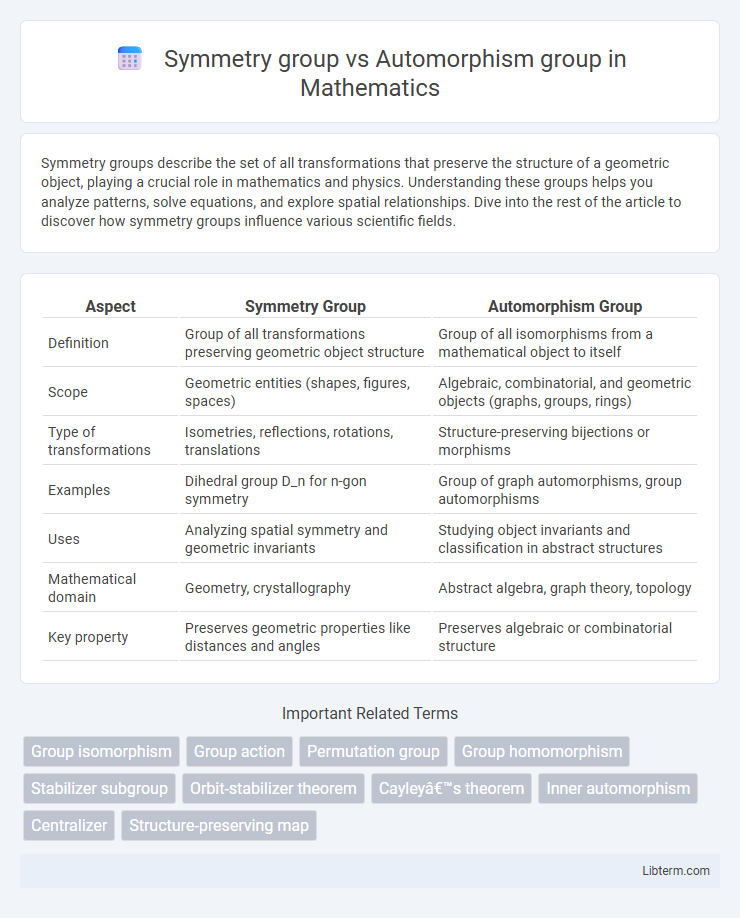
| Aspect | Symmetry Group | Automorphism Group |
|---|---|---|
| Definition | Group of all transformations preserving geometric object structure | Group of all isomorphisms from a mathematical object to itself |
| Scope | Geometric entities (shapes, figures, spaces) | Algebraic, combinatorial, and geometric objects (graphs, groups, rings) |
| Type of transformations | Isometries, reflections, rotations, translations | Structure-preserving bijections or morphisms |
| Examples | Dihedral group D_n for n-gon symmetry | Group of graph automorphisms, group automorphisms |
| Uses | Analyzing spatial symmetry and geometric invariants | Studying object invariants and classification in abstract structures |
| Mathematical domain | Geometry, crystallography | Abstract algebra, graph theory, topology |
| Key property | Preserves geometric properties like distances and angles | Preserves algebraic or combinatorial structure |
Introduction to Symmetry Groups and Automorphism Groups
Symmetry groups consist of all transformations preserving the structure of a geometric object, encoding its inherent symmetries through operations like rotations and reflections. Automorphism groups generalize this concept by encompassing all isomorphisms from a mathematical structure onto itself, preserving algebraic or combinatorial properties. Understanding the distinction highlights how symmetry groups focus on geometric invariances while automorphism groups capture structural self-equivalences across diverse mathematical contexts.
Defining Symmetry Groups: Key Concepts
Symmetry groups consist of all the transformations, such as rotations and reflections, that preserve the structure of a geometric object or mathematical system. The automorphism group generalizes this concept to abstract algebraic structures, capturing all isomorphisms from the structure to itself that maintain its core operations and relations. Defining symmetry groups involves identifying invariances under group actions, while automorphism groups emphasize structural self-equivalences in algebraic settings.
Understanding Automorphism Groups
Automorphism groups capture the symmetries of mathematical structures by describing all isomorphisms from the structure to itself, preserving its defining properties. Unlike symmetry groups that often represent geometric or physical symmetries, automorphism groups generalize these concepts to algebraic objects such as graphs, groups, or fields. Understanding automorphism groups involves analyzing how internal structure transformations maintain invariants, crucial for classification problems and in fields like group theory, topology, and algebraic geometry.
Mathematical Foundations: Group Theory Essentials
Symmetry groups consist of transformations preserving an object's structure, forming a group under composition that captures geometric invariances. Automorphism groups generalize this concept by including all isomorphisms from a mathematical structure to itself, reflecting symmetries in algebraic and combinatorial contexts. Both groups embody fundamental principles in group theory, emphasizing closure, inverses, and identity to model intrinsic symmetry properties across diverse mathematical systems.
Distinguishing Features: Symmetry vs Automorphism
Symmetry groups consist of transformations that preserve geometric objects' shape and structure, such as rotations and reflections, maintaining spatial properties. Automorphism groups, however, encompass all isomorphisms from a mathematical structure onto itself, preserving algebraic or relational properties beyond mere geometric configurations. This fundamental distinction highlights symmetry groups as subsets of automorphism groups focused on spatial symmetry, while automorphism groups apply to a broader range of abstract structures like graphs, groups, and fields.
Examples of Symmetry Groups in Geometry
Symmetry groups in geometry describe sets of isometries preserving a figure, such as the dihedral group \(D_n\), representing symmetries of a regular n-gon, combining rotations and reflections. Automorphism groups extend this concept to abstract mathematical structures, like graphs or algebraic objects, where automorphisms are isomorphisms from a structure to itself preserving its defining relations. For example, the automorphism group of a cube includes all rotational symmetries, coinciding with the group \(S_4\) acting on its four space diagonals, reflecting its geometric and combinatorial symmetries.
Automorphism Groups in Algebraic Structures
Automorphism groups in algebraic structures consist of all isomorphisms from the structure onto itself, preserving operations and relations, which makes them fundamental in studying the internal symmetries of algebraic objects like groups, rings, and fields. These groups reveal invariant properties and structure-preserving transformations that help classify and understand the algebraic object's behavior under symmetry operations. Unlike symmetry groups that often describe geometric symmetries, automorphism groups are abstract algebraic frameworks capturing symmetries at the level of algebraic structure.
Applications of Symmetry and Automorphism Groups
Symmetry groups classify geometric transformations preserving object structure, playing a crucial role in crystallography, molecular chemistry, and physics for analyzing spatial symmetries and predicting physical properties. Automorphism groups describe structure-preserving mappings within abstract algebraic or combinatorial objects, essential in graph theory, coding theory, and network analysis to detect symmetry and optimize configuration. Both groups fundamentally enable simplification and classification in diverse mathematical models and practical applications such as robotics, cryptography, and pattern recognition.
Symmetry and Automorphism in Real-World Contexts
Symmetry groups describe transformations preserving the structure of geometric objects, playing a crucial role in crystallography, physics, and molecular biology by modeling spatial symmetries. Automorphism groups extend this concept to abstract algebraic structures, preserving operations and relations within graphs, networks, and algebraic systems, which informs fields like network theory and coding. Understanding both groups enhances the analysis of real-world patterns, system invariances, and structural integrity across science and engineering.
Summary: Key Differences and Similarities
The symmetry group of a mathematical object consists of all transformations preserving its structural properties, typically focusing on geometric or spatial symmetries. The automorphism group generalizes this concept by including all isomorphisms from the object to itself that preserve its entire algebraic structure, such as group operations or graph connections. Both groups capture the idea of structure-preserving transformations, but the automorphism group applies to a broader range of objects beyond geometric figures, encompassing algebraic, combinatorial, and topological structures.
Symmetry group Infographic
 libterm.com
libterm.com