Absolute homology is a fundamental concept in algebraic topology that studies the structure of topological spaces by associating algebraic objects, such as groups, to them. It provides a way to classify and measure holes or voids within a space through cycles and boundaries. Explore the rest of this article to understand how absolute homology reveals deep insights into the shape and connectivity of your topological spaces.
Table of Comparison
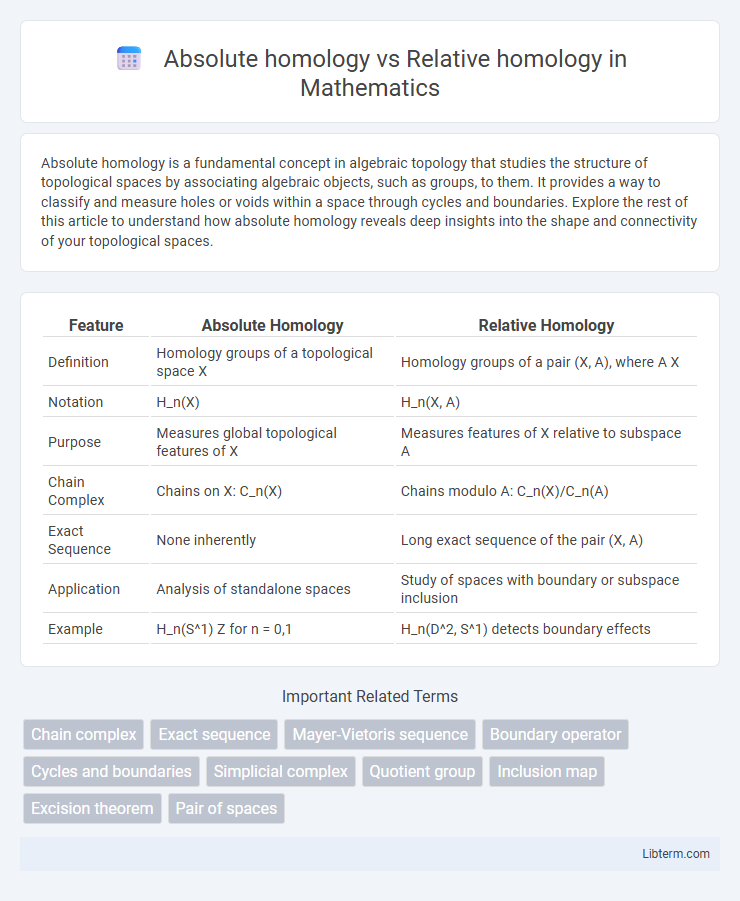
| Feature | Absolute Homology | Relative Homology |
|---|---|---|
| Definition | Homology groups of a topological space X | Homology groups of a pair (X, A), where A X |
| Notation | H_n(X) | H_n(X, A) |
| Purpose | Measures global topological features of X | Measures features of X relative to subspace A |
| Chain Complex | Chains on X: C_n(X) | Chains modulo A: C_n(X)/C_n(A) |
| Exact Sequence | None inherently | Long exact sequence of the pair (X, A) |
| Application | Analysis of standalone spaces | Study of spaces with boundary or subspace inclusion |
| Example | H_n(S^1) Z for n = 0,1 | H_n(D^2, S^1) detects boundary effects |
Introduction to Homology in Topology
Absolute homology studies topological spaces by analyzing their homology groups, which classify holes of various dimensions within a single space. Relative homology, on the other hand, examines pairs of spaces \((X, A)\), focusing on how the inclusion of a subspace \(A\) affects the homological features of \(X\). Both concepts provide algebraic tools to capture the structure of spaces, with relative homology offering finer insight by measuring the differences between a space and its subspace.
Defining Absolute Homology
Absolute homology measures the algebraic structure of a topological space by analyzing chains, cycles, and boundaries within the entire space, providing information about holes of different dimensions. It is defined as the quotient of the cycle group by the boundary group, capturing topological features invariant under continuous deformations. Relative homology, in contrast, studies pairs of spaces, focusing on the homological properties of a space relative to a subspace, thus refining the understanding of local topological differences.
Understanding Relative Homology
Relative homology measures the homology groups of a pair of topological spaces (X, A) where A is a subspace of X, capturing how cycles in X that lie outside A behave relative to A. This concept extends absolute homology by focusing on the quotient of chain complexes, allowing for analysis of features that may become trivial when restricted to A, thus providing insight into the structure of spaces with boundary or inclusions. Understanding relative homology is crucial for applications in algebraic topology, such as excision, Mayer-Vietoris sequences, and the study of manifolds with boundary.
Key Differences Between Absolute and Relative Homology
Absolute homology measures the intrinsic topological features of a single space by analyzing its cycles and boundaries across dimensions, while relative homology evaluates these features in relation to a subspace, capturing how the larger space's topology changes when the subspace is considered. The key difference lies in absolute homology focusing on the entire space's homological groups H_n(X), whereas relative homology concerns the quotient groups H_n(X, A) that measure the homology classes of X modulo those of the subspace A. Relative homology enables the study of topological features that vanish or appear when a subspace is included, making it essential for understanding inclusion maps and boundary behavior in algebraic topology.
Mathematical Formulation of Absolute Homology
Absolute homology is formulated by constructing a chain complex \( C_n(X) \) from singular \( n \)-simplices in a topological space \( X \), and then computing homology groups \( H_n(X) = \ker \partial_n / \operatorname{im} \partial_{n+1} \), where \( \partial_n \) are boundary operators. These homology groups capture topological invariants such as holes and connected components intrinsic to the space \( X \) itself. Relative homology \( H_n(X, A) \) generalizes this by analyzing the pair \( (X, A) \) with \( A \subseteq X \), focusing on features of \( X \) modulo the subspace \( A \).
Mathematical Formulation of Relative Homology
Relative homology is defined using the homology groups of a pair of topological spaces (X, A), where A is a subspace of X, and is computed as the homology of the quotient complex C_*(X)/C_*(A). The mathematical formulation involves the long exact sequence of homology groups derived from the short exact sequence of chain complexes 0 - C_*(A) - C_*(X) - C_*(X, A) - 0, which relates absolute homology groups H_n(A) and H_n(X) to the relative homology groups H_n(X, A). Relative homology captures the features of space X that are not present in subspace A, making it instrumental in algebraic topology for studying space pairs.
Applications of Absolute Homology
Absolute homology plays a crucial role in algebraic topology by providing a way to classify and analyze the intrinsic shapes and structures of topological spaces without reference to a subspace. Applications include identifying holes, voids, and connected components in data analysis, studying the fundamental group, and aiding in mesh generation in computer graphics. Its utility extends to sensor networks, robotics, and image processing where understanding the global topological features is essential.
Applications of Relative Homology
Relative homology plays a crucial role in algebraic topology by allowing the study of topological spaces with subspaces, which is essential for understanding complex shapes and their features. It finds applications in areas such as persistent homology in data analysis, where it helps identify and classify features that persist across multiple scales. Furthermore, relative homology is instrumental in manifold theory and boundary value problems, enabling the examination of properties of spaces relative to their boundaries.
The Role of Exact Sequences in Homology
Exact sequences play a crucial role in comparing absolute and relative homology by providing algebraic tools to analyze the change in homology groups when passing from a space to a subspace. The long exact sequence of a pair (X, A) links the absolute homology groups of X and A with the relative homology groups H_n(X, A), enabling computation of relative homology from known absolute homology data. This framework reveals the algebraic structure governing inclusion maps and boundary operators, offering key insights into topological invariants and their interrelations.
Comparative Analysis: Choosing Between Absolute and Relative Homology
Absolute homology measures the exact degree of similarity between sequences by calculating shared ancestry, making it ideal for studies requiring precise evolutionary relationships. Relative homology compares homology levels relative to other sequences, which is effective for identifying functional similarities among gene families without strict evolutionary constraints. Choosing between absolute and relative homology depends on whether the goal is to establish precise phylogenetic connections or to infer functional relationships in diverse biological contexts.
Absolute homology Infographic
 libterm.com
libterm.com