Eilenberg-MacLane spectra are fundamental objects in stable homotopy theory, representing ordinary cohomology theories associated with abelian groups. They provide a bridge between algebraic structures and topological spaces, allowing computations of homotopy groups via homology and cohomology. Explore the article to deepen your understanding of how Eilenberg-MacLane spectra shape modern algebraic topology.
Table of Comparison
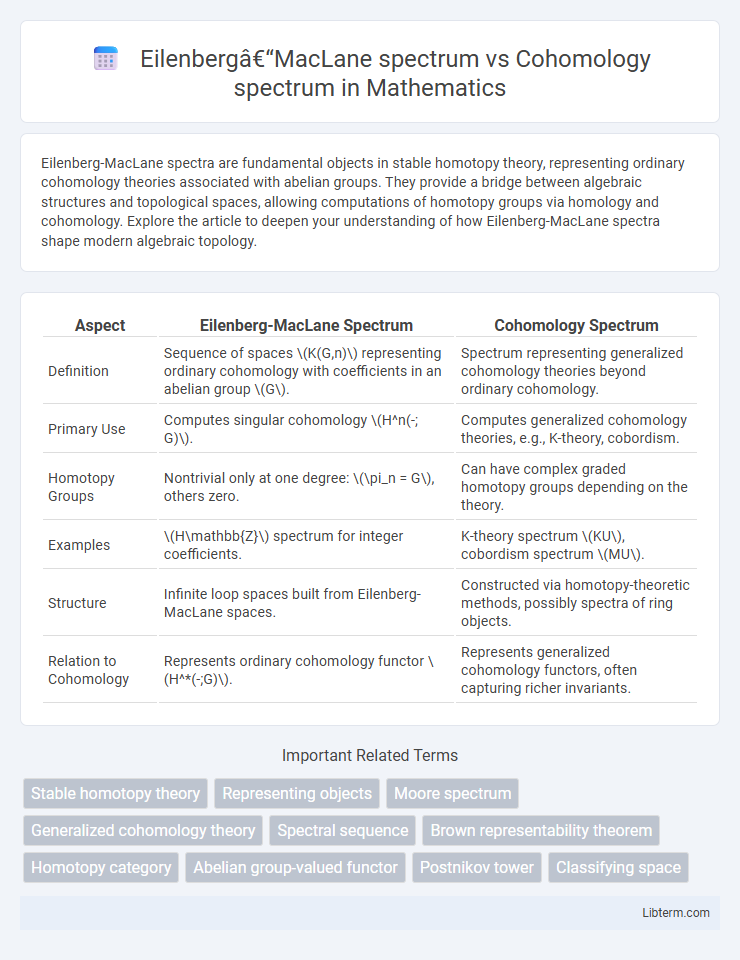
| Aspect | Eilenberg-MacLane Spectrum | Cohomology Spectrum |
|---|---|---|
| Definition | Sequence of spaces \(K(G,n)\) representing ordinary cohomology with coefficients in an abelian group \(G\). | Spectrum representing generalized cohomology theories beyond ordinary cohomology. |
| Primary Use | Computes singular cohomology \(H^n(-; G)\). | Computes generalized cohomology theories, e.g., K-theory, cobordism. |
| Homotopy Groups | Nontrivial only at one degree: \(\pi_n = G\), others zero. | Can have complex graded homotopy groups depending on the theory. |
| Examples | \(H\mathbb{Z}\) spectrum for integer coefficients. | K-theory spectrum \(KU\), cobordism spectrum \(MU\). |
| Structure | Infinite loop spaces built from Eilenberg-MacLane spaces. | Constructed via homotopy-theoretic methods, possibly spectra of ring objects. |
| Relation to Cohomology | Represents ordinary cohomology functor \(H^*(-;G)\). | Represents generalized cohomology functors, often capturing richer invariants. |
Introduction to Eilenberg–MacLane and Cohomology Spectra
Eilenberg-MacLane spectra represent fundamental objects in stable homotopy theory characterized by having a single nontrivial homotopy group, typically denoted as \( K(G, n) \) for an abelian group \( G \) and integer \( n \). Cohomology spectra extend this concept by encoding generalized cohomology theories associated with specific spectra, allowing computation of cohomology groups via homotopy classes of maps into these spectra. Understanding Eilenberg-MacLane spectra provides a foundational framework for defining and analyzing cohomology spectra, connecting algebraic invariants to topological spaces through stable homotopy categories.
Historical Background and Motivation
The Eilenberg-MacLane spectrum, introduced in the 1950s, emerged from efforts to represent singular cohomology theories as generalized cohomology theories in stable homotopy theory. Its construction enabled algebraic topologists to translate cohomological problems into stable homotopy-theoretic contexts, providing a foundational tool for spectral sequence calculations. The cohomology spectrum generalizes this concept by representing various cohomology theories, motivated by the need to systematically study cohomological operations and generalized (extraordinary) cohomology theories beyond singular cohomology, facilitating deeper connections between homotopy theory and algebraic invariants.
Defining Eilenberg–MacLane Spectra
Eilenberg-MacLane spectra serve as foundational objects in stable homotopy theory, characterized by their unique property of having a single nontrivial homotopy group concentrated in one degree. They are constructed to represent ordinary cohomology theories with coefficients in an abelian group, providing a bridge between algebraic topology and homological algebra. These spectra are defined by assigning spaces K(G, n), called Eilenberg-MacLane spaces, whose homotopy groups satisfy p_n(K(G, n)) = G and p_k(K(G, n)) = 0 for k n, enabling the realization of cohomology spectra as generalized cohomology theories represented by these spectra.
Understanding Cohomology Spectra
Cohomology spectra generalize classical cohomology theories by representing cohomology groups as homotopy classes of maps into carefully structured spectra, providing a unifying framework for various cohomological invariants. The Eilenberg-MacLane spectrum serves as a fundamental example, representing ordinary cohomology theories with coefficients in abelian groups via spaces \( K(G,n) \), which encapsulate the nth cohomology group \( H^n(X; G) \) in the stable homotopy category. Understanding cohomology spectra involves analyzing how these spectra encode cohomological information through stable homotopy types, enabling extensions to generalized cohomology theories beyond classical Eilenberg-MacLane constructions.
Key Differences Between Eilenberg–MacLane and Cohomology Spectra
The Eilenberg-MacLane spectrum is primarily constructed to represent singular cohomology with a fixed coefficient group, making it a fundamental object in stable homotopy theory. In contrast, cohomology spectra generalize this concept by encoding various generalized cohomology theories beyond ordinary cohomology, often involving more complex or structured ring spectra. Key differences include the Eilenberg-MacLane spectrum's role as a universal coefficient object for discrete abelian groups, whereas cohomology spectra encompass broader algebraic and topological invariants applicable to diverse cohomology frameworks.
Algebraic Topology Applications
Eilenberg-MacLane spectra represent ordinary cohomology theories associated with an abelian group, serving as fundamental building blocks in stable homotopy theory and algebraic topology applications. Cohomology spectra generalize these ideas, enabling the study of generalized cohomology theories such as K-theory and complex cobordism, which capture richer algebraic structures and invariants of topological spaces. Their interplay facilitates the computation of homotopy groups, classification of fiber bundles, and understanding of spectral sequences and characteristic classes in algebraic topology.
Examples and Constructions in Stable Homotopy Theory
The Eilenberg-MacLane spectrum \( H\mathbb{Z} \) serves as a fundamental example in stable homotopy theory, representing ordinary cohomology with integer coefficients and constructed via a sequence of Eilenberg-MacLane spaces \( K(\mathbb{Z}, n) \) with structure maps inducing suspension isomorphisms. Cohomology spectra generalize this concept by representing various generalized cohomology theories, such as complex K-theory through the spectrum \( KU \) or cobordism theories with the \( MU \) spectrum, each constructed using sophisticated tools like Thom spaces or loop space machines. These constructions connect algebraic invariants to stable homotopy types, allowing explicit calculations of homotopy groups and facilitating computations in the Adams spectral sequence or other spectral methods.
Functorial Properties and Universality
Eilenberg-MacLane spectra exhibit strong functorial properties as they represent ordinary cohomology theories and serve as universal targets in homotopy categories, enabling natural transformations corresponding to cohomology operations. Cohomology spectra generalize these constructs by encoding generalized cohomology theories functorially, capturing richer algebraic invariants with universal mapping properties reflecting higher homotopical structures. The universality of Eilenberg-MacLane spectra underpins their role as initial objects among spectra representing ordinary cohomology, while cohomology spectra realize broader universality in representing diverse cohomological functors through structured ring spectra.
Implications in Modern Mathematical Research
Eilenberg-MacLane spectra represent ordinary cohomology theories and serve as foundational building blocks in stable homotopy theory, enabling explicit calculations of homotopy groups and facilitating the classification of cohomology operations. Cohomology spectra, extending beyond Eilenberg-MacLane constructions, encode generalized cohomology theories that capture deeper geometric and topological invariants, influencing areas such as chromatic homotopy theory and motivic homotopy theory. The interplay between these spectra advances research in algebraic topology by providing tools to systematically analyze structured ring spectra, spectral sequences, and higher category theory frameworks.
Conclusion: Comparative Insights and Future Directions
Eilenberg-MacLane spectra serve as fundamental building blocks in stable homotopy theory, representing ordinary cohomology theories with abelian group coefficients and enabling explicit calculations. In contrast, cohomology spectra generalize this concept, encompassing a broader class of generalized cohomology theories that capture richer topological information beyond classical invariants. Future research aims to deepen the understanding of interactions between these spectra, explore computational frameworks for complex cohomology theories, and develop new categorical structures linking them to modern homotopical and algebraic contexts.
Eilenberg–MacLane spectrum Infographic
 libterm.com
libterm.com