A vector bundle is a topological construction that assigns a vector space to each point of a base space, allowing for the systematic study of linear algebra in varying contexts. It plays a crucial role in differential geometry and topology, enabling the examination of fields like tangent bundles and fiber bundles. Explore the rest of this article to deepen your understanding of how vector bundles function and their applications in mathematics.
Table of Comparison
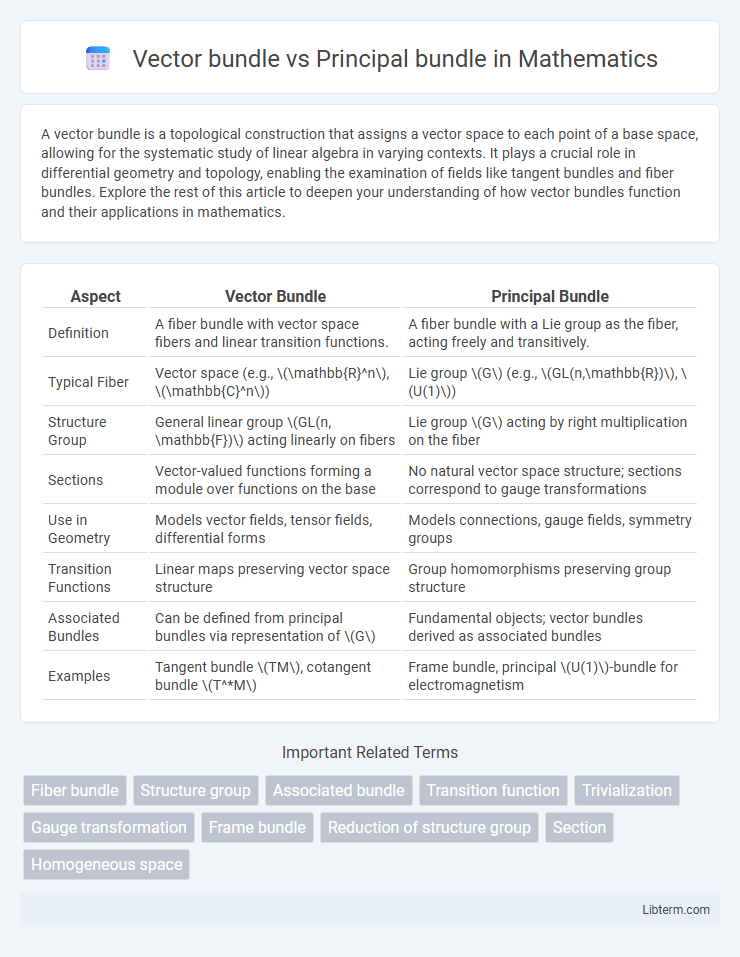
| Aspect | Vector Bundle | Principal Bundle |
|---|---|---|
| Definition | A fiber bundle with vector space fibers and linear transition functions. | A fiber bundle with a Lie group as the fiber, acting freely and transitively. |
| Typical Fiber | Vector space (e.g., \(\mathbb{R}^n\), \(\mathbb{C}^n\)) | Lie group \(G\) (e.g., \(GL(n,\mathbb{R})\), \(U(1)\)) |
| Structure Group | General linear group \(GL(n, \mathbb{F})\) acting linearly on fibers | Lie group \(G\) acting by right multiplication on the fiber |
| Sections | Vector-valued functions forming a module over functions on the base | No natural vector space structure; sections correspond to gauge transformations |
| Use in Geometry | Models vector fields, tensor fields, differential forms | Models connections, gauge fields, symmetry groups |
| Transition Functions | Linear maps preserving vector space structure | Group homomorphisms preserving group structure |
| Associated Bundles | Can be defined from principal bundles via representation of \(G\) | Fundamental objects; vector bundles derived as associated bundles |
| Examples | Tangent bundle \(TM\), cotangent bundle \(T^*M\) | Frame bundle, principal \(U(1)\)-bundle for electromagnetism |
Introduction to Vector Bundles and Principal Bundles
Vector bundles are topological constructions where a vector space is attached smoothly to each point of a base space, allowing linear algebraic operations within fibers that vary continuously. Principal bundles consist of a base space paired with a fiber that is a Lie group, encoding symmetries and enabling the definition of connections used in gauge theories. Both bundles serve as fundamental tools in differential geometry, with vector bundles facilitating the study of sections and linear structures, while principal bundles focus on group actions and the geometric framework of gauge fields.
Foundational Definitions and Key Concepts
Vector bundles are fiber bundles where each fiber is a vector space, equipped with linear transition functions preserving the vector space structure. Principal bundles consist of fibers modeled on a Lie group, with group actions defining the bundle's structural symmetry and compatibility conditions. Both structures form essential frameworks in differential geometry, with vector bundles facilitating linear algebraic operations on manifolds while principal bundles encode gauge symmetries and connections.
Structure Groups: Comparison and Roles
Vector bundles have structure groups typically given by the general linear group GL(n, R) or GL(n, C), which act linearly on vector spaces, defining the fiber's linear structure. Principal bundles feature more general structure groups G, often Lie groups, that act freely and transitively on the fibers, serving as the framework for associated bundles and gauge fields. The structure group in vector bundles dictates linear transformations preserving vector space structures, whereas in principal bundles, it encodes symmetries and forms the basis for connections and curvature in differential geometry.
Local Trivializations in Vector vs. Principal Bundles
Local trivializations in vector bundles consist of homeomorphisms mapping the bundle locally to a product of an open subset of the base space and a vector space, preserving the linear structure on fibers. In principal bundles, local trivializations correspond to homeomorphisms to a product of an open subset and the structure group, respecting the group action on the fibers. The key distinction lies in the vector bundle's linear fiber structure versus the principal bundle's group action, influencing the choice of transition functions as linear isomorphisms for vector bundles and group elements for principal bundles.
Morphisms and Bundle Maps: Similarities and Differences
Morphisms of vector bundles are bundle maps that preserve the linear structure on each fiber, intertwining linear transformations with base space maps, whereas principal bundle morphisms respect the group action, ensuring equivariance with respect to the structure group. Both vector and principal bundle morphisms induce smooth maps between total spaces covering continuous maps between base manifolds, but vector bundle morphisms act linearly on fibers, while principal bundle morphisms correspond to group-equivariant diffeomorphisms. This difference fundamentally reflects the algebraic structure of fibers: vector spaces for vector bundles versus principal homogeneous spaces for principal bundles.
Associated Bundles and Their Construction
Vector bundles and principal bundles differ fundamentally in structure, with principal bundles having a Lie group as the fiber and vector bundles modeled on vector spaces. Associated bundles arise by taking a principal G-bundle and a representation of G on a vector space V, then constructing the vector bundle as the quotient of the product of the principal bundle and V by the diagonal action of G. This construction allows the translation of information and geometric structures from the principal bundle to the vector bundle, making associated bundles crucial for differential geometry and gauge theory.
Transition Functions and Their Properties
Transition functions of vector bundles map overlaps of local trivializations to GL(n, R) or GL(n, C), ensuring linearity and compatibility with vector space structures. Principal bundles have transition functions valued in a Lie group G, encoding the fiber's symmetry and satisfying the cocycle condition for consistent patching. These transition functions characterize the bundle's topology and induce associated bundles through group representations.
Applications in Geometry and Physics
Vector bundles provide a framework for modeling fields and sections in differential geometry, facilitating the study of tangent spaces, tensor fields, and spinor fields essential in general relativity and gauge theories. Principal bundles underpin gauge theories by encoding symmetry groups and connections, crucial for describing fiber bundles with group actions in quantum field theory and particle physics. Both structures enable rigorous formulations of curvature, holonomy, and gauge transformations, bridging geometric intuition with physical phenomena like electromagnetism and Yang-Mills theory.
Characteristic Classes and Bundle Invariants
Characteristic classes in vector bundles, such as Chern, Stiefel-Whitney, and Pontryagin classes, provide topological invariants describing the twisting and geometry of the bundle's fibers. Principal bundles generalize this concept by associating characteristic classes through the curvature of connections, often via the Chern-Weil homomorphism, linking the bundle's structure group to cohomology classes. Bundle invariants derived from these characteristic classes serve to classify vector bundles up to isomorphism and principal bundles up to gauge equivalence, playing a crucial role in differential topology and gauge theory.
Summary: Choosing Between Vector and Principal Bundles
Vector bundles associate vector spaces fiberwise to a base manifold, ideal for analyzing linear structures and sections such as fields in differential geometry. Principal bundles link fibers with a Lie group acting freely and transitively, serving as the foundation for gauge theories and connections in fiber bundle theory. Selecting between vector and principal bundles depends on whether the focus is on linear representations (vector bundles) or symmetry group actions and structural group properties (principal bundles).
Vector bundle Infographic
 libterm.com
libterm.com