Derived functors play a crucial role in homological algebra by extending the concept of functors to capture hidden algebraic structures and relationships beyond the original functor's scope. They allow you to systematically compute and analyze higher-dimensional invariants such as Ext and Tor groups, which reveal deeper properties of modules and chain complexes. Explore the rest of the article to understand how derived functors work and their applications in advanced mathematics.
Table of Comparison
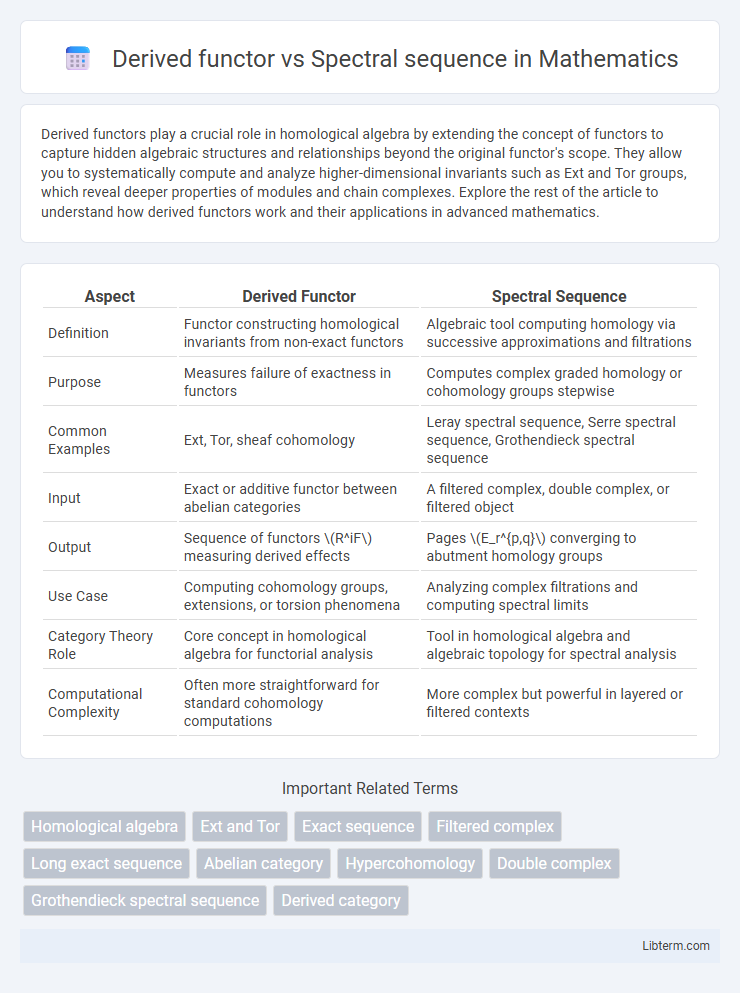
| Aspect | Derived Functor | Spectral Sequence |
|---|---|---|
| Definition | Functor constructing homological invariants from non-exact functors | Algebraic tool computing homology via successive approximations and filtrations |
| Purpose | Measures failure of exactness in functors | Computes complex graded homology or cohomology groups stepwise |
| Common Examples | Ext, Tor, sheaf cohomology | Leray spectral sequence, Serre spectral sequence, Grothendieck spectral sequence |
| Input | Exact or additive functor between abelian categories | A filtered complex, double complex, or filtered object |
| Output | Sequence of functors \(R^iF\) measuring derived effects | Pages \(E_r^{p,q}\) converging to abutment homology groups |
| Use Case | Computing cohomology groups, extensions, or torsion phenomena | Analyzing complex filtrations and computing spectral limits |
| Category Theory Role | Core concept in homological algebra for functorial analysis | Tool in homological algebra and algebraic topology for spectral analysis |
| Computational Complexity | Often more straightforward for standard cohomology computations | More complex but powerful in layered or filtered contexts |
Introduction to Derived Functors
Derived functors extend classical functorial constructions by measuring the failure of exactness, providing deeper insights into homological algebra and cohomology theories. They arise naturally from resolving objects using projective or injective resolutions, enabling the computation of higher cohomology groups. Understanding derived functors lays the groundwork for spectral sequences, which organize complex homological data across multiple filtration levels.
Overview of Spectral Sequences
Spectral sequences provide a powerful computational tool in homological algebra, allowing the step-by-step approximation of complex algebraic invariants such as homology or cohomology groups. They arise from filtered complexes and consist of a sequence of pages, each equipped with differentials that converge to the desired algebraic structure after successive iterations. Unlike derived functors, which directly measure the failure of exactness, spectral sequences decompose complex derived functor calculations into manageable stages, facilitating deep insights into extensions and interactions within algebraic topology and algebraic geometry.
Fundamental Differences Between Derived Functors and Spectral Sequences
Derived functors systematically extend homological algebra to capture higher-dimensional cohomology from exact functor applications, focusing on functorial constructions like Ext and Tor groups. Spectral sequences provide a computational tool to approximate complex homology or cohomology groups through successive approximations, often arising from filtered complexes or double complexes. The fundamental difference lies in derived functors being intrinsic objects capturing homological behavior of functors, while spectral sequences serve as computational frameworks facilitating stepwise analysis of these or other homological invariants.
Motivations for Using Derived Functors
Derived functors provide a systematic approach to extending classical functors to homological contexts by capturing higher-dimensional algebraic information such as Ext and Tor groups. They emerge from the need to analyze exactness properties and compute cohomology in categories lacking sufficient projectiveness or injectiveness. This methodology allows algebraists and topologists to efficiently resolve objects and interpret complex structures that spectral sequences may approximate only incrementally.
Motivations for Employing Spectral Sequences
Spectral sequences are employed to compute complex derived functors when direct calculation is infeasible due to intricate filtration or grading structures. They provide successive approximations that converge to the desired algebraic invariants, enabling stepwise analysis of homological or cohomological data. This approach is particularly motivating in contexts like filtered complexes, where derived functors alone do not easily capture layered structural information.
Technical Definitions and Key Properties
Derived functors extend classical functors to homological algebra contexts by computing right or left derived functors that measure the failure of exactness, typically constructed via injective or projective resolutions. Spectral sequences provide a computational tool to approximate complex homology groups through successive pages (E_r), with differentials d_r and filtrations that converge to the desired graded object or cohomology. Key properties of derived functors include universality and exactness preservation along exact sequences, while spectral sequences are characterized by their filtration convergence, edge morphisms, and exact couples that govern their iterative structure.
Examples Illustrating Derived Functors
Derived functors arise naturally in homological algebra to systematically extend functors, with Ext and Tor serving as classical examples that measure extensions and tensor product torsion between modules. Spectral sequences, often constructed from filtered chain complexes, provide computational tools that approximate these derived functors step-by-step, as seen in the Grothendieck spectral sequence relating compositions of derived functors. For instance, Ext groups can be computed using a spectral sequence derived from a double complex, simplifying complex homological algebra calculations through successive approximations.
Applications of Spectral Sequences in Mathematics
Spectral sequences provide powerful computational tools in algebraic topology, homological algebra, and algebraic geometry by systematically approximating complex homology or cohomology groups through successive pages or differentials. They enable the computation of derived functors such as Ext and Tor groups when direct calculation is challenging, bridging gaps in exact sequences and filtrations. Applications include analyzing sheaf cohomology, stable homotopy groups, and the study of fibrations, thus extending the reach of derived functor techniques in intricate contexts.
Interactions Between Derived Functors and Spectral Sequences
Derived functors systematically measure the failure of exactness in homological algebra, while spectral sequences provide computational tools to approximate complex homological invariants through filtered complexes. The interaction between derived functors and spectral sequences is crucial in resolving intricate Ext and Tor groups by iteratively refining approximations via convergence properties. Notably, spectral sequences often arise from the composition of derived functors, enabling stepwise calculations in layered homological contexts like filtered chain complexes or double complexes.
Summary and Further Reading
Derived functors generalize homological constructions by extending functors between abelian categories to their derived categories, enabling systematic computation of right or left derived functors such as Ext and Tor. Spectral sequences provide a powerful computational tool to resolve complex filtrations and successive approximations in homological algebra, often converging to the desired (co)homology groups related to derived functors. For further reading, consult Weibel's "An Introduction to Homological Algebra" and McCleary's "A User's Guide to Spectral Sequences" for detailed explanations and illustrative examples.
Derived functor Infographic
 libterm.com
libterm.com