Cohomology provides a powerful algebraic framework for analyzing the properties of topological spaces by associating algebraic invariants to them. It reveals deep relationships between geometry and algebra, enabling you to classify and understand complex structures through tools like cochain complexes and cup products. Explore the rest of the article to discover how cohomology can unlock new insights into mathematical and physical theories.
Table of Comparison
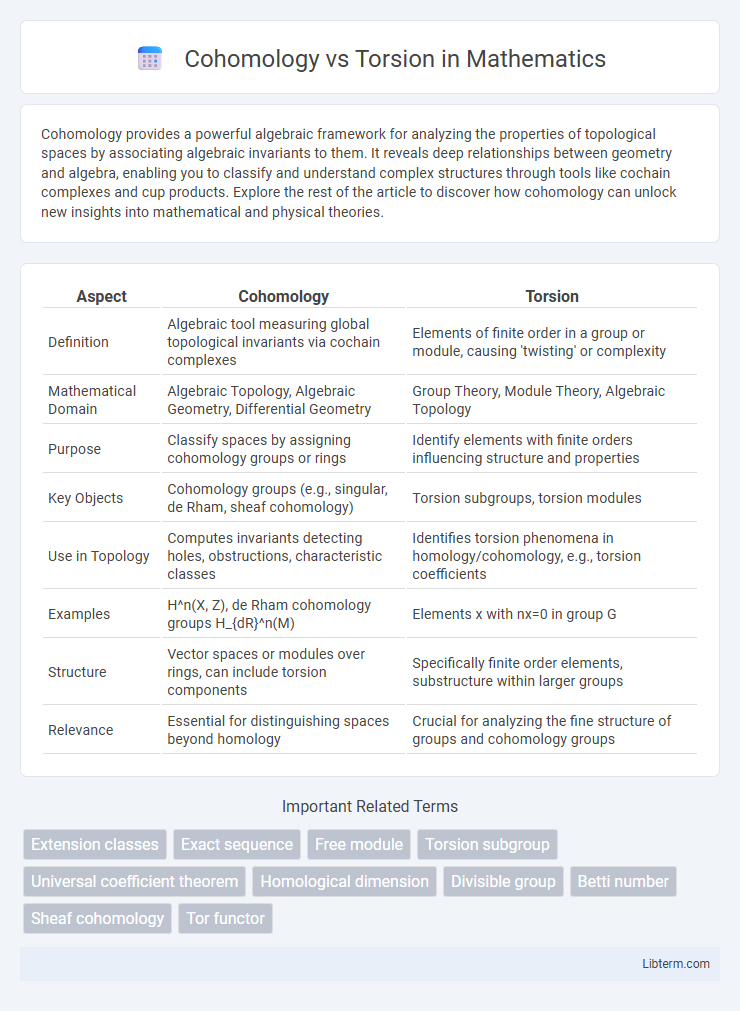
| Aspect | Cohomology | Torsion |
|---|---|---|
| Definition | Algebraic tool measuring global topological invariants via cochain complexes | Elements of finite order in a group or module, causing 'twisting' or complexity |
| Mathematical Domain | Algebraic Topology, Algebraic Geometry, Differential Geometry | Group Theory, Module Theory, Algebraic Topology |
| Purpose | Classify spaces by assigning cohomology groups or rings | Identify elements with finite orders influencing structure and properties |
| Key Objects | Cohomology groups (e.g., singular, de Rham, sheaf cohomology) | Torsion subgroups, torsion modules |
| Use in Topology | Computes invariants detecting holes, obstructions, characteristic classes | Identifies torsion phenomena in homology/cohomology, e.g., torsion coefficients |
| Examples | H^n(X, Z), de Rham cohomology groups H_{dR}^n(M) | Elements x with nx=0 in group G |
| Structure | Vector spaces or modules over rings, can include torsion components | Specifically finite order elements, substructure within larger groups |
| Relevance | Essential for distinguishing spaces beyond homology | Crucial for analyzing the fine structure of groups and cohomology groups |
Introduction to Cohomology and Torsion
Cohomology provides a powerful algebraic framework to study topological spaces by assigning algebraic invariants, revealing their global structures through cochain complexes and derived functors. Torsion elements in cohomology groups represent those nontrivial elements annihilated by some nonzero integer, quantifying obstructions and "twisted" features in the underlying topology. Understanding torsion in cohomology sheds light on finer geometric properties, including the presence of non-orientable structures and subtle invariants in manifold theory.
Fundamental Concepts in Cohomology
Cohomology studies algebraic invariants that classify topological spaces using cochain complexes and coboundary operators, capturing global geometric properties. Torsion in cohomology groups refers to elements of finite order, revealing subtle information about the space's structure, such as nontrivial cycles that vanish after multiplication by certain integers. Understanding the relationship between cohomology and torsion aids in distinguishing spaces with similar homology but different finer topological features.
Understanding Torsion in Algebraic Topology
Torsion in algebraic topology refers to elements of finite order in homology or cohomology groups, revealing subtle geometric and topological properties of spaces. Cohomology groups that contain torsion indicate the presence of nontrivial cycles that cannot be detected by ordinary homology alone, enriching the classification of topological spaces. Understanding torsion is essential for analyzing phenomena like fiber bundles and characteristic classes, where torsion reflects obstructions to certain topological constructions.
Key Differences Between Cohomology and Torsion
Cohomology is a mathematical tool used to study topological spaces by assigning algebraic invariants, capturing global structural properties through cohomology groups. Torsion refers to elements of finite order within these algebraic structures, often indicating subtle obstructions or symmetries in the topology. The key difference lies in cohomology providing a framework to analyze space structure, while torsion elements specifically reveal finite cyclic phenomena within that framework.
The Role of Torsion in Cohomology Groups
Torsion elements in cohomology groups reveal important structural information about topological spaces, reflecting phenomena such as non-trivial cycles that are not detected by homology over fields. These torsion components often arise in the cohomology of spaces with finite fundamental groups or in the presence of certain fiber bundles, influencing invariants like the cup product structure and spectral sequences. Understanding torsion in cohomology groups is crucial for classifying spaces, detecting subtle topological features, and connecting algebraic topology with arithmetic and geometric contexts.
Cohomological Torsion: Examples and Applications
Cohomological torsion appears as elements of finite order in the cohomology groups of topological spaces, revealing subtle geometric and algebraic structures. Classic examples include torsion in the integral cohomology of lens spaces and complex projective spaces with twisted coefficients, which play a crucial role in classifying fiber bundles and studying characteristic classes. Applications extend to algebraic geometry and number theory, where cohomological torsion informs the behavior of etale cohomology groups and the arithmetic of elliptic curves.
Cohomology vs Torsion: Mathematical Significance
Cohomology provides a framework for classifying and measuring topological spaces through algebraic invariants, revealing structures such as torsion elements in homology groups. Torsion components in cohomology groups indicate the presence of elements of finite order, which affect the space's properties and the behavior of maps between spaces. Understanding the interplay between cohomology and torsion is crucial in algebraic topology, algebraic geometry, and number theory for analyzing intricate topological and arithmetic phenomena.
Computation Techniques: Cohomology and Torsion
Computation techniques in cohomology involve the use of chain complexes and spectral sequences to systematically calculate cohomology groups, providing insights into topological spaces and algebraic structures. Torsion computation focuses on identifying elements of finite order within homology or cohomology groups, often utilizing tools such as exact sequences and universal coefficient theorems to isolate torsion subgroups. Advanced algorithms leverage these techniques to distinguish free components from torsion parts, enabling precise classification of algebraic invariants in various mathematical contexts.
Cohomology, Torsion, and Homological Algebra
Cohomology provides a powerful framework in homological algebra to study algebraic structures by associating sequences of abelian groups or modules that reveal topological and algebraic invariants. Torsion elements within these cohomology groups indicate finite order phenomena that are crucial for understanding obstructions and extensions in module theory and algebraic topology. The interplay between cohomology and torsion deepens insights into the structure of spaces and algebraic objects, enabling classification and analysis of complex algebraic invariants.
Conclusion: Cohomology and Torsion in Modern Mathematics
Cohomology provides a powerful framework in modern mathematics to analyze topological spaces by assigning algebraic invariants that reveal structural properties. Torsion elements, detected through cohomological methods, play a crucial role in understanding the finer aspects of these structures, particularly in algebraic topology and group theory. The interplay between cohomology and torsion deepens insights into geometric and algebraic phenomena, underpinning advancements in areas like algebraic geometry, number theory, and manifold theory.
Cohomology Infographic
 libterm.com
libterm.com