A polyhedral complex is a geometric structure formed by joining multiple polyhedra, ensuring their intersection is a face common to both. This concept is essential for understanding spaces in computational geometry and topology, where polyhedral complexes model shapes and surfaces with precise mathematical properties. Explore the rest of the article to discover how polyhedral complexes impact various fields and applications.
Table of Comparison
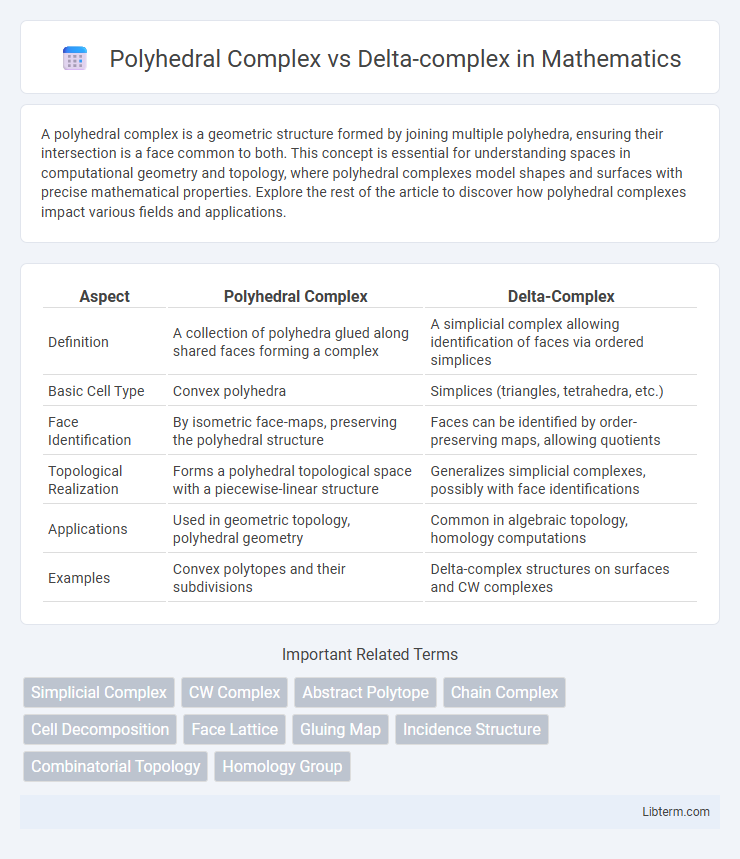
| Aspect | Polyhedral Complex | Delta-Complex |
|---|---|---|
| Definition | A collection of polyhedra glued along shared faces forming a complex | A simplicial complex allowing identification of faces via ordered simplices |
| Basic Cell Type | Convex polyhedra | Simplices (triangles, tetrahedra, etc.) |
| Face Identification | By isometric face-maps, preserving the polyhedral structure | Faces can be identified by order-preserving maps, allowing quotients |
| Topological Realization | Forms a polyhedral topological space with a piecewise-linear structure | Generalizes simplicial complexes, possibly with face identifications |
| Applications | Used in geometric topology, polyhedral geometry | Common in algebraic topology, homology computations |
| Examples | Convex polytopes and their subdivisions | Delta-complex structures on surfaces and CW complexes |
Introduction to Polyhedral Complexes and Delta-complexes
Polyhedral complexes generalize simplicial complexes by allowing polyhedra of various types to be glued together along shared faces, forming a structured topological space used in geometry and combinatorics. Delta-complexes, introduced by J.H.C. Whitehead, are a flexible framework for building spaces from simplices glued along faces with potentially multiple identifications, simplifying computations in algebraic topology. Understanding differences in cell structure and gluing maps between polyhedral and delta-complexes provides essential insights for applications in homology theory and geometric modeling.
Defining Polyhedral Complexes
Defining polyhedral complexes involves assembling convex polyhedra that intersect along shared faces, forming a finite collection closed under taking faces and intersections. Each polyhedron in the complex is typically embedded in Euclidean space, and the complex is characterized by properties such as dimension, finiteness, and face poset structure. Unlike Delta-complexes, which rely on simplices and face maps, polyhedral complexes allow for more general polytopes, enabling flexible geometric and combinatorial modeling in topology and combinatorics.
Understanding Delta-complexes
Delta-complexes provide a combinatorial framework to study topological spaces via simplices glued together along their faces, emphasizing the ordered structure of simplices and face maps. Unlike polyhedral complexes that allow gluing of general polyhedra, delta-complexes restrict to simplices with specified face identifications, facilitating the calculation of homology and cohomology through simplicial methods. The explicit face maps in delta-complexes enable algorithmic approaches in algebraic topology, making them essential tools for understanding singular homology and CW-complex structures.
Historical Development and Motivation
Polyhedral complexes originated as a generalization of simplicial complexes to study polyhedral shapes in topology and geometric combinatorics, providing flexibility in decomposing spaces into convex polytopes. Delta-complexes, introduced by J.H.C. Whitehead in the mid-20th century, aimed to simplify the combinatorial structure of spaces by allowing simplices to be glued together in a way that is less rigid than simplicial complexes but more structured than general CW complexes. The motivation behind both concepts was to develop effective tools for algebraic topology, with polyhedral complexes emphasizing geometric intuition and Delta-complexes focusing on combinatorial clarity and computational tractability.
Key Structural Differences
Polyhedral complexes consist of polyhedra assembled along shared faces, emphasizing strict intersection properties and allowing a rich geometric structure, whereas Delta-complexes rely on simplices glued via face maps with more flexible combinatorial rules. Polyhedral complexes support more general cell shapes beyond simplices, leading to varied dimensional cells and intricate face lattice arrangements, while Delta-complexes enforce a simplicial framework simplifying homological computations. The key structural difference lies in the rigidity of cell intersections in polyhedral complexes compared to the simplicial identifications in Delta-complexes, impacting their topological and combinatorial properties.
Methods of Construction
Polyhedral complexes are constructed by gluing together polyhedra along their faces using affine transformations that preserve the combinatorial and geometric structure, ensuring a well-defined cell complex. Delta-complexes are built from simplices by identifying faces via simplicial maps, emphasizing combinatorial properties and allowing more flexible gluings that do not necessarily preserve geometric embedding. The key difference lies in polyhedral complexes requiring rigid face identifications consistent with Euclidean geometry, whereas delta-complexes permit face identifications based solely on simplicial combinatorics.
Topological Properties Comparison
Polyhedral complexes exhibit a more general and flexible structure compared to delta-complexes, allowing cells to be arbitrary polytopes while delta-complexes restrict cells to simplices. Topologically, polyhedral complexes can model spaces with more intricate boundary identifications and accommodate non-simplicial cell gluings, leading to potentially richer homotopy types and more complex local connectivity properties. Delta-complexes, by relying on simplices, often provide simpler combinatorial models ideal for computational topology but may not capture certain topological nuances present in polyhedral decompositions.
Applications in Geometry and Topology
Polyhedral complexes provide a versatile framework for studying piecewise-linear structures in geometric topology, enabling precise cell decompositions that facilitate computations of homology and cohomology groups. Delta-complexes, defined using simplices glued along faces with relaxed gluing conditions, offer a combinatorial approach well-suited for handling fundamental group computations and simplicial homology in algebraic topology. Applications in geometry benefit from polyhedral complexes' ability to model polyhedral manifolds and orbifolds, while delta-complexes streamline the analysis of spaces with singularities or non-manifold structures through efficient simplicial approximations.
Advantages and Limitations
Polyhedral complexes provide a flexible framework for modeling geometric shapes with diverse polygonal cells, enabling efficient representation of complex topologies in computational geometry and algebraic topology. Delta-complexes simplify the structure by using simplices and allow for straightforward algebraic computations, but they lack the generality to represent shapes that require non-simplicial polytopes. Polyhedral complexes accommodate more general cell shapes, offering advantages in applications like mesh generation, while delta-complexes' limitations include less expressive power for modeling intricate polyhedral subdivisions.
Choosing Between Polyhedral Complexes and Delta-complexes
Choosing between polyhedral complexes and delta-complexes depends largely on the geometric and topological goals of a study. Polyhedral complexes offer flexibility for modeling spaces with general polyhedral shapes, making them ideal for applications requiring complex face structures and diverse cell shapes. Delta-complexes, characterized by simplicial decomposition, provide computational advantages and conceptual clarity when dealing with simplicial homology and fundamental category theories.
Polyhedral Complex Infographic
 libterm.com
libterm.com