A limit cycle is a closed trajectory in a dynamical system's phase space that solutions approach as time progresses, representing stable or unstable periodic behavior. These cycles are crucial in understanding oscillatory phenomena in fields such as biology, engineering, and physics. Explore the rest of this article to discover how limit cycles affect your system's long-term dynamics and stability.
Table of Comparison
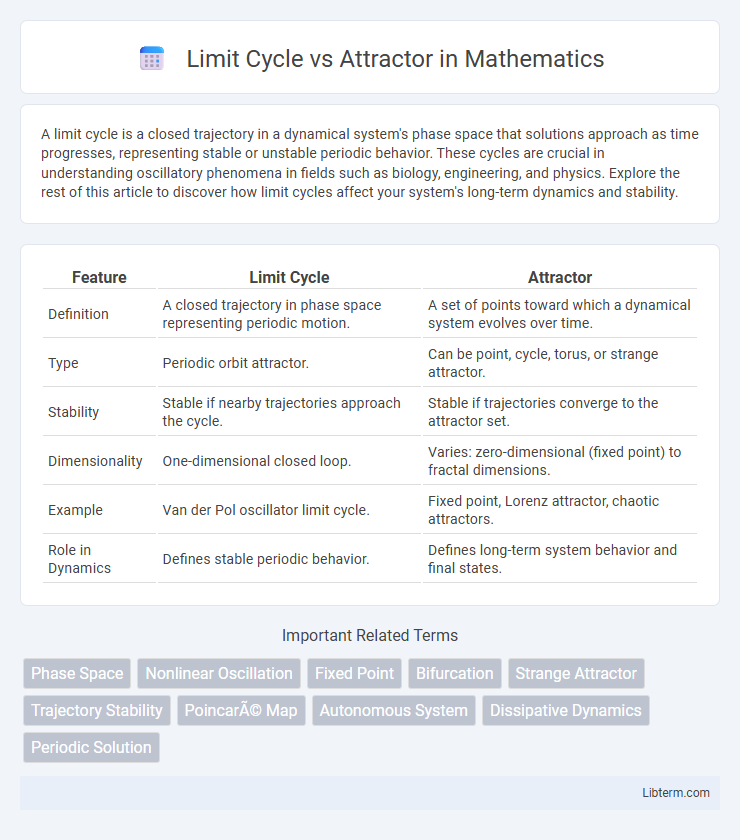
| Feature | Limit Cycle | Attractor |
|---|---|---|
| Definition | A closed trajectory in phase space representing periodic motion. | A set of points toward which a dynamical system evolves over time. |
| Type | Periodic orbit attractor. | Can be point, cycle, torus, or strange attractor. |
| Stability | Stable if nearby trajectories approach the cycle. | Stable if trajectories converge to the attractor set. |
| Dimensionality | One-dimensional closed loop. | Varies: zero-dimensional (fixed point) to fractal dimensions. |
| Example | Van der Pol oscillator limit cycle. | Fixed point, Lorenz attractor, chaotic attractors. |
| Role in Dynamics | Defines stable periodic behavior. | Defines long-term system behavior and final states. |
Introduction to Limit Cycles and Attractors
Limit cycles are closed trajectories in phase space representing periodic oscillations in nonlinear dynamical systems, acting as isolated stable or unstable solutions to differential equations. Attractors, including fixed points, limit cycles, or strange attractors, define the long-term behavior of a system where trajectories converge, revealing system stability and asymptotic states. Understanding limit cycles and attractors is essential for analyzing oscillatory phenomena and predicting system evolution in fields like physics, biology, and engineering.
Defining Limit Cycles in Dynamical Systems
Limit cycles in dynamical systems are closed trajectories representing periodic solutions where the system's behavior repeats over time. These cycles act as isolated closed orbits in the phase space, serving as attractors that other trajectories approach asymptotically. Unlike general attractors, limit cycles signify stable, sustained oscillations crucial in modeling biological rhythms, engineering controls, and nonlinear oscillators.
What is an Attractor? Key Characteristics
An attractor is a set of numerical values toward which a system tends to evolve, representing stable long-term behavior in dynamical systems. Key characteristics include its ability to draw trajectories from a wide range of initial conditions, stability under small perturbations, and the existence of fixed points, limit cycles, or strange attractors. Attractors serve as fundamental concepts for understanding patterns, predictability, and equilibrium states in nonlinear systems.
Mathematical Foundations: Limit Cycle vs Attractor
Limit cycles represent closed trajectories in phase space where a system's state oscillates indefinitely, characterized by their stability and periodicity in nonlinear dynamical systems. Attractors encompass a broader class of sets, including fixed points, limit cycles, and strange attractors, toward which system trajectories converge asymptotically. The mathematical foundation distinguishes limit cycles as isolated closed orbits with surrounding phase space trajectories converging or diverging, whereas attractors define invariant sets capturing long-term system behavior and stability.
Types of Attractors: Fixed Points, Limit Cycles, and Strange Attractors
Attractors in dynamical systems define the long-term behavior of trajectories, categorized as fixed points, limit cycles, and strange attractors. Fixed points represent stable equilibrium states where systems settle, while limit cycles correspond to closed trajectories indicating periodic oscillations. Strange attractors involve complex, fractal structures associated with chaotic systems, exhibiting sensitive dependence on initial conditions and non-repeating patterns.
Differences Between Limit Cycles and Other Attractors
Limit cycles are closed trajectories representing stable, periodic solutions in dynamical systems, whereas other attractors, such as fixed points or strange attractors, represent steady-state or chaotic behavior respectively. Unlike fixed points that converge to a single location in phase space, limit cycles maintain continuous oscillations with constant amplitude and period. Strange attractors exhibit sensitive dependence on initial conditions and complex fractal structures, contrasting the predictable repetitive nature of limit cycles.
Real-World Examples of Limit Cycles
Limit cycles represent stable, closed trajectories in nonlinear dynamical systems, seen in real-world examples like the regular beating of the human heart, the oscillations of a predator-prey population, and the rhythmic firing of neurons in the brain. These periodic solutions contrast with attractors, which may include fixed points, strange attractors, or limit cycles themselves, defining the long-term behavior of system states. Real-world limit cycles are crucial in understanding biological rhythms, mechanical vibrations, and electrical circuits where sustained oscillations occur without external periodic driving forces.
Real-World Examples of Attractors
Limit cycles represent closed trajectories in phase space where systems exhibit stable, repeated oscillations, commonly seen in biological rhythms like the heart's pacemaker or predator-prey population dynamics. Attractors encompass broader categories, including fixed points, limit cycles, and strange attractors, shaping real-world phenomena such as weather patterns in the Lorenz attractor or market movements in financial systems. Understanding attractors aids in predicting system stability and long-term behavior in fields ranging from engineering to ecology.
Practical Applications in Science and Engineering
Limit cycles serve as critical models for self-sustained oscillations in engineering systems such as electronic oscillators, biological rhythms, and mechanical vibrations, enabling precise control and prediction of periodic behaviors. Attractors, encompassing fixed points, limit cycles, and strange attractors, help in understanding the long-term behavior of dynamic systems across disciplines like climate modeling, robotics, and neural networks by describing how systems evolve over time to stable states or patterns. Practical applications leverage limit cycles for designing stable oscillatory circuits and controlling feedback loops, while attractors provide insights for stabilizing chaotic systems and optimizing system performance under varying conditions.
Summary: Limit Cycle vs Attractor – Key Takeaways
Limit cycles represent closed trajectories in phase space where systems exhibit periodic behavior, serving as specific examples of attractors that trap nearby trajectories. Attractors broadly encompass fixed points, limit cycles, and strange attractors, defining the long-term behavior of dynamic systems. Understanding the distinction aids in analyzing system stability and predicting oscillatory or steady-state outcomes.
Limit Cycle Infographic
 libterm.com
libterm.com