Linear algebra explores vector spaces, matrices, and linear transformations essential for solving systems of equations and understanding geometric properties. Mastery of these concepts unlocks applications in computer graphics, data science, and engineering, enhancing your problem-solving skills. Discover how linear algebra shapes various fields by reading the rest of the article.
Table of Comparison
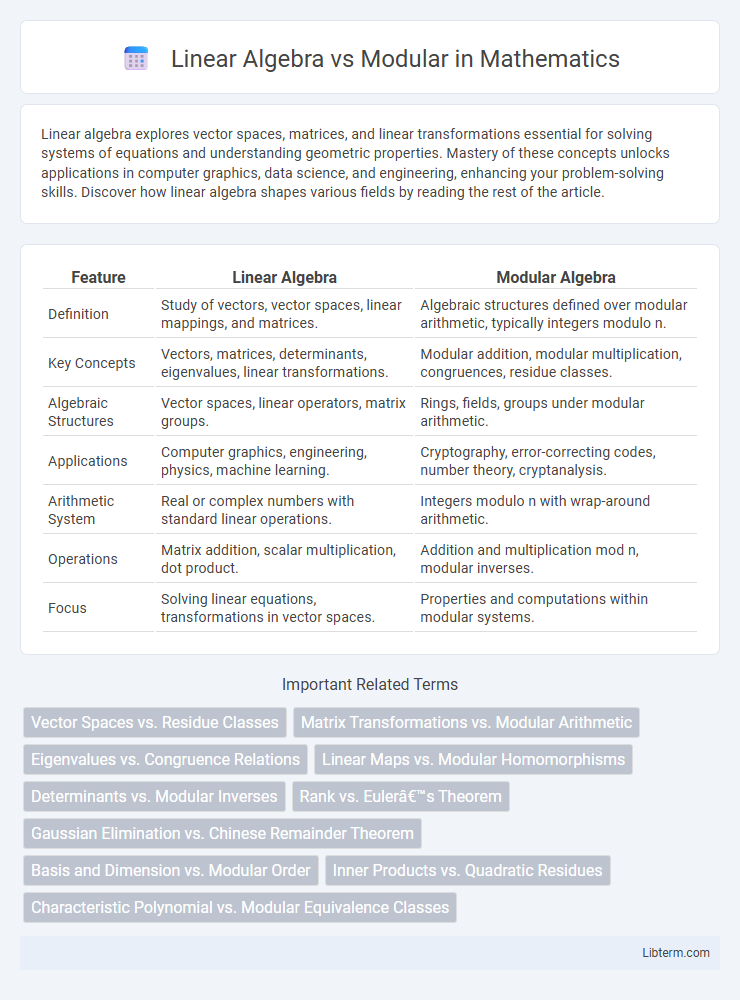
| Feature | Linear Algebra | Modular Algebra |
|---|---|---|
| Definition | Study of vectors, vector spaces, linear mappings, and matrices. | Algebraic structures defined over modular arithmetic, typically integers modulo n. |
| Key Concepts | Vectors, matrices, determinants, eigenvalues, linear transformations. | Modular addition, modular multiplication, congruences, residue classes. |
| Algebraic Structures | Vector spaces, linear operators, matrix groups. | Rings, fields, groups under modular arithmetic. |
| Applications | Computer graphics, engineering, physics, machine learning. | Cryptography, error-correcting codes, number theory, cryptanalysis. |
| Arithmetic System | Real or complex numbers with standard linear operations. | Integers modulo n with wrap-around arithmetic. |
| Operations | Matrix addition, scalar multiplication, dot product. | Addition and multiplication mod n, modular inverses. |
| Focus | Solving linear equations, transformations in vector spaces. | Properties and computations within modular systems. |
Introduction to Linear Algebra and Modular Arithmetic
Linear Algebra focuses on vector spaces, linear mappings, matrices, and systems of linear equations, providing foundational tools for solving multidimensional problems. Modular Arithmetic deals with integers and congruences within a fixed modulus, essential for cryptography, number theory, and computer science applications. Both fields emphasize algebraic structures but differ in scope: Linear Algebra centers on continuous spaces, while Modular Arithmetic operates within discrete modular systems.
Fundamental Concepts: Vectors vs Congruence
Linear algebra centers on vectors, which are objects defined by magnitude and direction within vector spaces, allowing operations such as addition and scalar multiplication. Modular arithmetic, however, revolves around congruence relations, where numbers are equivalent under a fixed modulus, forming equivalence classes that enable computations in finite rings or fields. Understanding vectors facilitates geometric interpretations and transformations, while congruence provides a foundation for solving number theory problems and cryptographic algorithms.
Key Operations in Linear Algebra
Linear algebra centers on key operations such as matrix multiplication, vector addition, scalar multiplication, and finding determinants, eigenvalues, and eigenvectors crucial for solving linear systems and transformations. Modular arithmetic, by contrast, emphasizes operations like addition, subtraction, multiplication, and inversion within a finite set defined by a modulus, impacting cryptography and number theory. While both deal with algebraic structures, the complexity and application of linear algebra's matrix-based operations differentiate it significantly from modular arithmetic's residue calculations.
Essential Operations in Modular Arithmetic
Essential operations in modular arithmetic include addition, subtraction, multiplication, and finding modular inverses, all performed with respect to a fixed modulus. Unlike linear algebra, which operates over fields or vector spaces with real or complex numbers, modular arithmetic confines results within a finite set of integers, enabling cyclic properties and congruences crucial for cryptography and number theory. Efficient algorithms for modular exponentiation and modular inversion underpin secure communication protocols and error-correcting codes in computational applications.
Applications of Linear Algebra
Linear algebra is widely applied in computer graphics, machine learning, and engineering for solving systems of linear equations, vector space transformations, and matrix computations essential for modeling and simulations. Modular algebra, on the other hand, focuses on arithmetic operations within a finite set, playing a crucial role in cryptography, coding theory, and error detection. The applications of linear algebra often leverage its ability to handle continuous data and large-scale numerical computations, distinguishing it from modular algebra's discrete and finite structures.
Applications of Modular Arithmetic
Modular arithmetic plays a crucial role in cryptography, enabling secure communication through algorithms like RSA and Diffie-Hellman. It is essential for computer science applications such as hashing, error detection, and digital signal processing. Unlike linear algebra, which focuses on vector spaces and matrix computations, modular arithmetic emphasizes residue classes and cyclical patterns for problem-solving in discrete mathematics and number theory.
Comparing Structures: Fields, Rings, and Spaces
Linear algebra primarily deals with vector spaces over fields such as the real or complex numbers, where operations like addition and scalar multiplication satisfy specific axioms ensuring closure, associativity, and distributivity. Modular arithmetic, often studied within ring theory, involves structures called rings where addition and multiplication are defined modulo a fixed integer, typically lacking multiplicative inverses for all elements, distinguishing them from fields. Comparing these structures reveals that vector spaces require underlying fields for scalar multiplication, whereas modules generalize this concept by allowing scalars from rings, highlighting fundamental differences in linear transformations and solvability of linear systems.
Solving Equations: Techniques and Challenges
Linear algebra techniques for solving equations involve matrix operations, determinants, and vector spaces, enabling efficient solutions for systems with real or complex coefficients. Modular arithmetic equations introduce challenges such as non-invertible elements and require specialized algorithms like the Chinese Remainder Theorem and modular inverses to handle congruences. Addressing modular systems often involves combinatorial and number-theoretic methods distinct from linear algebra's continuous frameworks.
Real-World Use Cases: Engineering, Cryptography, and Beyond
Linear algebra underpins engineering applications such as structural analysis, control systems, and computer graphics, enabling precise modeling of real-world phenomena using vectors and matrices. Modular arithmetic is foundational in cryptography, securing digital communication through algorithms like RSA and ECC that rely on computations within finite fields. Both mathematical frameworks extend their utility beyond these areas, influencing error detection, coding theory, and optimization problems in diverse technological fields.
Summary: Choosing Between Linear Algebra and Modular Arithmetic
Linear Algebra deals with vector spaces and linear mappings, essential for solving systems of linear equations and transformations in fields like engineering and computer science. Modular Arithmetic focuses on integers with equivalence classes modulo a number, crucial in cryptography, number theory, and coding theory. Selecting between them depends on the problem domain: Linear Algebra suits continuous data and multidimensional analysis, while Modular Arithmetic excels in discrete systems and encryption algorithms.
Linear Algebra Infographic
 libterm.com
libterm.com