Singular measure refers to a mathematical concept used to describe measures that assign positive weight to sets of zero Lebesgue measure, often contrasting with absolutely continuous measures. These measures play a crucial role in fields such as fractal geometry and probability theory, helping to analyze distributions that are concentrated on lower-dimensional subsets. Explore the rest of the article to understand how singular measures impact various applications and the underlying theory.
Table of Comparison
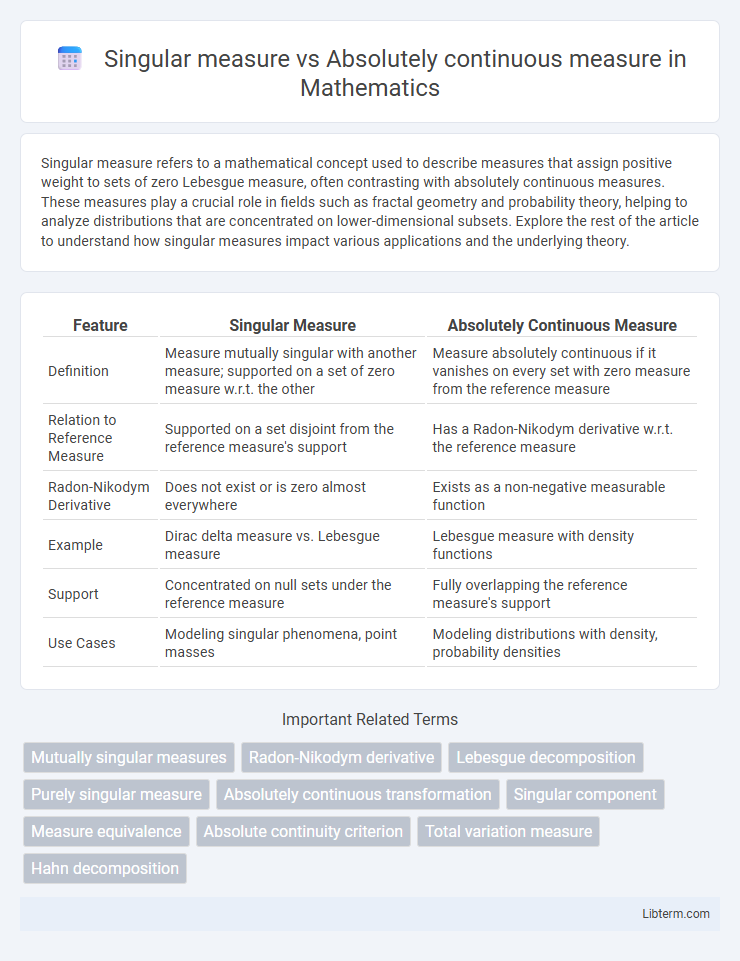
| Feature | Singular Measure | Absolutely Continuous Measure |
|---|---|---|
| Definition | Measure mutually singular with another measure; supported on a set of zero measure w.r.t. the other | Measure absolutely continuous if it vanishes on every set with zero measure from the reference measure |
| Relation to Reference Measure | Supported on a set disjoint from the reference measure's support | Has a Radon-Nikodym derivative w.r.t. the reference measure |
| Radon-Nikodym Derivative | Does not exist or is zero almost everywhere | Exists as a non-negative measurable function |
| Example | Dirac delta measure vs. Lebesgue measure | Lebesgue measure with density functions |
| Support | Concentrated on null sets under the reference measure | Fully overlapping the reference measure's support |
| Use Cases | Modeling singular phenomena, point masses | Modeling distributions with density, probability densities |
Understanding Measure Theory: A Brief Overview
Singular measures and absolutely continuous measures are fundamental concepts in measure theory used to classify measures based on their relationship with a reference measure, typically the Lebesgue measure. Singular measures assign full measure to sets where the reference measure is zero, meaning they are concentrated on a set of Lebesgue measure zero, whereas absolutely continuous measures have a density with respect to the reference measure, allowing representation via the Radon-Nikodym derivative. Understanding these distinctions enables deeper insights into decomposition theorems like the Lebesgue decomposition, essential for advanced integration and probability theory.
Defining Singular Measures
Singular measures are defined as measures supported on sets of Lebesgue measure zero, making them mutually singular with respect to absolutely continuous measures. These measures assign full measure to subsets where absolutely continuous measures vanish, leading to no overlap in their mass distribution. Understanding singular measures is crucial in the Lebesgue decomposition theorem, which separates any measure into absolutely continuous and singular parts relative to a reference measure.
What Are Absolutely Continuous Measures?
Absolutely continuous measures are defined by their relationship to a reference measure, typically the Lebesgue measure, where the measure of any set is zero if the reference measure of that set is zero. This property ensures the existence of a Radon-Nikodym derivative, which serves as a density function that relates the absolutely continuous measure to the reference measure. In contrast to singular measures that assign measure to sets disjoint from the support of the reference measure, absolutely continuous measures share the same null sets as the reference measure and have no singular component.
Key Differences Between Singular and Absolutely Continuous Measures
Singular measures and absolutely continuous measures differ primarily in their relationship to a reference measure, often the Lebesgue measure. An absolutely continuous measure has a density function with respect to the reference measure, meaning it assigns zero measure to sets of zero reference measure, while a singular measure is supported on a set of zero reference measure, making it mutually singular. Key differences include absolute continuity implying the existence of a Radon-Nikodym derivative, whereas singularity involves disjoint support, highlighting fundamentally distinct ways measures relate to the underlying space.
Mathematical Formalism: Singular Measure Explained
A singular measure m with respect to another measure n on a measurable space (X, S) is defined by the existence of two disjoint measurable sets A and B such that X = A B, m is concentrated on A (m(B) = 0), and n is concentrated on B (n(A) = 0). This orthogonality condition implies that the Lebesgue decomposition theorem expresses any measure as the sum of an absolutely continuous measure and a singular measure relative to n. Singular measures often arise in fractal geometry and measure theory, exemplified by the Cantor measure, which is singular with respect to the Lebesgue measure.
Mathematical Formalism: Absolutely Continuous Measure Explained
An absolutely continuous measure m with respect to another measure n on a measurable space (X, S) satisfies the Radon-Nikodym theorem, which guarantees the existence of a measurable function f such that m(A) = _A f dn for all A in S. This function f, known as the Radon-Nikodym derivative, provides a density of m with respect to n, making absolutely continuous measures characterized by their lack of singular parts. In contrast, a singular measure is supported on a set of n-measure zero, making the decomposition m = m_ac + m_s, where m_ac is absolutely continuous and m_s is singular, fundamental in measure theory.
The Radon-Nikodym Theorem and Its Role
The Radon-Nikodym theorem provides a vital tool for distinguishing between singular measures, which are mutually singular with respect to a reference measure, and absolutely continuous measures that admit density functions with respect to that measure. By enabling the representation of an absolutely continuous measure as an integral of a Radon-Nikodym derivative (or density) relative to another measure, the theorem clarifies the structure and relationships of measures in measure theory. This fundamental result underpins numerous applications in probability, ergodic theory, and functional analysis, where understanding the decomposition of measures into singular and absolutely continuous parts is essential.
Examples Illustrating Singular and Absolutely Continuous Measures
A classical example of a singular measure is the Cantor measure, which is supported on the Cantor set and assigns measure zero to any interval, demonstrating its singularity with respect to Lebesgue measure. In contrast, the Lebesgue measure itself serves as a prime example of an absolutely continuous measure, as it can be expressed as the integral of its density function with respect to itself. Another illustrative case is the distribution of a random variable with an absolutely continuous probability density function versus the distribution concentrated on a fractal subset, highlighting the conceptual distinction between singular and absolutely continuous measures.
Applications in Probability and Real Analysis
Singular measures are used in probability to model distributions concentrated on sets of Lebesgue measure zero, such as Cantor-type distributions, which are crucial in fractal geometry and stochastic processes with irregular paths. Absolutely continuous measures, defined via Radon-Nikodym derivatives with respect to Lebesgue measure, underpin classical probability density functions and enable the use of differential calculus in real analysis for evaluating integrals and solving differential equations. The distinction between these measures influences the decomposition of complex measures into mutually singular and absolutely continuous parts, impacting convergence theorems and ergodic theory applications.
Conclusion: Choosing the Appropriate Measure
Choosing between a singular measure and an absolutely continuous measure depends on the nature of the underlying data and the required analytical precision. Singular measures are ideal for modeling phenomena with discrete or fractal-like support, whereas absolutely continuous measures suit settings with smooth density functions relative to a reference measure, typically the Lebesgue measure. Proper selection enhances mathematical modeling accuracy and ensures appropriate interpretation in applications such as probability theory and functional analysis.
Singular measure Infographic
 libterm.com
libterm.com