Limits define the value a function approaches as the input nears a specific point, playing a crucial role in calculus and mathematical analysis. Understanding limits helps you analyze function behavior, continuity, and the foundation of derivatives. Explore the article to deepen your grasp of limits and their applications in solving complex problems.
Table of Comparison
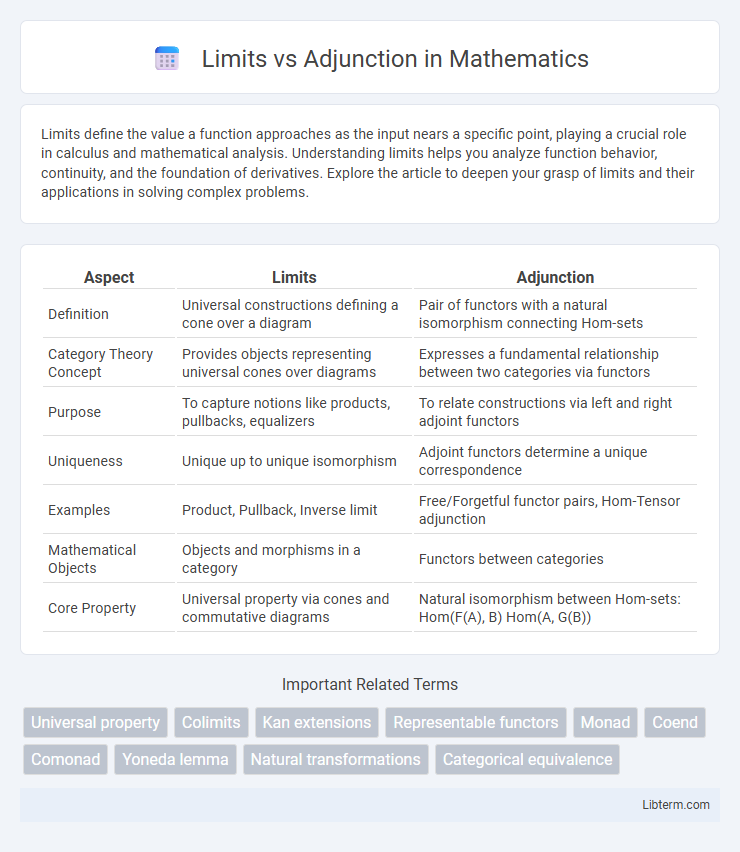
| Aspect | Limits | Adjunction |
|---|---|---|
| Definition | Universal constructions defining a cone over a diagram | Pair of functors with a natural isomorphism connecting Hom-sets |
| Category Theory Concept | Provides objects representing universal cones over diagrams | Expresses a fundamental relationship between two categories via functors |
| Purpose | To capture notions like products, pullbacks, equalizers | To relate constructions via left and right adjoint functors |
| Uniqueness | Unique up to unique isomorphism | Adjoint functors determine a unique correspondence |
| Examples | Product, Pullback, Inverse limit | Free/Forgetful functor pairs, Hom-Tensor adjunction |
| Mathematical Objects | Objects and morphisms in a category | Functors between categories |
| Core Property | Universal property via cones and commutative diagrams | Natural isomorphism between Hom-sets: Hom(F(A), B) Hom(A, G(B)) |
Introduction to Limits and Adjunctions
Limits in category theory represent universal constructions that capture the essence of diagrams by providing a single object embodying their collective structural properties. Adjunctions describe pairs of functors that establish a fundamental relationship between categories, characterized by a natural isomorphism between hom-sets, reflecting maximum compatibility. Understanding these concepts lays the groundwork for interpreting complex categorical relationships and universal properties in mathematical structures.
Fundamental Concepts in Category Theory
Limits in category theory represent universal cones that capture the notion of objects acting as optimal solutions to diagram completion problems, essential for understanding product, pullback, and inverse limit constructions. Adjunctions formalize a pair of functors connecting two categories with a natural isomorphism between hom-sets, reflecting an intrinsic correspondence between constructions like free/forgetful functors or limits/colimits. Understanding the interplay between limits and adjunctions reveals fundamental structural insights, such as how right adjoints preserve limits and how universal properties underpin categorical equivalences and dualities.
Defining Limits: Meaning and Examples
Limits in category theory provide a universal way to capture the notion of converging structures by associating a single object to a diagram of objects and morphisms. A limit of a diagram is an object equipped with morphisms to each object in the diagram that uniquely factorizes any other such cone, exemplified by products and pullbacks. This concept formalizes how complex constructions like inverse limits and equalizers unify diverse mathematical contexts under a universal property framework.
Understanding Adjunction: Overview and Intuition
Adjunction in category theory describes a pair of functors that establish a natural correspondence between morphisms, capturing a deep relationship between structures across different categories. This concept contrasts with limits, which focus on universal cones characterizing objects through their relationships with a diagram, whereas adjunctions highlight how a functor can 'reverse' or 'undo' another functor's action in a structured way. Understanding adjunctions involves grasping the intuitive notion of optimality and universality behind these morphism correspondences, providing a powerful framework for relating mathematical constructs and enabling constructions such as free objects and reflective subcategories.
Key Differences: Limits vs Adjunction
Limits in category theory represent universal constructions that capture the notion of a universal cone over a diagram, assembling objects and morphisms into a universal solution defined by their universal property. Adjunctions describe a pair of functors between categories that stand in a specific relationship characterized by natural isomorphisms between hom-sets, encapsulating the concept of a best approximate inverse. The key difference lies in limits addressing the existence of universal objects satisfying specific diagrams, whereas adjunctions focus on a duality relationship between two functors expressed via unit and counit natural transformations.
Relationships Between Limits and Adjunctions
Limits in category theory often arise as special cases of adjunctions, where the limit functor serves as a right adjoint to a diagonal functor. This adjoint relationship characterizes limits by universal properties that preserve the structure of cones and diagrams within categories. Understanding the interplay between limits and adjunctions reveals how universal constructions and natural transformations are interconnected through categorical frameworks.
Applications of Limits in Mathematics
Limits play a crucial role in various branches of mathematics such as calculus, real analysis, and topology by providing a foundational framework for defining continuity, derivatives, and integrals. In category theory, limits enable the construction of universal objects that unify diagrams, facilitating the study of complex structures and functors. Applications of limits extend to solving systems of equations, analyzing convergence in sequences and series, and modeling dynamic systems in mathematical physics and engineering.
Applications of Adjunctions in Mathematics
Adjunctions play a crucial role in various branches of mathematics by providing a systematic way to compare and construct objects across different categories, facilitating the understanding of limits, colimits, and universal properties. They are instrumental in algebraic topology for constructing homology and cohomology theories, enabling the translation of geometric information into algebraic data. In category theory, adjunctions underpin the theory of monads and comonads, which are essential in the study of algebraic structures and computational semantics.
Limits and Adjunctions in Various Categories
Limits in category theory provide a universal way to capture the structure of diagrams by specifying cones that factor uniquely through the limit object, applicable across categories like Set, Top, and Ab. Adjunctions formalize pairs of functors between categories that establish a precise correspondence between hom-sets, linking constructions such as free and forgetful functors in algebraic contexts. The interplay between limits and adjunctions reveals that right adjoints preserve limits while left adjoints preserve colimits, emphasizing their fundamental role in structuring categorical relationships.
Conclusion: Choosing Between Limits and Adjunctions
Limits and adjunctions serve distinct roles in category theory, with limits capturing universal properties related to cones and diagrams, while adjunctions characterize pairs of functors linked by natural transformations. Selecting between limits and adjunctions depends on the structural requirements of a problem: limits provide solutions to universal constructions within a category, whereas adjunctions reveal deeper relationships between categories through functorial correspondences. Understanding these differences guides mathematicians in applying the appropriate tool for constructing objects or establishing equivalences in complex categorical frameworks.
Limits Infographic
 libterm.com
libterm.com