A strongly compact cardinal is a type of large cardinal in set theory characterized by its ability to extend certain compactness properties to infinitary languages, making it stronger than measurable cardinals. These cardinals have crucial implications in the study of model theory and the foundations of mathematics due to their high consistency strength and their role in controlling the behavior of ultrafilters and elementary embeddings. Explore the rest of the article to understand the deep significance and applications of strongly compact cardinals in modern set theory.
Table of Comparison
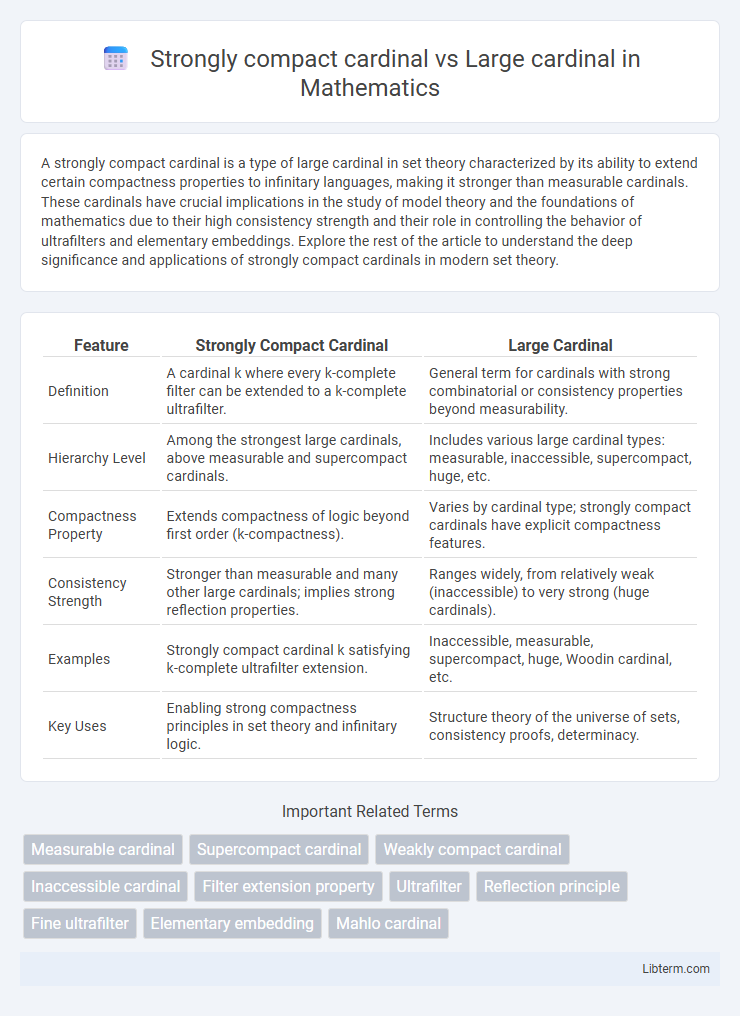
| Feature | Strongly Compact Cardinal | Large Cardinal |
|---|---|---|
| Definition | A cardinal k where every k-complete filter can be extended to a k-complete ultrafilter. | General term for cardinals with strong combinatorial or consistency properties beyond measurability. |
| Hierarchy Level | Among the strongest large cardinals, above measurable and supercompact cardinals. | Includes various large cardinal types: measurable, inaccessible, supercompact, huge, etc. |
| Compactness Property | Extends compactness of logic beyond first order (k-compactness). | Varies by cardinal type; strongly compact cardinals have explicit compactness features. |
| Consistency Strength | Stronger than measurable and many other large cardinals; implies strong reflection properties. | Ranges widely, from relatively weak (inaccessible) to very strong (huge cardinals). |
| Examples | Strongly compact cardinal k satisfying k-complete ultrafilter extension. | Inaccessible, measurable, supercompact, huge, Woodin cardinal, etc. |
| Key Uses | Enabling strong compactness principles in set theory and infinitary logic. | Structure theory of the universe of sets, consistency proofs, determinacy. |
Introduction to Large Cardinals
Large cardinals are a pivotal concept in set theory, representing infinite sizes with extraordinary combinatorial properties that extend beyond the standard hierarchy of infinities. Strongly compact cardinals are a significant subclass of large cardinals characterized by strong compactness properties related to ultrafilters and model theory, providing extensive reflection principles and consistency strength. Understanding strongly compact cardinals helps illuminate the broader landscape of large cardinal axioms, which shape the foundations of mathematics by influencing the structure and behavior of the set-theoretic universe.
Defining Strongly Compact Cardinals
Strongly compact cardinals are a type of large cardinal characterized by the extension of the compactness property from first-order logic to infinitary logics, meaning every k-complete filter can be extended to a k-complete ultrafilter. In set theory, a cardinal k is strongly compact if for every set S and every k-complete filter on S, there exists a k-complete ultrafilter extending it, reflecting a profound level of largeness and consistency strength. These cardinals are pivotal in exploring the hierarchy of large cardinals, sitting above measurable cardinals and having strong implications in models of set theory and infinitary combinatorics.
The Hierarchy of Large Cardinals
Strongly compact cardinals rank high in the hierarchy of large cardinals due to their powerful compactness properties extending beyond measurable cardinals. This hierarchy progresses from inaccessible and measurable cardinals to supercompact and extendible cardinals, with strongly compact cardinals positioned above measurable but below supercompact cardinals. Understanding their role illuminates the intricate structure of large cardinal axioms and their impact on set theory and consistency strength.
Key Properties of Strongly Compact Cardinals
Strongly compact cardinals are large cardinals characterized by their ability to extend compactness principles from logic to higher infinities, ensuring every k-complete filter can be extended to a k-complete ultrafilter. They exhibit immense combinatorial strength, surpassing measurable cardinals by enforcing strong compactness in infinitary languages and impacting the structure of the universe of sets. Their key properties include the existence of k-complete ultrafilters, preservation of compactness for infinitary languages L_k,l, and manifestation of strong reflection principles.
Comparison: Strongly Compact vs Other Large Cardinals
Strongly compact cardinals are a significant type of large cardinal characterized by the strong compactness property, which ensures that every k-complete filter extends to a k-complete ultrafilter. They are stronger than measurable cardinals, as every strongly compact cardinal is measurable, but not every measurable cardinal is strongly compact. Compared to supercompact cardinals, strongly compact cardinals have a weaker embedding characterization, with supercompact cardinals exhibiting higher consistency strength and more extensive combinatorial properties.
Consistency Strength and Implications
Strongly compact cardinals possess higher consistency strength than many large cardinals, such as measurable cardinals, due to their ability to compactify infinitary logic with lambda-sized sets. Their consistency implies the existence of numerous large cardinals, establishing them as a benchmark in the hierarchy of large cardinal axioms within set theory. The strong compactness property leads to profound implications in model theory, impacting the understanding of filter extensions and ultrafilters beyond the scope of weaker large cardinal notions.
Applications in Set Theory
Strongly compact cardinals are a specific type of large cardinal with profound applications in set theory, particularly in the study of infinitary combinatorics and model theory. Their characterization by the existence of fine, k-complete ultrafilters enables the extension of compactness arguments beyond first-order logic, facilitating generalized compactness theorems and impacting the structure of the universe of sets. Large cardinals, encompassing a hierarchy including measurable, supercompact, and strongly compact cardinals, provide critical tools for understanding consistency strengths, independence results, and the fine structure of models in set theory.
Notable Theorems Involving Strongly Compact Cardinals
Strongly compact cardinals are a profound subclass within the large cardinal hierarchy characterized by their strong compactness property, which ensures the existence of elementary embeddings with critical points and measures extending to all sets of smaller cardinality. Notable theorems include Ketonen's theorem on the equivalence between strong compactness and the existence of fine, normal ultrafilters on certain set-theoretic structures, and Magidor's results showing that strongly compact cardinals imply the strong tree property and have deep implications for combinatorial set theory. These theorems emphasize the pivotal role of strongly compact cardinals in connecting large cardinals with fine structural and combinatorial principles in set theory.
Open Questions and Research Directions
Strongly compact cardinals, a pivotal concept within large cardinal hierarchy, exhibit profound connections to model theory and infinitary combinatorics, yet several open questions persist regarding their exact consistency strength relative to other large cardinal axioms. Research continues to investigate whether strongly compact cardinals can exist without measurable cardinals below them and explores their implications for the structure of the set-theoretic universe, particularly in the context of forcing and inner model theory. Advances in these directions aim to clarify the boundaries between strong compactness, supercompactness, and other large cardinal properties, enhancing understanding of their role in the foundations of mathematics.
Conclusion: The Role of Strongly Compact Cardinals in Mathematics
Strongly compact cardinals represent a crucial subclass of large cardinals, characterized by their profound impact on set theory and model theory through the compactness property for infinitary languages. Their existence implies significant consistency strength, surpassing measurable cardinals, and they facilitate the extension of classical compactness results beyond first-order logic. Strongly compact cardinals serve as foundational tools in understanding the structure of the universe of sets, influencing areas such as forcing, inner model theory, and the formulation of higher-order logic.
Strongly compact cardinal Infographic
 libterm.com
libterm.com