Superharmonic functions play a crucial role in potential theory and mathematical analysis, characterized by their property of being greater than or equal to their mean values over certain regions. These functions are instrumental in solving partial differential equations and modeling physical phenomena such as electrostatics and fluid flow. Explore the article to understand how superharmonic functions impact your work in mathematics and applied sciences.
Table of Comparison
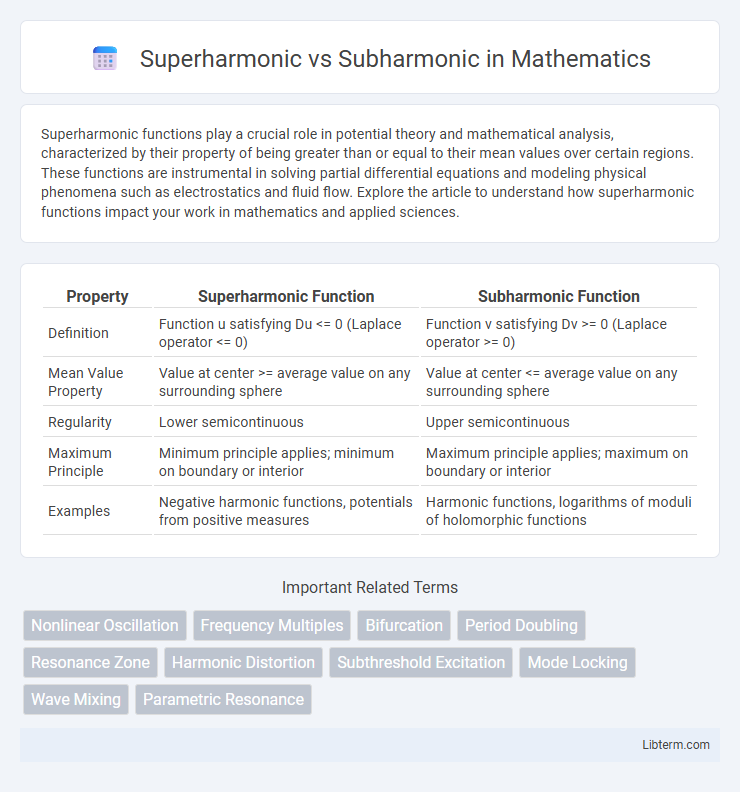
| Property | Superharmonic Function | Subharmonic Function |
|---|---|---|
| Definition | Function u satisfying Du <= 0 (Laplace operator <= 0) | Function v satisfying Dv >= 0 (Laplace operator >= 0) |
| Mean Value Property | Value at center >= average value on any surrounding sphere | Value at center <= average value on any surrounding sphere |
| Regularity | Lower semicontinuous | Upper semicontinuous |
| Maximum Principle | Minimum principle applies; minimum on boundary or interior | Maximum principle applies; maximum on boundary or interior |
| Examples | Negative harmonic functions, potentials from positive measures | Harmonic functions, logarithms of moduli of holomorphic functions |
Introduction to Harmonics
Harmonics are integral multiples of a fundamental frequency, shaping sound and signal characteristics in various fields such as acoustics, electronics, and vibration analysis. Superharmonics refer to frequencies above the fundamental that are integer multiples, while subharmonics are frequencies below the fundamental, often fractional divisions of it. Understanding the distinction between superharmonic and subharmonic frequencies is crucial for analyzing signal behavior, system resonance, and controlling unwanted vibrations or distortions.
Defining Superharmonic Frequencies
Superharmonic frequencies are integer multiples of a fundamental frequency, representing higher frequency components within a harmonic series. These frequencies arise in various physical and engineering contexts, such as signal processing and acoustics, where they contribute to the timbre and richness of sounds. Understanding superharmonic frequencies is essential for analyzing waveforms, designing filters, and enhancing audio synthesis techniques.
Understanding Subharmonic Frequencies
Subharmonic frequencies occur at fractional intervals of a fundamental frequency, typically at integer divisions such as half or one-third of the original frequency, distinguishing them from superharmonics, which are multiples above the fundamental frequency. These subharmonics often arise in nonlinear systems where energy redistributes into lower-frequency components, impacting signal analysis and acoustic applications. Understanding subharmonic generation aids in fields like vibration analysis, structural health monitoring, and nonlinear dynamics by revealing hidden resonances and instability mechanisms.
Key Differences: Superharmonics vs Subharmonics
Superharmonics are frequencies that are integer multiples of a fundamental frequency, occurring above the fundamental, while subharmonics are fractional frequencies appearing below the fundamental frequency. Superharmonics typically arise in power systems due to non-linear loads, causing distortions at higher frequencies, whereas subharmonics often result from system instabilities or oscillations at frequencies below the main signal. Understanding these distinctions is critical for diagnosing and mitigating harmonic distortions in electrical power quality analysis.
Generation of Superharmonic Waves
Superharmonic waves are generated when a fundamental frequency undergoes nonlinear distortion, producing frequencies that are integer multiples of the original signal such as 2x, 3x, or higher harmonics. In contrast, subharmonic waves appear at fractional frequencies of the fundamental frequency, like half or one-third of the original frequency. The generation of superharmonic waves is critical in fields like nonlinear acoustics, vibration analysis, and ultrasonic imaging, where the amplification of higher-order harmonics enhances signal resolution and material characterization.
Formation of Subharmonic Waves
Subharmonic waves form through nonlinear processes in systems driven at fundamental frequencies, where energy transfers to frequencies at integer fractions of the original. These waves typically emerge in fluid dynamics and acoustics when instabilities cause oscillations at half or one-third the driving frequency, differing from superharmonics that appear at multiples. The formation involves parametric resonance, allowing subharmonic modes to amplify and sustain energy at submultiples of the initial excitation.
Applications of Superharmonics in Technology
Superharmonics, generated at integer multiples of a fundamental frequency, are widely used in advanced signal processing applications such as high-resolution spectroscopy, ultrasound imaging, and nonlinear optics. In power systems, superharmonic frequencies facilitate the identification and mitigation of electromagnetic interference, enhancing grid stability and efficiency. These frequencies also play a critical role in harmonic filtering and improving the performance of RF communication devices by enabling precise frequency control and signal modulation.
Practical Uses of Subharmonics
Subharmonics, frequencies at fractions of a fundamental frequency, play a crucial role in practical applications such as vibration analysis, structural health monitoring, and nonlinear acoustics. Their detection helps identify hidden faults in rotating machinery and materials, providing early warnings to prevent catastrophic failures. This makes subharmonics valuable in industrial maintenance, aerospace engineering, and medical ultrasound technologies.
Challenges in Analyzing Harmonic Components
Analyzing superharmonic and subharmonic components presents challenges due to their frequency overlap with fundamental and noise signals, complicating precise identification in signal processing. The nonlinear behavior in systems producing these harmonics introduces spectral spreading and amplitude modulation, making isolation and quantification difficult. Advanced filtering techniques and high-resolution spectral analysis are essential to accurately distinguish superharmonic and subharmonic frequencies for reliable diagnostics and control in engineering applications.
Future Trends in Harmonic Research
Future trends in harmonic research emphasize advanced superharmonic and subharmonic generation techniques using nonlinear optical materials and engineered metamaterials, enabling precise frequency control for high-resolution imaging and signal processing. Emerging applications include enhanced ultrasound imaging, quantum communication channels, and efficient energy conversion systems by exploiting controlled spectral content at higher-order harmonics. Integration of machine learning algorithms to optimize harmonic wave generation patterns promises significant improvements in real-time diagnostics and adaptive acoustic environments.
Superharmonic Infographic
 libterm.com
libterm.com