Automorphic forms are complex-valued functions defined on the upper half-plane that remain invariant under the action of discrete groups, playing a crucial role in number theory and representation theory. These forms generalize periodic functions and connect deep mathematical fields such as modular forms, L-functions, and arithmetic geometry. Explore the rest of the article to uncover how automorphic forms influence modern mathematics and Your understanding of symmetry.
Table of Comparison
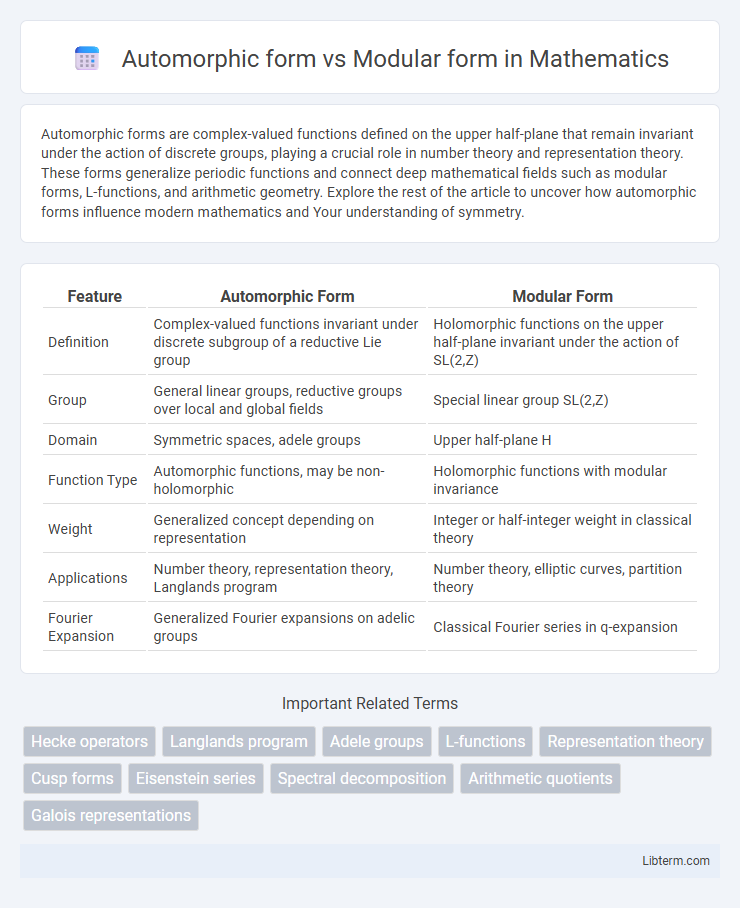
| Feature | Automorphic Form | Modular Form |
|---|---|---|
| Definition | Complex-valued functions invariant under discrete subgroup of a reductive Lie group | Holomorphic functions on the upper half-plane invariant under the action of SL(2,Z) |
| Group | General linear groups, reductive groups over local and global fields | Special linear group SL(2,Z) |
| Domain | Symmetric spaces, adele groups | Upper half-plane H |
| Function Type | Automorphic functions, may be non-holomorphic | Holomorphic functions with modular invariance |
| Weight | Generalized concept depending on representation | Integer or half-integer weight in classical theory |
| Applications | Number theory, representation theory, Langlands program | Number theory, elliptic curves, partition theory |
| Fourier Expansion | Generalized Fourier expansions on adelic groups | Classical Fourier series in q-expansion |
Introduction to Automorphic and Modular Forms
Automorphic forms generalize modular forms by allowing transformations under more general discrete subgroups of Lie groups beyond SL(2,Z). Modular forms are holomorphic functions on the complex upper half-plane that exhibit specific transformation properties under the modular group and play a central role in number theory. Automorphic forms extend these concepts to functions invariant under broader arithmetic groups, linking representation theory and algebraic geometry.
Historical Development of Automorphic and Modular Forms
The historical development of automorphic and modular forms traces back to the 19th century with the work of mathematicians such as Felix Klein and Henri Poincare. Modular forms originated from the theory of elliptic functions and complex analysis, while automorphic forms emerged as a generalization involving functions invariant under discrete groups acting on symmetric spaces. The evolution of these concepts significantly advanced number theory and representation theory, influencing the Langlands program and modern algebraic geometry.
Defining Automorphic Forms: Key Concepts
Automorphic forms generalize modular forms by extending transformation properties from the modular group to more general reductive algebraic groups over local and global fields. They are complex-valued functions on the upper half-plane or adelic groups, invariant under discrete group actions, satisfying specific growth and smoothness conditions. Central concepts include cuspidality, eigenfunction properties under Hecke operators, and connections to representation theory and number theory.
Defining Modular Forms: Key Properties
Modular forms are complex analytic functions defined on the upper half-plane that satisfy specific transformation properties under the action of the modular group, typically SL(2, Z). They exhibit modular invariance, meaning \( f\left(\frac{az+b}{cz+d}\right) = (cz+d)^k f(z) \) for integers \(a, b, c, d\) with \(ad - bc = 1\), where \(k\) is the weight of the form. Key properties include holomorphicity, Fourier expansion at cusps, and growth conditions ensuring their well-behaved nature at infinity, distinguishing them from more general automorphic forms.
Differences Between Automorphic and Modular Forms
Automorphic forms generalize modular forms by being defined on broader classes of groups and higher-dimensional symmetric spaces instead of just the modular group acting on the upper half-plane. While modular forms are complex analytic functions satisfying specific transformation properties under the action of SL(2,Z), automorphic forms extend this concept to reductive algebraic groups over global fields with more general invariance and growth conditions. The key difference lies in the scope: modular forms are a special case of automorphic forms with rich arithmetic and geometric structures tied specifically to SL(2,Z), whereas automorphic forms encompass a wider variety of groups and domains, allowing deeper applications in number theory and representation theory.
Similarities and Overlaps in Applications
Automorphic forms and modular forms both generalize complex analytic functions with transformation properties under discrete groups, playing significant roles in number theory and representation theory. They overlap in applications such as the study of L-functions, arithmetic geometry, and the Langlands program, where modular forms appear as specific cases of automorphic forms on the upper half-plane. These connections enable deep insights into prime distributions, elliptic curves, and the classification of algebraic objects through their shared symmetry and analytic properties.
Importance in Number Theory and Representation Theory
Automorphic forms generalize modular forms by extending their domain from the upper half-plane to more general symmetric spaces, playing a crucial role in number theory through the Langlands program which connects Galois representations and automorphic representations. Modular forms serve as fundamental building blocks in understanding arithmetic properties of elliptic curves, L-functions, and modularity theorems, while automorphic forms encapsulate these properties in a broader, representation-theoretic framework. Their importance lies in bridging harmonic analysis, algebraic geometry, and arithmetic via deep connections with the theory of automorphic representations and the spectral decomposition of L^2-spaces on arithmetic quotients.
Examples of Automorphic and Modular Forms
The modular form \( f(z) = \Delta(z) \), known as the Ramanujan delta function, exemplifies a cusp form of weight 12 for the modular group \( SL(2, \mathbb{Z}) \). Automorphic forms generalize modular forms by allowing invariance under a broader class of discrete groups acting on symmetric spaces, such as Maass wave forms associated with non-holomorphic automorphic representations of \( SL(2, \mathbb{R}) \). Classical examples of automorphic forms include Eisenstein series and holomorphic modular forms, both integral to the Langlands program and number theory research.
Modern Research and Breakthroughs
Recent breakthroughs in modern research have deepened the connection between automorphic forms and modular forms through the Langlands program, which predicts profound links between Galois representations and automorphic representations. Advances in the analytic theory of automorphic L-functions have led to significant progress in understanding the distribution of prime numbers and resolution of long-standing conjectures, such as the modularity theorem connecting elliptic curves to modular forms. Cutting-edge developments in p-adic automorphic forms and the expansion of the trace formula have opened new pathways in number theory and arithmetic geometry, revealing intricate symmetries underlying both automorphic and modular structures.
Conclusion: Implications for Mathematics
Automorphic forms generalize modular forms by extending the domain from the upper half-plane to more general symmetric spaces associated with Lie groups, enriching representation theory and number theory. These forms provide deeper insights into Langlands program connections, enabling advanced applications in arithmetic geometry and harmonic analysis. Understanding this relationship drives progress in solving longstanding problems in prime number distribution, elliptic curves, and beyond.
Automorphic form Infographic
 libterm.com
libterm.com