Haar measure provides a way to assign an invariant volume to subsets of locally compact topological groups, ensuring integration is well-defined and consistent under group translations. This concept plays a crucial role in harmonic analysis, representation theory, and ergodic theory by enabling the study of symmetries and group actions in a rigorous manner. Explore the rest of the article to understand how Haar measure impacts various mathematical fields and applications.
Table of Comparison
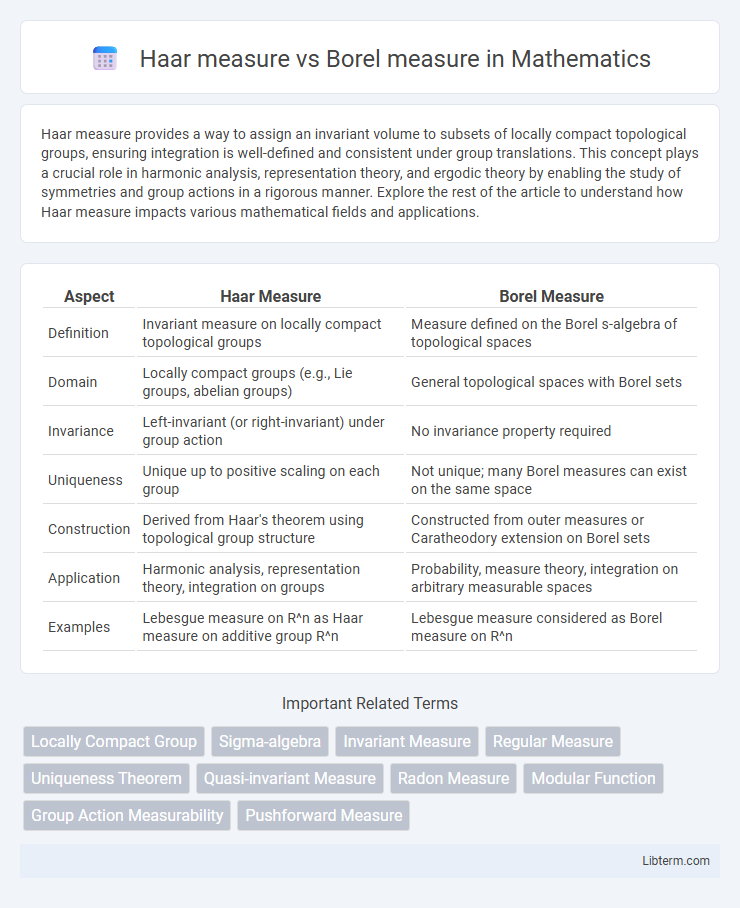
| Aspect | Haar Measure | Borel Measure |
|---|---|---|
| Definition | Invariant measure on locally compact topological groups | Measure defined on the Borel s-algebra of topological spaces |
| Domain | Locally compact groups (e.g., Lie groups, abelian groups) | General topological spaces with Borel sets |
| Invariance | Left-invariant (or right-invariant) under group action | No invariance property required |
| Uniqueness | Unique up to positive scaling on each group | Not unique; many Borel measures can exist on the same space |
| Construction | Derived from Haar's theorem using topological group structure | Constructed from outer measures or Caratheodory extension on Borel sets |
| Application | Harmonic analysis, representation theory, integration on groups | Probability, measure theory, integration on arbitrary measurable spaces |
| Examples | Lebesgue measure on R^n as Haar measure on additive group R^n | Lebesgue measure considered as Borel measure on R^n |
Introduction to Haar Measure and Borel Measure
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, essential for harmonic analysis and representation theory. Borel measure is defined on the s-algebra generated by open sets in a topological space, fundamental for probability theory and measure integration on general spaces. While Haar measure applies specifically to group structures ensuring left-invariance, Borel measure provides a broader framework applicable to any topological space.
Historical Background and Development
The concept of the Haar measure was introduced by Alfred Haar in 1933 as a means to define a translation-invariant measure on locally compact topological groups, which marked a significant advancement beyond the classical Borel measure originally developed for real line subsets. Borel measures, established earlier in the late 19th and early 20th centuries through the work of Emile Borel, provide a foundation for measure theory on metric spaces and standard Borel sets, mainly focusing on sigma-algebras generated by open sets. The development of Haar measure enabled rigorous analysis on more general algebraic structures such as Lie groups and paves the way for harmonic analysis and representation theory, extending the scope far beyond the initial Borel framework.
Fundamental Definitions
Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, essential for integrating functions over such groups consistently. Borel measure, constructed on the Borel s-algebra generated by open sets in a topological space, serves as a foundational framework for measure theory without inherent group structure or invariance properties. The fundamental distinction lies in Haar measure's invariance under group operations versus Borel measure's general applicability to measurable spaces without requiring group symmetry.
Key Properties of Haar Measure
Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, providing a consistent way to integrate functions over these groups. Unlike Borel measure, which is defined on the s-algebra generated by open sets and lacks translation invariance, Haar measure satisfies invariance under group operations, making it essential for harmonic analysis. Key properties include regularity, uniqueness up to a scalar multiple, and the ability to handle both compact and non-compact groups in a unified manner.
Key Properties of Borel Measure
Borel measures are defined on the s-algebra generated by open sets in a topological space, ensuring measurability of all Borel sets, which are countable unions and intersections of open and closed sets. Key properties include countable additivity, regularity (inner regularity by compact sets and outer regularity by open sets), and being finite on compact sets in locally compact spaces. Unlike Haar measure, which is translation-invariant on locally compact groups, Borel measures do not necessarily possess invariance properties but provide the foundational framework for measures on topological spaces.
Scope and Applications in Mathematics
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, crucial for harmonic analysis, representation theory, and ergodic theory. Borel measure, defined on the Borel s-algebra of any topological space, is more general and underpins measure theory, probability, and real analysis. While Haar measure applies specifically to group structures facilitating integration on groups, Borel measure's broader scope accommodates various spaces without group operations.
Comparisons: Haar vs Borel Measures
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, essential for harmonic analysis and representation theory, whereas Borel measure is a more general measure defined on the Borel sigma-algebra of topological spaces without requiring group structure. Haar measure ensures invariance under group operations, enabling integration on groups like Lie groups or compact groups, while Borel measures lack this invariance property and are primarily used in measure theory and probability on general topological spaces. The uniqueness and invariance of Haar measure make it critical in abstract harmonic analysis, contrasting with the broader applicability but less structured nature of Borel measures.
Invariance and Uniqueness Aspects
Haar measure is uniquely defined on locally compact topological groups with the key property of left-invariance, meaning it remains unchanged under group translation, which ensures consistent integration across the group structure. In contrast, Borel measure is defined on sigma-algebras generated by open sets in topological spaces and lacks inherent invariance properties, leading to non-uniqueness in measure assignments under transformations. The uniqueness of Haar measure up to a positive scalar multiple underlines its critical role in harmonic analysis and representation theory, whereas Borel measures are more general but do not offer this unique invariance framework.
Common Misconceptions and Challenges
The Haar measure is a unique translation-invariant measure defined on locally compact topological groups, whereas the Borel measure generally refers to measures defined on Borel s-algebras without requiring invariance properties. A common misconception is assuming all Borel measures on groups are Haar measures, ignoring the crucial requirement of invariance under group action critical to Haar measures. Challenges include understanding that the Haar measure exists only for locally compact groups and extending it consistently beyond Borel sets can be nontrivial, whereas Borel measures can lack such strong structural properties.
Summary and Further Reading
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, fundamentally used in harmonic analysis and representation theory, whereas Borel measure is defined on the Borel sigma-algebra of a topological space and is more general but not necessarily invariant under group actions. The Haar measure's invariance property makes it essential for integrating functions over groups and studying symmetry, while Borel measures provide the foundation for probability measures and integration in general topological settings. For further reading, consult "Abstract Harmonic Analysis" by E. Hewitt and K. Ross, and "Measure Theory" by Paul R. Halmos for foundational concepts on Borel measures.
Haar measure Infographic
 libterm.com
libterm.com