Newtonian physics forms the foundation of classical mechanics, describing the motion of objects based on Newton's laws of motion. Understanding these principles helps you analyze everyday phenomena from falling apples to planetary orbits. Explore the rest of the article to uncover how Newtonian concepts continue to influence modern science.
Table of Comparison
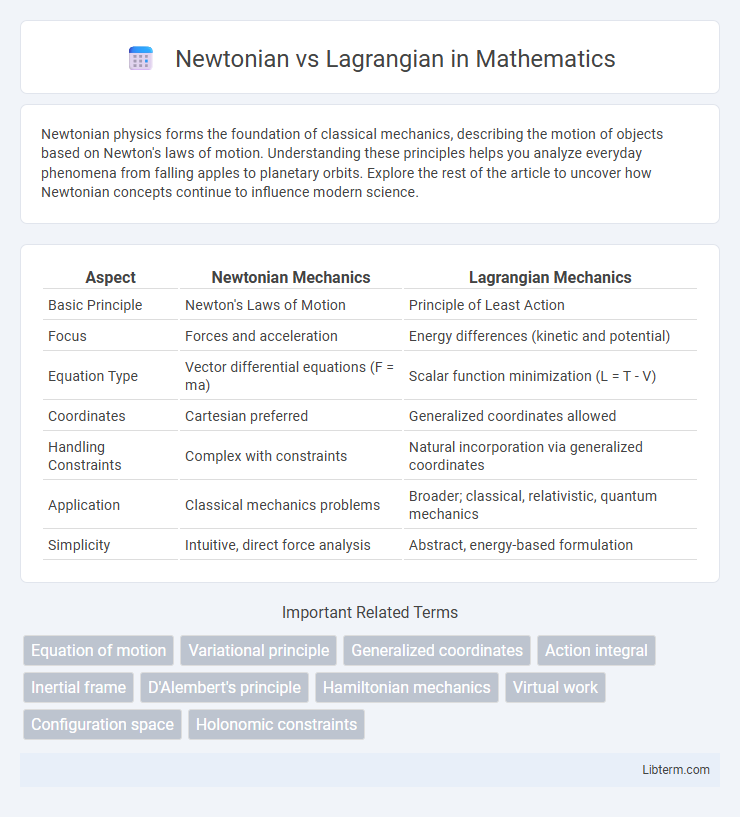
| Aspect | Newtonian Mechanics | Lagrangian Mechanics |
|---|---|---|
| Basic Principle | Newton's Laws of Motion | Principle of Least Action |
| Focus | Forces and acceleration | Energy differences (kinetic and potential) |
| Equation Type | Vector differential equations (F = ma) | Scalar function minimization (L = T - V) |
| Coordinates | Cartesian preferred | Generalized coordinates allowed |
| Handling Constraints | Complex with constraints | Natural incorporation via generalized coordinates |
| Application | Classical mechanics problems | Broader; classical, relativistic, quantum mechanics |
| Simplicity | Intuitive, direct force analysis | Abstract, energy-based formulation |
Introduction to Newtonian and Lagrangian Mechanics
Newtonian mechanics describes motion through forces acting on masses using vector quantities and differential equations based on Newton's laws of motion. Lagrangian mechanics reformulates classical mechanics by introducing the Lagrangian function, defined as the difference between kinetic and potential energy, leading to equations of motion derived from the principle of least action. This approach simplifies complex systems and constraints by focusing on energy transformations rather than forces, providing a powerful framework for analyzing mechanical systems.
Historical Background and Development
Newtonian mechanics, formulated in the 17th century by Sir Isaac Newton, laid the foundation for classical mechanics by describing motion through forces and acceleration using his three laws of motion. Lagrangian mechanics, developed in the 18th century by Joseph-Louis Lagrange, introduced a reformulation focusing on energy principles and generalized coordinates, providing a more versatile approach to complex systems. The transition from Newtonian to Lagrangian mechanics marked a significant evolution in theoretical physics, enabling advancements in analytical mechanics and influencing modern physics frameworks.
Fundamental Principles: Forces vs. Energies
Newtonian mechanics centers on forces and the direct application of Newton's laws of motion, emphasizing how forces cause acceleration in particles and rigid bodies. Lagrangian mechanics, built on the principle of least action, focuses on energies by formulating the system's dynamics through kinetic and potential energy functions. This energy-based approach simplifies complex systems, especially in constrained or non-Cartesian coordinates, offering a powerful alternative to force-based analysis.
Mathematical Formulation and Equations
Newtonian mechanics relies on vector equations of motion, primarily Newton's second law \( \mathbf{F} = m \mathbf{a} \), directly relating forces to accelerations in Cartesian coordinates. The Lagrangian formulation utilizes the scalar function \( L = T - V \), where \( T \) is kinetic energy and \( V \) is potential energy, leading to Euler-Lagrange equations \(\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q_i}} \right) - \frac{\partial L}{\partial q_i} = 0\) for generalized coordinates \( q_i \). This approach simplifies dynamics of systems with constraints and allows transformation to different coordinate systems seamlessly.
Degrees of Freedom in Both Approaches
Degrees of Freedom in Newtonian mechanics correspond directly to the number of independent coordinates required to describe a system's configuration, typically involving vector components of particle positions affected by external forces. In contrast, Lagrangian mechanics reduces the problem by introducing generalized coordinates, often less than the total Cartesian coordinates, which simplifies handling constraints and internal degrees of freedom. This approach streamlines dynamic equations by focusing on essential degrees of freedom related to energy functions rather than force vectors, making it particularly powerful for complex mechanical systems.
Applications in Classical Mechanics
Newtonian mechanics excels in solving problems involving forces and accelerations, making it ideal for analyzing particle motion and rigid body dynamics in engineering and physics. Lagrangian mechanics, leveraging generalized coordinates and energy principles, simplifies complex systems with constraints, such as in robotics and celestial mechanics. Both frameworks complement each other: Newtonian approaches offer intuitive force-based solutions, while Lagrangian methods enable efficient treatment of conservative systems and advanced mechanical modeling.
Advantages and Limitations
Newtonian mechanics offers straightforward equations of motion based on forces and accelerations, making it intuitive for analyzing simple systems with clearly defined forces. It faces limitations in handling complex constraints and non-inertial reference frames efficiently. Lagrangian mechanics advantages include the ability to elegantly incorporate constraints and generalized coordinates, providing a powerful framework for complex, multi-body, and constrained systems, though it can involve more abstract mathematical formulation and may require deep understanding of variational principles.
Transition from Newtonian to Lagrangian Framework
The transition from the Newtonian to the Lagrangian framework replaces vector forces and accelerations with scalar quantities like kinetic and potential energy, enabling the formulation of equations of motion through the principle of stationary action. This shift allows the use of generalized coordinates, making it easier to analyze systems with constraints and complex geometries. Lagrangian mechanics broadens the applicability beyond classical particle dynamics to fields such as quantum mechanics and relativity by focusing on energy functions rather than direct force analysis.
Real-World Examples and Case Studies
Newtonian mechanics excels in analyzing the trajectory of projectiles and calculating forces on rigid bodies, making it ideal for straightforward engineering problems like bridge design and vehicle dynamics. Lagrangian mechanics is preferred in complex systems with constraints, such as robotic arm movement and aerospace dynamics, where energy methods simplify equations of motion. Case studies in biomechanics demonstrate Newtonian approaches for joint force analysis, while Lagrangian methods effectively model multi-body dynamics in sports science and animal locomotion.
Conclusion: Choosing the Appropriate Method
Choosing between Newtonian and Lagrangian mechanics depends on the problem's complexity and constraints; Newtonian mechanics excels in straightforward systems with clear force interactions. Lagrangian mechanics offers powerful advantages in handling systems with constraints, generalized coordinates, and multi-body problems, simplifying equations of motion through energy principles. Selecting the appropriate method enhances problem-solving efficiency and clarity in classical mechanics analysis.
Newtonian Infographic
 libterm.com
libterm.com