A normal subgroup is a subgroup invariant under conjugation by any element of the parent group, playing a crucial role in the structure and classification of groups. It allows for the construction of quotient groups, which help simplify complex groups by identifying and collapsing certain elements. Explore the rest of this article to understand how normal subgroups function and their importance in group theory.
Table of Comparison
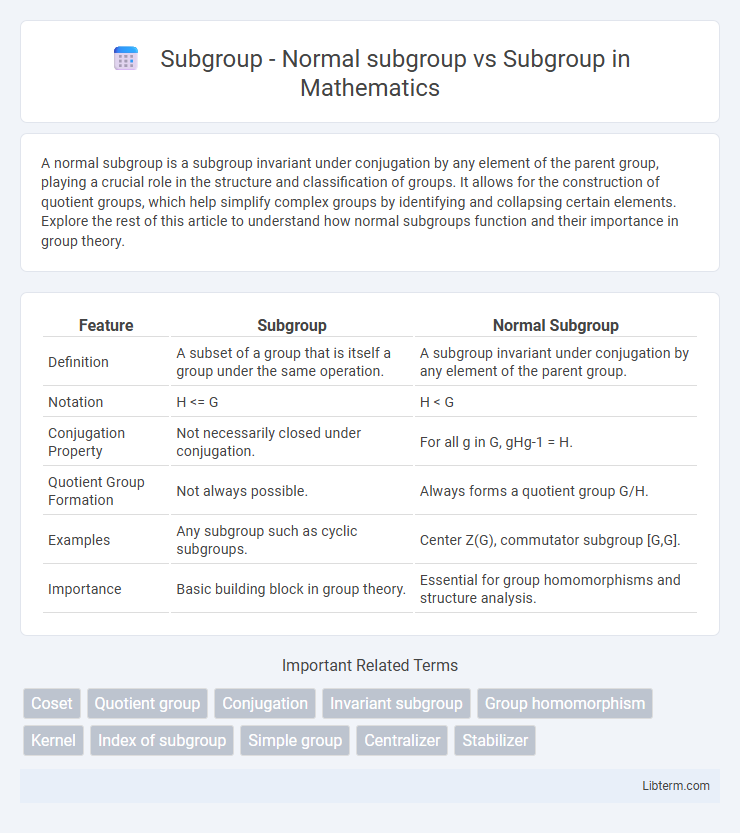
| Feature | Subgroup | Normal Subgroup |
|---|---|---|
| Definition | A subset of a group that is itself a group under the same operation. | A subgroup invariant under conjugation by any element of the parent group. |
| Notation | H <= G | H < G |
| Conjugation Property | Not necessarily closed under conjugation. | For all g in G, gHg-1 = H. |
| Quotient Group Formation | Not always possible. | Always forms a quotient group G/H. |
| Examples | Any subgroup such as cyclic subgroups. | Center Z(G), commutator subgroup [G,G]. |
| Importance | Basic building block in group theory. | Essential for group homomorphisms and structure analysis. |
Understanding Subgroups: A Fundamental Concept
A subgroup is a subset of a group that itself forms a group under the same operation, satisfying closure, associativity, identity, and invertibility. A normal subgroup is a special type of subgroup invariant under conjugation by any element of the original group, allowing the formation of quotient groups. Understanding the distinction between subgroups and normal subgroups is essential for exploring group structure and algebraic homomorphisms.
Defining Subgroups in Group Theory
A subgroup in group theory is a subset of a group that itself forms a group under the same operation. A normal subgroup is a special type of subgroup where every left coset is also a right coset, allowing the formation of quotient groups. This property makes normal subgroups fundamental in studying group homomorphisms and group structure decomposition.
What Makes a Subgroup? Key Properties
A subgroup H of a group G must satisfy three key properties: closure under the group operation, existence of the identity element of G within H, and inclusion of inverses for every element in H. Normal subgroups, a special type of subgroup, further require that for every element g in G and h in H, the element g h g-1 also lies in H, ensuring invariant structure under conjugation. This normality condition is essential for constructing quotient groups and facilitates group homomorphisms and factorization in group theory.
Introduction to Normal Subgroups
A normal subgroup is a specific type of subgroup within a group that remains invariant under conjugation by any element of the parent group, satisfying the condition \( gNg^{-1} = N \) for all \( g \in G \). Unlike general subgroups, normal subgroups enable the construction of quotient groups, forming the foundation for many group theory applications. This property facilitates the study of group structure through homomorphisms and group actions.
Distinguishing Subgroups and Normal Subgroups
Subgroups are subsets of a group that themselves form a group under the same operation, while normal subgroups are subgroups invariant under conjugation by elements of the entire group. The key distinction lies in the property gNg-1 = N for all g in the group, making normal subgroups suitable for quotient group construction. Identifying normal subgroups is crucial in analyzing group homomorphisms and understanding group structure.
Criteria for Normality in Subgroups
A subgroup H of a group G is normal if it is invariant under conjugation by any element of G, meaning for every g in G, the element gHg-1 is contained in H. This criterion ensures that the left and right cosets of H in G coincide, which is a fundamental property distinguishing normal subgroups from arbitrary subgroups. Normality allows the construction of quotient groups, playing a crucial role in the classification and analysis of group structure.
Examples of Subgroups vs Normal Subgroups
Subgroups, such as the set of even integers within the integers under addition, are subsets that satisfy group properties but may not remain invariant under conjugation by all group elements. Normal subgroups, for example, the center of a group or the kernel of a group homomorphism, are special subgroups that remain fixed under conjugation, enabling the construction of quotient groups. An example illustrating the difference is the subgroup of rotations in a dihedral group, which is normal, whereas the subgroup of reflections is not, demonstrating how normality depends on conjugation invariance.
Importance of Normal Subgroups in Group Structure
Normal subgroups are essential in group theory because they allow the construction of quotient groups, enabling a deeper analysis of a group's internal structure. Unlike general subgroups, normal subgroups remain invariant under conjugation by any group element, making them pivotal for defining homomorphisms and facilitating group decomposition. Understanding normal subgroups aids in classifying groups and studying their properties through factor groups and group homomorphisms.
Applications: Where Normal Subgroups Matter
Normal subgroups play a critical role in group theory applications such as constructing quotient groups, which are fundamental in understanding group homomorphisms and classification of groups. Unlike general subgroups, normal subgroups enable the definition of group actions on cosets, facilitating symmetry analysis in algebraic structures and solving problems in Galois theory. These properties are essential in cryptography, coding theory, and the study of algebraic topology, where normality ensures consistent and well-defined group factorization.
Summary: Comparing Normal Subgroups and Subgroups
Normal subgroups are a specific type of subgroup where every left coset is also a right coset, ensuring that the subgroup is invariant under conjugation by any group element. In contrast, a general subgroup does not require this invariance and may not satisfy the normality condition. This distinction is crucial for constructing quotient groups, as only normal subgroups guarantee a well-defined group structure on the set of cosets.
Subgroup - Normal subgroup Infographic
 libterm.com
libterm.com