A nilpotent group is a type of group in abstract algebra where the upper central series terminates at the group itself after finitely many steps. These groups generalize the concept of abelian groups by allowing a more flexible but still highly structured hierarchy. Explore the article to understand how nilpotent groups reveal deep insights into group theory and their applications.
Table of Comparison
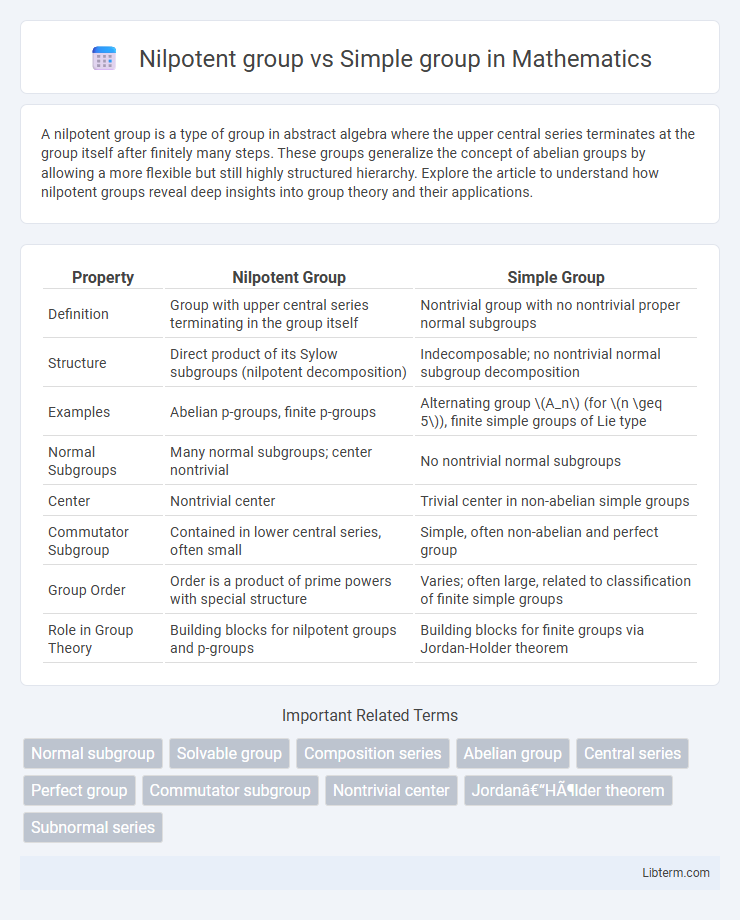
| Property | Nilpotent Group | Simple Group |
|---|---|---|
| Definition | Group with upper central series terminating in the group itself | Nontrivial group with no nontrivial proper normal subgroups |
| Structure | Direct product of its Sylow subgroups (nilpotent decomposition) | Indecomposable; no nontrivial normal subgroup decomposition |
| Examples | Abelian p-groups, finite p-groups | Alternating group \(A_n\) (for \(n \geq 5\)), finite simple groups of Lie type |
| Normal Subgroups | Many normal subgroups; center nontrivial | No nontrivial normal subgroups |
| Center | Nontrivial center | Trivial center in non-abelian simple groups |
| Commutator Subgroup | Contained in lower central series, often small | Simple, often non-abelian and perfect group |
| Group Order | Order is a product of prime powers with special structure | Varies; often large, related to classification of finite simple groups |
| Role in Group Theory | Building blocks for nilpotent groups and p-groups | Building blocks for finite groups via Jordan-Holder theorem |
Introduction to Nilpotent and Simple Groups
Nilpotent groups are characterized by their upper central series terminating at the group itself, reflecting a highly structured, stepwise commutativity that generalizes abelian groups. Simple groups, in contrast, have no nontrivial normal subgroups, making them the fundamental building blocks in group theory through the classification of finite simple groups. Understanding nilpotent groups involves examining their decomposable structure and centralizers, while the study of simple groups focuses on their indivisibility and role in symmetry and algebraic systems.
Defining Nilpotent Groups
Nilpotent groups are defined by their upper central series terminating in the entire group after finitely many steps, emphasizing a highly structured form of commutativity. Simple groups, in contrast, contain no nontrivial normal subgroups, making them building blocks for all finite groups unlike nilpotent groups, which have a rich normal subgroup structure. The concept of nilpotency hinges on the group's center and commutator subgroups, reflecting intricate internal symmetry properties.
Defining Simple Groups
Simple groups are nontrivial groups whose only normal subgroups are the trivial subgroup and the group itself, serving as building blocks in group theory. In contrast, nilpotent groups possess a central series terminating in the trivial subgroup, exhibiting a highly decomposable and hierarchical structure. Defining simple groups highlights their role in classifying all finite groups through composition series without nontrivial normal subgroups.
Key Structural Differences
Nilpotent groups possess a central series with all factors in the center, ensuring every Sylow subgroup is normal, resulting in a highly decomposable and hierarchical internal structure. Simple groups, in contrast, lack nontrivial normal subgroups, making them indivisible building blocks in group theory with no nontrivial normal factorization. The key structural difference lies in normal subgroup behavior: nilpotent groups have rich normal subgroup lattices, while simple groups have only trivial and total normal subgroups, reflecting fundamentally distinct organizational frameworks.
Examples of Nilpotent Groups
Nilpotent groups often include examples such as p-groups, where every element's order is a power of a prime p, highlighting their strong hierarchical structure with a central series terminating in the trivial subgroup. In contrast, simple groups like A5, the alternating group on five elements, possess no nontrivial normal subgroups, reflecting their indivisibility and complexity. The Heisenberg group over integers illustrates a classic nilpotent group example characterized by its upper-triangular matrix form and stepwise commutator reductions.
Examples of Simple Groups
Examples of simple groups include the alternating groups An for n >= 5 and the projective special linear groups PSL(2, p) where p is a prime number. Simple groups have no nontrivial normal subgroups, making them the building blocks in the classification of finite groups, unlike nilpotent groups, which have a central series terminating in the trivial group. The smallest non-abelian simple group is A5, of order 60, serving as a fundamental example in group theory.
Group Properties: Center and Normal Subgroups
Nilpotent groups have a nontrivial center, meaning their center contains elements beyond the identity, which guarantees a rich structure of normal subgroups forming an ascending central series. Simple groups possess a trivial center, consisting only of the identity element, and lack nontrivial normal subgroups, highlighting their indivisible nature in group theory. The presence of a nontrivial center in nilpotent groups contrasts sharply with the minimal normal subgroup structure of simple groups, emphasizing key differences in their internal symmetry and subgroup composition.
Classification and Importance in Group Theory
Nilpotent groups are classified by their upper central series terminating at the whole group, highlighting their intricate internal structure through normal subgroups, while simple groups feature no nontrivial normal subgroups and serve as fundamental building blocks in the classification of all finite groups. The classification of finite simple groups, a monumental achievement in group theory, provides a comprehensive list of all simple groups, including cyclic groups of prime order, alternating groups, and groups of Lie type. Understanding nilpotent groups is crucial for studying group extensions and solvability, whereas simple groups underpin the structural decomposition of complex groups, making both pivotal in the development and application of modern algebraic theory.
Applications in Mathematics and Beyond
Nilpotent groups play a crucial role in algebraic topology and group theory due to their well-understood structure, facilitating the classification of solvable systems and the analysis of p-groups in number theory. Simple groups, especially finite simple groups, underpin the classification of all finite groups and are instrumental in understanding symmetry in geometry, cryptography, and theoretical physics. Applications extend beyond pure mathematics to coding theory, quantum computation, and particle physics where group symmetry principles are foundational.
Summary: Nilpotent vs Simple Groups
Nilpotent groups are characterized by a central series with all factors in the center, ensuring all Sylow subgroups are normal and the group is solvable; simple groups have no nontrivial normal subgroups and serve as building blocks in group theory. Nilpotent groups exhibit strong structural constraints and decomposability, while simple groups, especially non-abelian ones, are highly non-decomposable and often complex. Understanding these distinctions is critical for classifying finite groups and analyzing their subgroup structures.
Nilpotent group Infographic
 libterm.com
libterm.com