The pin structure is a crucial element in electronics, defining the arrangement and function of individual pins on a component or connector. Each pin serves a specific purpose, such as power supply, grounding, or signal transmission, contributing to the overall performance of the device. Explore the rest of this article to understand how the pin structure impacts your electronic projects and device compatibility.
Table of Comparison
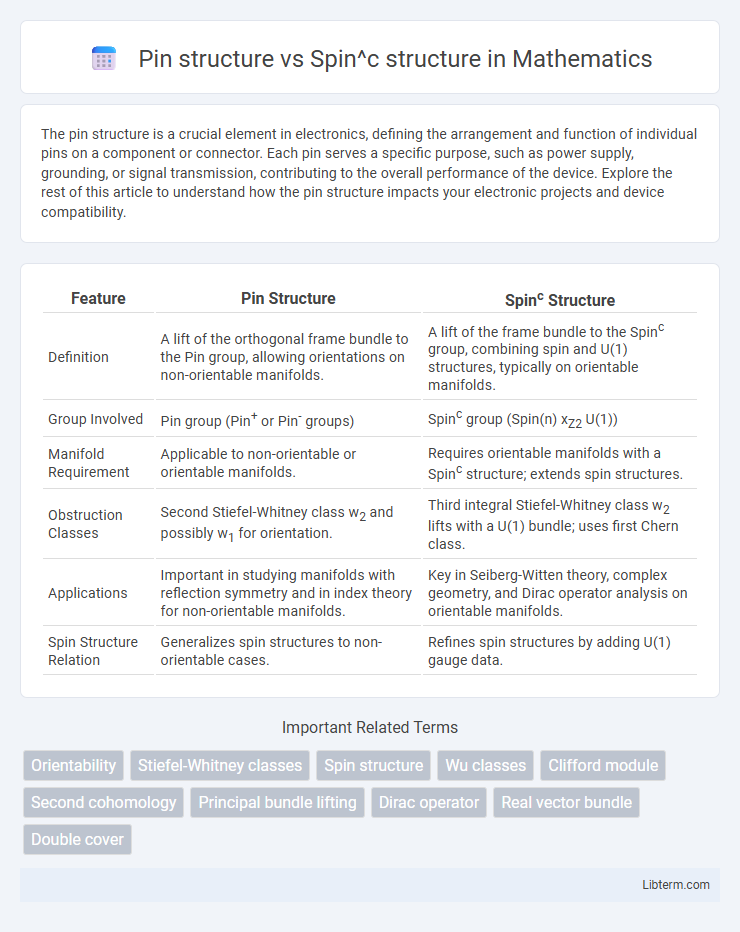
| Feature | Pin Structure | Spinc Structure |
|---|---|---|
| Definition | A lift of the orthogonal frame bundle to the Pin group, allowing orientations on non-orientable manifolds. | A lift of the frame bundle to the Spinc group, combining spin and U(1) structures, typically on orientable manifolds. |
| Group Involved | Pin group (Pin+ or Pin- groups) | Spinc group (Spin(n) xZ2 U(1)) |
| Manifold Requirement | Applicable to non-orientable or orientable manifolds. | Requires orientable manifolds with a Spinc structure; extends spin structures. |
| Obstruction Classes | Second Stiefel-Whitney class w2 and possibly w1 for orientation. | Third integral Stiefel-Whitney class w2 lifts with a U(1) bundle; uses first Chern class. |
| Applications | Important in studying manifolds with reflection symmetry and in index theory for non-orientable manifolds. | Key in Seiberg-Witten theory, complex geometry, and Dirac operator analysis on orientable manifolds. |
| Spin Structure Relation | Generalizes spin structures to non-orientable cases. | Refines spin structures by adding U(1) gauge data. |
Introduction to Pin and Spin^c Structures
Pin structures generalize spin structures to non-orientable manifolds by lifting the orthogonal group O(n) to its double cover Pin(n), allowing the definition of spinors in contexts where orientation is not fixed. Spin^c structures extend spin structures by incorporating a U(1) principal bundle, providing a framework for defining spinors on oriented manifolds with additional complex line bundles and enabling applications in gauge theory and complex geometry. Both Pin and Spin^c structures play crucial roles in topology and mathematical physics by facilitating the analysis of manifolds with constrained structural properties.
Mathematical Foundations of Pin Structures
Pin structures generalize spin structures to non-orientable manifolds by lifting the frame bundle to the Pin group, a double cover of the orthogonal group O(n), unlike the Spin group which covers SO(n). The mathematical foundation of Pin structures involves constructing a principal Pin bundle that captures the topological obstruction represented by the first and second Stiefel-Whitney classes, w_1 and w_2. These structures enable defining Dirac operators and analyzing fermions on non-orientable manifolds, extending the applications of spin geometry in differential topology and mathematical physics.
Overview of Spin^c Structures
Spin^c structures generalize spin structures by incorporating a U(1) gauge symmetry, allowing for the definition of spinors on manifolds that may not admit a spin structure. They are crucial in differential geometry and theoretical physics, particularly in the study of Dirac operators and Seiberg-Witten theory. Unlike Pin structures, which relate to reflections and time-reversal symmetries in non-orientable manifolds, Spin^c structures exist on oriented manifolds and provide a framework for coupling spinors with electromagnetic fields.
Key Differences Between Pin and Spin^c Structures
Pin structures generalize Spin structures to manifolds that may be non-orientable, enabling the definition of spinors on such spaces, while Spin^c structures extend Spin structures by incorporating an additional U(1) gauge symmetry, useful for defining spinors coupled to electromagnetic fields. Pin structures are associated with lifting the orthogonal group O(n) to its double cover Pin(n), which splits into Pin+ and Pin- types depending on the choice of Clifford algebra, whereas Spin^c structures lift the special orthogonal group SO(n) to a group that is a central extension by U(1), combining Spin and complex line bundles. The key difference lies in their applicability--Pin structures manage non-orientable manifolds and real spinors, whereas Spin^c structures are defined on orientable manifolds and facilitate the coupling of spinors with complex line bundles and gauge fields.
Topological Obstructions and Existence Conditions
Topological obstructions to the existence of a Pin structure on a manifold are governed by the second Stiefel-Whitney class \( w_2 \) and the first Stiefel-Whitney class \( w_1 \), with a Pin structure existing if and only if these classes satisfy specific lifting conditions related to the Pin group extensions. In contrast, a Spin^c structure requires the vanishing of the third integral Stiefel-Whitney class and the existence of an auxiliary complex line bundle, linking the obstruction to a lift of the principal \( SO(n) \)-bundle to the Spin^c group. The precise existence conditions involve integral cohomology classes, where Spin structures demand \( w_2 = 0 \), Pin structures allow \( w_2 + w_1^2 = 0 \) mod 2, and Spin^c structures require \( w_2 \) to be the mod 2 reduction of an integral class, reflecting the different topological and geometric constraints.
Applications in Differential Geometry and Topology
Pin structures generalize Spin^c structures by allowing a manifold to admit orientation-reversing symmetries, crucial in studying non-orientable manifolds and their Dirac operators in differential geometry. Spin^c structures extend Spin structures by incorporating a complex line bundle, enabling the definition of Dirac operators on oriented manifolds with U(1) gauge fields, which are essential in index theory and Seiberg-Witten invariants in four-dimensional topology. Both structures facilitate the analysis of fermionic fields and topological quantum field theories, linking geometry with gauge theory and cobordism classifications.
Role in Physics: Fermions and Gauge Fields
Pin structures and Spin^c structures are crucial in describing fermions on manifolds with different types of symmetry constraints in physics; Pin structures generalize Spin structures to include reflections and time-reversal symmetries, enabling the definition of fermions on non-orientable manifolds. Spin^c structures incorporate an additional U(1) gauge field, allowing the coupling of fermions to electromagnetic fields and playing a central role in gauge theories and complex line bundles. The choice between Pin and Spin^c structures dictates the types of fermionic fields and gauge interactions that can be consistently defined, influencing topological phases and anomalies in quantum field theories.
Examples on Manifolds: Pin vs Spin^c Cases
Pin structures on manifolds arise when considering real vector bundles with reflections, typically defined on non-orientable manifolds like the Mobius strip or the Klein bottle, enabling the lifting of the orthogonal group O(n) to Pin(n). Spin^c structures, by contrast, are defined on oriented manifolds such as complex projective spaces or Kahler manifolds, combining Spin(n) structures with a U(1)-bundle to incorporate complex line bundles and enabling a lift from SO(n) x U(1) to Spin^c(n). For example, the real projective plane RP^2, which is non-orientable, admits Pin structures but no Spin or Spin^c structures, while the two-dimensional torus T^2, an orientable manifold, admits Spin and Spin^c structures but no Pin structures.
Orientation and Bundle Lifting Problems
Pin structures generalize Spin structures to non-orientable manifolds by providing a framework for lifting the frame bundle to a Pin group, addressing orientation-reversal symmetries that Spin^c structures, defined on oriented manifolds, do not account for. Spin^c structures refine Spin structures by incorporating a complex line bundle, enabling bundle lifting through a U(1) extension that resolves certain topological obstructions, specifically those related to the second Stiefel-Whitney class and orientation. The key orientation difference lies in Pin structures working over unoriented manifolds by lifting to Pin groups (Pin^+ or Pin^-), whereas Spin^c structures require orientability and facilitate lifting through Spin x U(1), blending spin geometry with complex line bundles.
Summary Table: Pin Structure vs Spin^c Structure
Pin structures generalize spin structures to manifolds that may be non-orientable, allowing for the definition of spinors on such manifolds, while Spin^c structures extend spin structures by incorporating a U(1) bundle, enabling the study of manifolds with complex line bundles or magnetic monopoles. The summary table highlights key differences: Pin structures relate to real vector bundles with an emphasis on reflection symmetry and obstruction given by the first and second Stiefel-Whitney classes, whereas Spin^c structures involve complex vector bundles, use first Chern classes, and require both orientation and a choice of complex structure. Pin structures arise from the Pin group (Pin+, Pin-), accommodating non-orientability, and Spin^c structures stem from the Spin^c group, combining Spin groups with circle groups to adapt to complex geometry and gauge fields.
Pin structure Infographic
 libterm.com
libterm.com