A direct limit is a fundamental concept in category theory and abstract algebra that allows the construction of a universal object from a directed system of objects and morphisms. This process unifies and extends structures by capturing the collective behavior of an increasing sequence or net of elements. Explore the rest of the article to understand how a direct limit operates and applies to your mathematical studies.
Table of Comparison
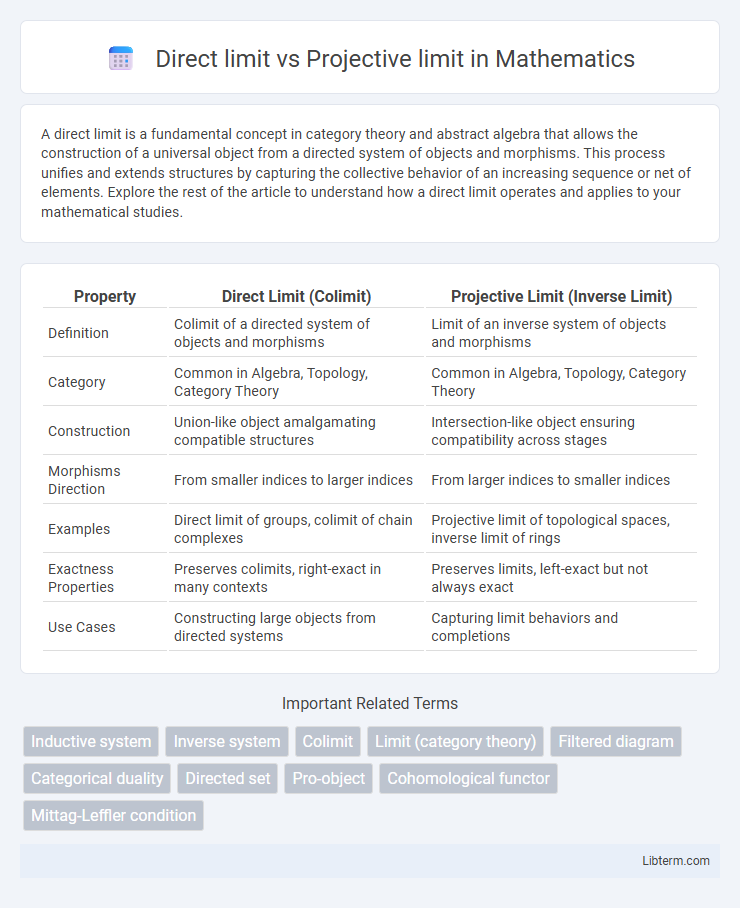
| Property | Direct Limit (Colimit) | Projective Limit (Inverse Limit) |
|---|---|---|
| Definition | Colimit of a directed system of objects and morphisms | Limit of an inverse system of objects and morphisms |
| Category | Common in Algebra, Topology, Category Theory | Common in Algebra, Topology, Category Theory |
| Construction | Union-like object amalgamating compatible structures | Intersection-like object ensuring compatibility across stages |
| Morphisms Direction | From smaller indices to larger indices | From larger indices to smaller indices |
| Examples | Direct limit of groups, colimit of chain complexes | Projective limit of topological spaces, inverse limit of rings |
| Exactness Properties | Preserves colimits, right-exact in many contexts | Preserves limits, left-exact but not always exact |
| Use Cases | Constructing large objects from directed systems | Capturing limit behaviors and completions |
Introduction to Direct and Projective Limits
Direct limits, also known as colimits, capture the idea of unifying an ascending sequence of algebraic structures or topological spaces through compatible morphisms, enabling the construction of larger objects that coherently encapsulate all prior ones. Projective limits, or inverse limits, provide a way to systematically "glue" together a family of objects indexed by a directed set via consistent projections, producing an object that reflects all the approximations simultaneously. Both limits play crucial roles in category theory and algebraic topology by formalizing the passage from local to global properties through the use of diagrams indexed over directed sets.
Fundamental Concepts in Category Theory
Direct limits in category theory capture the colimit of a directed system of objects and morphisms, representing a universal object factoring all maps coherently. Projective limits, or inverse limits, form the limit of an inverse system, yielding an object together with morphisms that satisfy compatibility conditions with respect to projection maps. These fundamental constructions provide dual ways to understand how complex objects arise from simpler components through universal properties in various categories.
Defining Direct (Inductive) Limits
Direct limits, also known as inductive limits, are defined as the colimit of a directed system of objects and morphisms in a category, capturing the idea of "passing to the limit" along an increasing chain. They provide a universal object receiving compatible morphisms from each object in the system, effectively amalgamating the structure into a single entity. This construction is fundamental in algebra, topology, and category theory for analyzing systems that grow or refine over time.
Defining Projective (Inverse) Limits
Projective (inverse) limits define a way to construct an object by taking the limit of a directed system of spaces or groups linked through morphisms going "backwards" along a directed set. Formally, the projective limit of a family {(X_i, f_{ij})} consists of the subset of the Cartesian product X_i where elements are compatible under the bonding maps f_{ij}: X_j - X_i for i <= j. This construction is key in topology, algebra, and category theory for encoding limits of inverse systems, enabling the reconstruction of complex structures from simpler approximations.
Key Differences Between Direct and Projective Limits
Direct limits capture the colimit of a directed system, combining objects through inductive processes to form a universal object representing all inclusions. Projective limits, or inverse limits, construct a universal object via a projective system, encoding compatibility across projections in a limit. Key differences include that direct limits preserve colimits and typically appear in constructions involving unions or increasing sequences, while projective limits preserve limits and often model intersections or inverse systems with projection maps.
Examples of Direct Limits in Mathematics
Direct limits in mathematics commonly appear in algebraic topology, where the direct limit of a sequence of homology groups captures the stable homology of an increasing union of spaces. For instance, the direct limit of a directed system of abelian groups \( \{G_i, f_{ij}\} \) is used to define the homology groups of infinite complexes by taking the colimit of finite subcomplexes. Another example arises in module theory, where the direct limit constructs modules over rings by linking chains of submodules, enabling the study of properties preserved under direct unions.
Examples of Projective Limits in Mathematics
Projective limits in mathematics often appear in the construction of p-adic integers, where the system consists of inverse limits of the rings \(\mathbb{Z}/p^n\mathbb{Z}\) under natural projection maps. Another notable example is the inverse limit of topological spaces used to define the Cantor set as a projective limit of finite discrete spaces. These examples illustrate how projective limits capture infinite structures through consistent finite approximations, preserving algebraic and topological properties in the limit.
Applications in Algebra and Topology
Direct limits enable the construction of larger algebraic structures from directed systems, crucial for defining colimits in categories like modules, groups, and vector spaces, facilitating the study of inductive constructions in algebra. Projective limits assemble inverse systems into limiting objects, essential for understanding completions, profinite groups, and inverse limits of topological spaces, underpinning the analysis of continuity and compactness properties. In topology, direct limits model increasing unions of spaces, while projective limits capture spaces defined by compatible families of projections, supporting dual perspectives in homological algebra and shape theory.
Importance in Modern Mathematical Research
Direct limits and projective limits play a crucial role in modern mathematical research by enabling the construction of objects from directed systems and inverse systems, respectively, allowing mathematicians to understand complex structures through simpler components. Direct limits facilitate the study of algebraic and topological objects by capturing colimits in categories such as modules, groups, and sheaves, which is fundamental for homological algebra and category theory. Projective limits, or inverse limits, are essential in areas like number theory, algebraic geometry, and functional analysis, providing a framework to analyze continuity, completions, and profinite groups through the inverse system of approximations.
Summary and Comparative Insights
Direct limits represent colimits in category theory, capturing the universal object receiving morphisms from an ascending sequence of objects, often used in algebra and topology to describe inductive systems. Projective limits, or inverse limits, form limits from a descending sequence of objects with morphisms directed oppositely, crucial for constructing objects like completions, profinite groups, and sheaves. The key difference lies in the direction of morphisms and their universal properties: direct limits aggregate data up to a "union," while projective limits enforce consistency across "projections," highlighting their dual nature in mathematical structures.
Direct limit Infographic
 libterm.com
libterm.com