Negative definite matrices have all their eigenvalues strictly less than zero, ensuring that quadratic forms always produce negative values except at the origin. This property is central in stability analysis and optimization problems where identifying maxima is critical. Explore the rest of the article to deepen your understanding of negative definiteness and its practical applications.
Table of Comparison
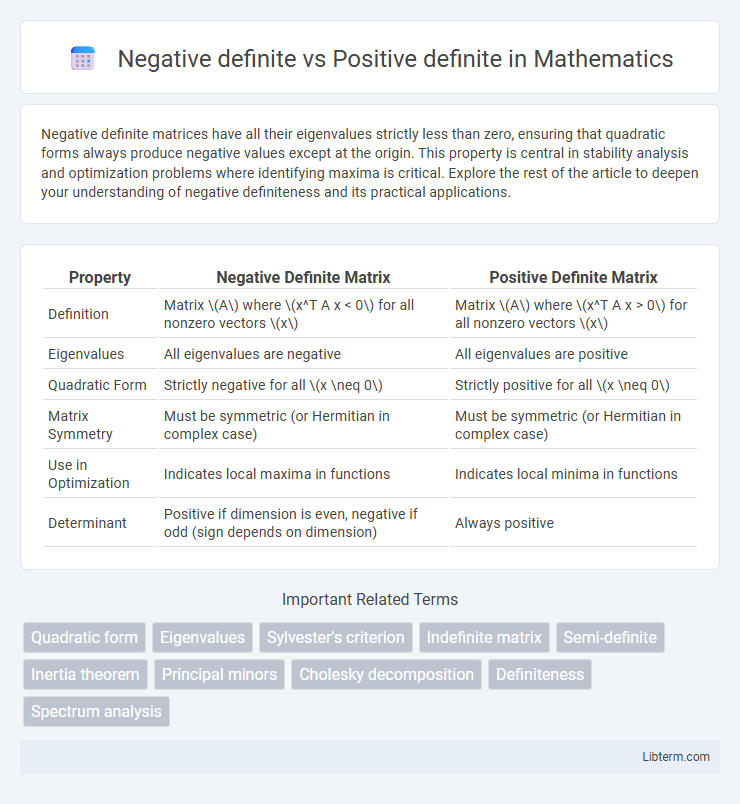
| Property | Negative Definite Matrix | Positive Definite Matrix |
|---|---|---|
| Definition | Matrix \(A\) where \(x^T A x < 0\) for all nonzero vectors \(x\) | Matrix \(A\) where \(x^T A x > 0\) for all nonzero vectors \(x\) |
| Eigenvalues | All eigenvalues are negative | All eigenvalues are positive |
| Quadratic Form | Strictly negative for all \(x \neq 0\) | Strictly positive for all \(x \neq 0\) |
| Matrix Symmetry | Must be symmetric (or Hermitian in complex case) | Must be symmetric (or Hermitian in complex case) |
| Use in Optimization | Indicates local maxima in functions | Indicates local minima in functions |
| Determinant | Positive if dimension is even, negative if odd (sign depends on dimension) | Always positive |
Introduction to Definite Matrices
Definite matrices are classified based on the sign of their quadratic forms, where a positive definite matrix produces strictly positive values for all non-zero vectors, ensuring important properties like invertibility and stability in optimization. Negative definite matrices yield strictly negative quadratic forms for all non-zero vectors, often indicating concavity in functions and stability in certain dynamical systems. Understanding these distinctions is crucial in fields such as linear algebra, optimization, and control theory for characterizing matrix behavior and solution properties.
Defining Positive Definite Matrices
Positive definite matrices are square, symmetric matrices characterized by all their eigenvalues being strictly positive, ensuring that for any non-zero vector x, the quadratic form xTAx is greater than zero. This property guarantees that positive definite matrices are invertible and correspond to positive curvature in optimization problems and covariance matrices in statistics. Understanding the distinction from negative definite matrices, which have strictly negative eigenvalues and yield xTAx less than zero, is crucial for applications in numerical analysis and machine learning.
Understanding Negative Definite Matrices
Negative definite matrices have all their eigenvalues strictly less than zero, ensuring that for any nonzero vector \(x\), the quadratic form \(x^T A x\) is negative. This property plays a crucial role in optimization problems, stability analysis, and understanding concavity in multivariate functions. Recognizing negative definiteness involves checking symmetry and eigenvalue conditions, distinguishing these matrices from positive definite matrices, which have strictly positive eigenvalues and produce positive quadratic forms.
Key Properties: Positive vs Negative Definite
Positive definite matrices are symmetric with all positive eigenvalues, ensuring strict convexity in quadratic forms and guaranteeing unique global minima in optimization. Negative definite matrices are also symmetric but possess all negative eigenvalues, indicating strict concavity and unique global maxima in their associated quadratic forms. Key properties include positive definiteness implying positive values for xTAx for all nonzero vectors x, while negative definiteness means xTAx is always negative for all nonzero x.
Eigenvalues and Definiteness
Negative definite matrices have all eigenvalues strictly less than zero, ensuring that for any nonzero vector x, the quadratic form xTAx is negative, confirming the matrix's negative definiteness. Positive definite matrices possess all strictly positive eigenvalues, guaranteeing that xTAx is positive for any nonzero vector x, a key property in optimization and stability analysis. Eigenvalue distribution directly determines definiteness: strictly positive eigenvalues imply positive definiteness, strictly negative imply negative definiteness, while mixed or zero eigenvalues indicate indefinite or semidefinite matrices.
Testing for Positive or Negative Definiteness
Testing for positive or negative definiteness of a matrix involves checking the signs of its eigenvalues or principal minors. A matrix is positive definite if all its eigenvalues are positive and all leading principal minors are greater than zero. Conversely, negative definiteness requires all eigenvalues to be negative and the principal minors to alternate in sign starting with negative.
Applications in Machine Learning and Optimization
Negative definite matrices are crucial in machine learning for defining concave functions, which help ensure convergence to global maxima in optimization problems like maximization of likelihood functions. Positive definite matrices guarantee convexity in optimization, enabling efficient solutions in algorithms such as support vector machines and Gaussian processes by ensuring unique global minima. Both matrix types are fundamental in Hessian matrix analysis, stability assessments, and regularization techniques in high-dimensional data modeling.
Common Examples and Counterexamples
Positive definite matrices, such as the identity matrix and covariance matrices in statistics, have all positive eigenvalues, ensuring properties like convexity and stability in optimization problems. Negative definite matrices, exemplified by the negative identity matrix or the Hessian of concave functions at maximum points, have all negative eigenvalues, indicating local maxima in optimization contexts. A common counterexample is the indefinite matrix, which has both positive and negative eigenvalues, such as the matrix [[0,1],[1,0]], showing neither positive nor negative definiteness.
Implications in Quadratic Forms
Negative definite quadratic forms always yield strictly negative values for any nonzero vector input, indicating concave curvature in optimization problems. Positive definite quadratic forms generate strictly positive values for all nonzero vectors, representing convex curvature and guaranteeing unique global minima in quadratic optimization. These properties directly influence stability analysis, eigenvalue distribution, and the nature of critical points in multivariate functions.
Summary: Choosing the Right Matrix Type
Negative definite matrices have all eigenvalues less than zero, which ensures energy functions decrease and systems are stable in certain dynamic models. Positive definite matrices, with all eigenvalues greater than zero, guarantee convexity and are essential in optimization for confirming local minima. Selecting the right matrix type depends on the application requirements: use positive definite matrices for stability in optimization problems and negative definite matrices for representing stable equilibria in dynamical systems.
Negative definite Infographic
 libterm.com
libterm.com