An integrally closed domain is a type of integral domain where every element integral over the domain actually lies within it, ensuring no missing algebraic elements in its field of fractions. This property is crucial in algebraic geometry and number theory, as it guarantees the domain is free from certain types of algebraic singularities. Explore the rest of the article to understand how integrally closed domains influence key mathematical structures and your research.
Table of Comparison
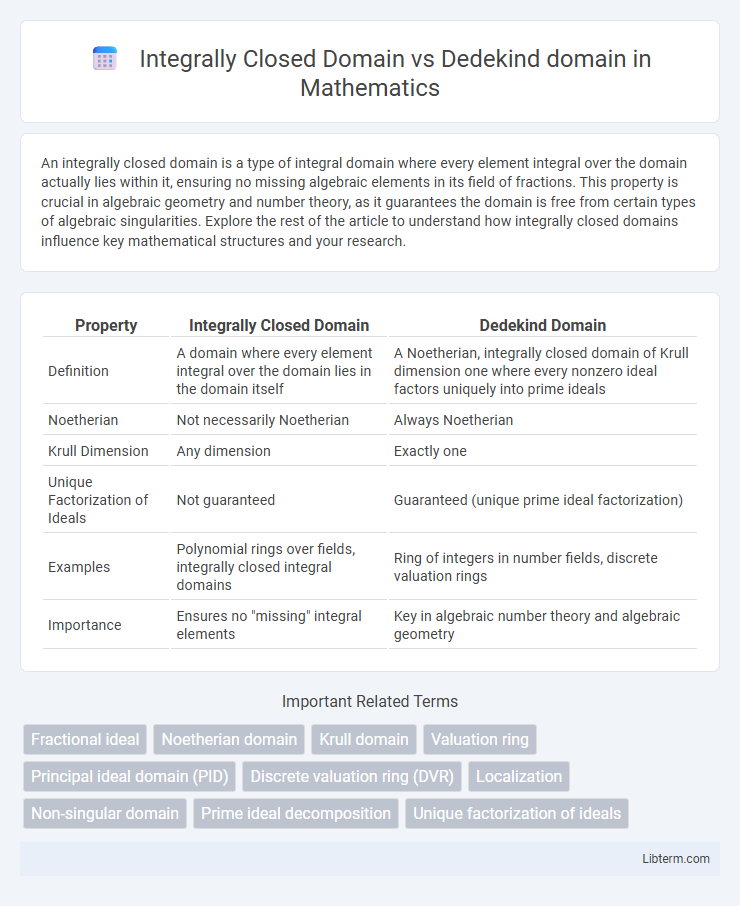
| Property | Integrally Closed Domain | Dedekind Domain |
|---|---|---|
| Definition | A domain where every element integral over the domain lies in the domain itself | A Noetherian, integrally closed domain of Krull dimension one where every nonzero ideal factors uniquely into prime ideals |
| Noetherian | Not necessarily Noetherian | Always Noetherian |
| Krull Dimension | Any dimension | Exactly one |
| Unique Factorization of Ideals | Not guaranteed | Guaranteed (unique prime ideal factorization) |
| Examples | Polynomial rings over fields, integrally closed integral domains | Ring of integers in number fields, discrete valuation rings |
| Importance | Ensures no "missing" integral elements | Key in algebraic number theory and algebraic geometry |
Introduction to Integral Closure in Rings
Integral closure in rings refers to the set of elements in an extension ring that satisfy a monic polynomial with coefficients in the original ring, ensuring integrally closed domains contain all elements integral over them. Dedekind domains are a particular class of integrally closed Noetherian integral domains of Krull dimension one, distinguished by their ideal factorization properties. Understanding integral closure is essential for differentiating integrally closed domains from Dedekind domains, where the latter also requires conditions like Noetherianity and dimension constraints.
Defining Integrally Closed Domains
An integrally closed domain is a commutative ring with unity in which every element integral over the domain actually lies within the domain itself, ensuring no proper integral extensions occur inside its field of fractions. This property characterizes integrally closed domains as those containing all roots of monic polynomials with coefficients in the domain, distinguishing them from general integral domains. Dedekind domains represent a specialized class of integrally closed domains that are Noetherian, integrally closed, and of Krull dimension one, often used in algebraic number theory for their unique factorization of ideals.
Understanding Dedekind Domains
Dedekind domains are a class of integrally closed domains characterized by having every nonzero ideal factor uniquely into prime ideals, which makes them fundamental in algebraic number theory and algebraic geometry. Unlike general integrally closed domains, Dedekind domains are Noetherian, one-dimensional, and integrally closed in their field of fractions, ensuring a robust ideal factorization theory. Understanding Dedekind domains involves studying their unique factorization of ideals rather than elements, distinguishing them from broader integrally closed domains.
Key Properties of Integrally Closed Domains
Integrally closed domains are integral domains in which every element integral over the domain already belongs to it, ensuring no proper integral extensions within their field of fractions. Key properties include stability under localization, preservation of integrality, and characterization by the absence of nontrivial integral extensions within the fraction field. Dedekind domains, being Noetherian integrally closed domains of dimension one where every nonzero ideal factors uniquely into prime ideals, extend integrally closed domains by adding dimensional and ideal-theoretic conditions.
Fundamental Characteristics of Dedekind Domains
A Dedekind domain is an integrally closed Noetherian domain of Krull dimension one where every nonzero prime ideal is maximal, distinguishing it from general integrally closed domains that may lack these properties. Its fundamental characteristics include unique factorization of ideals into prime ideals, ensuring ideal class group finiteness, and the localization at any nonzero prime ideal results in a discrete valuation ring. These properties make Dedekind domains central to algebraic number theory and algebraic geometry, especially in the study of rings of integers in number fields.
Relationship Between Integrally Closed and Dedekind Domains
Dedekind domains are a special class of integrally closed domains characterized by being Noetherian, integrally closed in their field of fractions, and having Krull dimension one. Every Dedekind domain is integrally closed, but not all integrally closed domains are Dedekind domains, as integrally closed domains can have higher dimensions and need not be Noetherian. The key distinction lies in the dimensionality and ideal factorization properties, where Dedekind domains ensure unique factorization of ideals into prime ideals.
Distinguishing Features: Similarities and Differences
Integrally closed domains are integral domains where every element integral over the domain lies within it, ensuring no proper integral extensions exist; Dedekind domains are a special class of integrally closed Noetherian domains of Krull dimension one characterized by unique factorization of ideals into prime ideals. While both domains guarantee integral closure, Dedekind domains extend this property by enforcing Noetherian conditions and dimension constraints, facilitating ideal theory and class group analysis. The key distinction lies in Dedekind domains' restriction to dimension one and Noetherian property, making them suitable for algebraic number theory, whereas integrally closed domains can have arbitrary dimension without necessarily being Noetherian.
Examples of Integrally Closed Domains
Integrally closed domains include important examples such as the ring of integers \(\mathbb{Z}\), polynomial rings over fields like \(k[x]\) where \(k\) is a field, and coordinate rings of nonsingular affine algebraic varieties. Unlike Dedekind domains, which are integrally closed Noetherian domains of dimension one with every nonzero ideal factorizing uniquely into prime ideals, integrally closed domains need not be Noetherian or have dimension one. The integral closure property ensures elements algebraic over the domain actually lie within it, exemplified by \(\mathbb{Z}\) being integrally closed in its field of fractions \(\mathbb{Q}\).
Notable Instances of Dedekind Domains
Dedekind domains represent an important class of integrally closed domains characterized by the property that every nonzero ideal factors uniquely into prime ideals. Notable instances of Dedekind domains include the ring of integers in number fields, such as the ring of Gaussian integers \(\mathbb{Z}[i]\), and the coordinate rings of non-singular algebraic curves over a field. These domains serve as foundational examples in algebraic number theory and algebraic geometry, highlighting their integrally closed nature alongside the unique factorization of ideals.
Applications and Significance in Algebraic Number Theory
Integrally closed domains ensure all elements integral over the domain lie within it, providing a stable ring structure essential for studying algebraic integers. Dedekind domains, as integrally closed Noetherian domains of dimension one, uniquely factorize ideals into prime ideals, enabling precise analysis of algebraic number fields' arithmetic properties. These domains underpin the ring of integers in number fields, facilitating critical applications in class field theory, ideal class groups, and the resolution of Diophantine equations.
Integrally Closed Domain Infographic
 libterm.com
libterm.com